Solución - IES Vega del Jarama
Anuncio
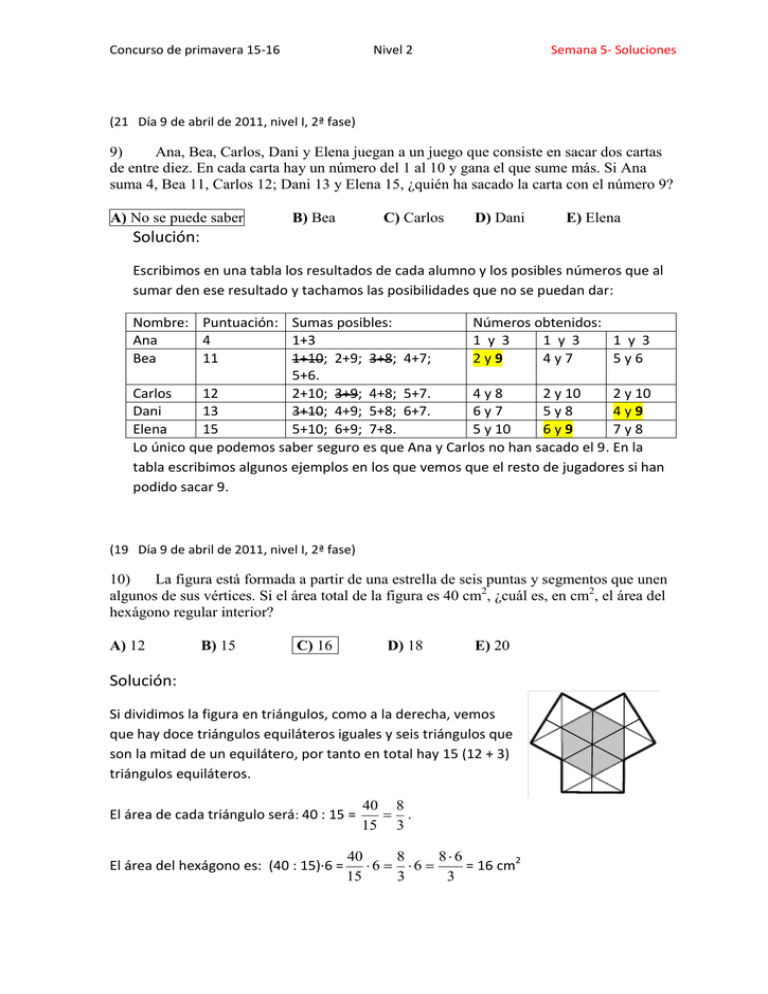
Concurso de primavera 15-16 Nivel 2 Semana 5- Soluciones (21 Día 9 de abril de 2011, nivel I, 2ª fase) 9) Ana, Bea, Carlos, Dani y Elena juegan a un juego que consiste en sacar dos cartas de entre diez. En cada carta hay un número del 1 al 10 y gana el que sume más. Si Ana suma 4, Bea 11, Carlos 12; Dani 13 y Elena 15, ¿quién ha sacado la carta con el número 9? A) No se puede saber B) Bea C) Carlos D) Dani E) Elena Solución: Escribimos en una tabla los resultados de cada alumno y los posibles números que al sumar den ese resultado y tachamos las posibilidades que no se puedan dar: Nombre: Puntuación: Sumas posibles: Números obtenidos: Ana 4 1+3 1 y 3 1 y 3 1 y 3 Bea 11 1+10; 2+9; 3+8; 4+7; 2y9 4y7 5y6 5+6. Carlos 12 2+10; 3+9; 4+8; 5+7. 4y8 2 y 10 2 y 10 Dani 13 3+10; 4+9; 5+8; 6+7. 6y7 5y8 4y9 Elena 15 5+10; 6+9; 7+8. 5 y 10 6y9 7y8 Lo único que podemos saber seguro es que Ana y Carlos no han sacado el 9. En la tabla escribimos algunos ejemplos en los que vemos que el resto de jugadores si han podido sacar 9. (19 Día 9 de abril de 2011, nivel I, 2ª fase) 10) La figura está formada a partir de una estrella de seis puntas y segmentos que unen algunos de sus vértices. Si el área total de la figura es 40 cm2, ¿cuál es, en cm2, el área del hexágono regular interior? A) 12 B) 15 C) 16 D) 18 E) 20 Solución: Si dividimos la figura en triángulos, como a la derecha, vemos que hay doce triángulos equiláteros iguales y seis triángulos que son la mitad de un equilátero, por tanto en total hay 15 (12 + 3) triángulos equiláteros. El área de cada triángulo será: 40 : 15 = El área del hexágono es: (40 : 15)·6 = 40 8 . 15 3 40 8 86 6 6 = 16 cm2 15 3 3