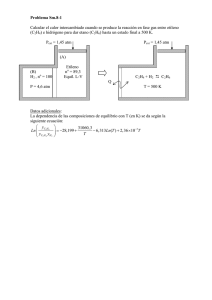
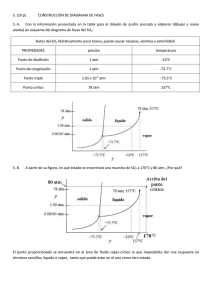
Gases Ideales I

Gases Ideales 1
1
Atmósfera
Componentes mayoritarios aire seco
(% peso)
N 2 78%
Además:
CO2
H2O (vapor)
O 2 21%
Ar 0.93%
Otros 0.04%
Otros gases inertes : He, Ne, Kr, Xe
2
GAS
Estado gaseoso a temperaturas y presiones ordinarias.
11 elementos
He, Ne, Ar, Kr, Xe, Rn,
H2, N2, O2, O3, F2, Cl2
l
Compuestos moleculares:
CO, CO2, HCl, NH3, CH4, NO, NO2, N2O,SO2, SO3, HCN.
l
VAPOR
forma gaseosa de cualquier sustancia que es líquida ó sólida a
temperaturas y presiones ordinarias.
3
Volumen
(sólido, líquido, gas)
depende de
§ Temperatura (T)
§ Presión (P)
Ecuación de estado:
V = V (T, P, n)
Liquídos y sólidos
Ecuación de estado muy complicadas y difieren
considerablemente de una sustancia a otra.
4
Gases
Ecuación de estado universal.
moléculas casi independientes unas de otras
la naturaleza particular no afecta el comportamiento
general
•
•
•
•
se pueden comprimir
ocupan todo el espacio disponible
MOLÉCULAS
•
•
Separadas
Movimiento caótico
5
Presión atmosférica
6
Barómetro
Presión atmosférica:
Presión ejercida por una
columna de Hg
de 76 cm de longitud
y de densidad
13,5951 g/cm3
en un lugar en donde g
es 980,665 cm/s2
7
Unidades
F
P =
A
P = hδ g
1 Pa = 1 N/m2
1 atm = 760 mmHg
= 760 torr
1 atm = 101325 Pa
= 1.013 x 105 Pa
= 1.013 x 102 kPa
8
Ejercicio
Calcular la equivalencia entre una atmósfera estándar y
Pa. Recordar que una atm es la presión ejercida por una
columna de Hg de 76 cm de longitud y de densidad
13,5951 g/cm3 en un lugar en donde g es 980,665
cm/s2
F
P =
A
9
Presión de un gas
Caso A
Pgas = Pext
Caso B
Pgas = Pext + ∆h
Caso C
Pgas = Pext - ∆h
10
Ecuación de estado:
V = V (T, P, n)
LEYES DE LOS GASES
LEY DE BOYLE-MARIOTTE (T constante)
LEY DE CHARLES (V constante)
LEY DE GAY-LUSSAC (P constante)
LEY DE AVOGADRO (T y P constantes)
11
LEY DE BOYLE-MARIOTTE
TEMPERATURA
CONSTANTE
12
Ley de Boyle-Mariotte. (T constante)
Para una T y m
dada,
P α 1/V
P x V = cte
13
Ley de Boyle-Mariotte. (T constante)
Para una T y m
dada,
P α 1/V
P x V = cte
14
LEY DE BOYLE-MARIOTTE
p = constante / V
TEMPERATURA
CONSTANTE
ISOTERMAS
15
LEY DE BOYLE-MARIOTTE
TEMPERATURA
CONSTANTE
Ejercicios
1.- Una masa dada de gas ocupa un volumen de 240 ml a
1.25 atm, ¿cuál será el cambio de volumen si la presión se
llevara a 0.75 atm a la misma T?
2.- Un globo inflado tiene un volumen de 0.55 l al nivel del
mar (1 atm) y se deja elevar a una altura de 6.5 km,
donde la presión es de unos 0.40 atm. Considerando que
la temperatura permanece constante, ¿cuál es el volumen
final del globo?
16
LEY DE CHARLES
P atm
PRESIÓN
CONSTANTE
P atm
Termómetro
aire
Vo
100 OC
0 OC
Termómetro
V100
Vt
17
Ley de Charles. (P constante)
Para una P y m dada:
V aumenta linealmente
con t (°C)
V = Vo + Vo α t
α = 1 / 273 ºC-1
18
Ley de Charles. (P constante)
Isobaras
V = Vo + Vo α t
α = 1 / 273 ºC-1
V = cte. T (K)
19
LEY DE CHARLES
PRESIÓN
CONSTANTE
20
LEY DE CHARLES
PRESIÓN
CONSTANTE
Escala absoluta de temperatura:
T (K), el 0 K es la temperatura más baja posible ya que
el gas tendría V = 0 a esa temperatura, y cualquier
temperatura menor a 0 K correspondería a V < 0.
21
LEY DE GAY-LUSSAC
VOLUMEN
CONSTANTE
P = constante × T
22
LEY DE GAY-LUSSAC
VOLUMEN
CONSTANTE
ISOCORAS
23
Leyes de los Gases: Ley de Avogadro
ØHipótesis de Avogadro: volúmenes iguales
de gases a la misma temperatura y presión
contienen el mismo número de moléculas.
ØLey de Avogadro: el volumen de gas a una
cierta
temperatura
y
presión
es
directamente proporcional al número de
moles de gas.
V = constante × n
24
LEY DE AVOGADRO
VOLÚMENES MOLARES a 0OC y 1 atm
PRESIÓN
Y
TEMPERATURA
CONSTANTES
EL VOLUMEN DE
GAS ES
DIRECTAMENTE
PROPORCIONAL
AL NÚMERO DE
MOLÉCULAS
25
GAS IDEAL
CUMPLE CON LAS LEYES DE LOS GASES EN
TODO INTERVALO DE PRESIÓN Y
TEMPERATURA
LEY DE BOYLE-MARIOTTE (T constante)
P V = cte1
LEY DE CHARLES (P constante)
V / T = cte2
LEY DE GAY-LUSSAC (V constante)
P / T = cte3
LEY DE AVOGADRO (T y P constantes)
V / n = cte4
26
Ecuación general de estado de los gases
ideales
Resumen de Leyes de los Gases:
Boyle:
V ∝ 1 / P (constante n, T)
Charles:
V∝T
(constante n, P)
Gay-Lussac: P ∝ T
(constante n, V)
Avogadro: V ∝ n
(constante P, T)
 nT 
V = R 
 P 
PV= nRT
27
Ley del gas ideal
Ecuación de estado del gas ideal
PV=nRT
Valores de R
8.314 107 erg / K mol
Constante
de los gases
8.314 J / K mol
1.987 cal / K mol
0,082 l atm / K mol
28
CPTA: Condiciones de Presión y Temperatura Ambiente
25,00 °C y 1 bar (106 barias)
CNTP: Condiciones Normales de Temperatura y Presión
0 °C y 1 atm
29
DENSIDAD DE LOS GASES
30
DENSIDAD DE LOS GASES IDEALES
m
δ =
V
pV
= nR
T
M ×P
δ =
RT
31
DENSIDAD DE LOS GASES
M ×P
δ =
RT
32
Ejercicio
El compuesto volátil geraniol, un componente del aceite de
las rosas, se usa en perfumería. La densidad del vapor a
260 °C y 103 torr es 0.480 g l-1. ¿Cuál es la masa molar
del geraniol?
1. Ordenar los datos y verificar las unidades
2. Despejar M y calcular
33
Mezclas de gases : LEY DE DALTON
Presión parcial : presión individual del componente
gaseoso en la mezcla de gases.
• Es la presión que ejercería el gas si estuviera solo,
ocupando todo el volumen del recipiente a la misma T que la
mezcla.
Ley de las presiones parciales de Dalton: la presión total
de una mezcla de gases es la suma de las presiones
parciales.
34
LEY DE DALTON DE LAS PRESIONES
PARCIALES
Presió
Presión total
P = P1 + P2 + P3 + .......
Presiones parciales
P1, n1
(P1 + P2), n
P2, n2
T y V constantes
35
LEY DE DALTON
nB RT
PB =
V
n A RT
PA =
V
PRESIONES
PARCIALES
RT
RT
P = ( nA + nB )
=n
V
V
RT
RT
P = nA
+ nB
= PA + PB
V
V
PA n A
=
= xA
P
n
Fracción molar de A
PB n B
=
= xB
P
n
x A + xB = 1
Fracción molar de B
36
Ejercicio
Una muestra de aire seco de masa total 1.00 g consiste casi
exclusivamente de 0.76 g de nitrógeno y de 0.24 g de
oxígeno. Calcular las presiones parciales de los gases de los
gases.
1.
2.
3.
4.
5.
Calcular la cantidad de cada gas en moles.
Calcular los moles totales.
Calcular las fracciones molares.
Calcular las presiones parciales tomando P = 1 atm.
Verificar la respuesta.
37
Teoría cinética de los gases ideales
• Los gases están formados por un gran número de moléculas
que se mueven de modo continuo y aleatorio.
• El volumen de estas partículas es despreciable frente al
volumen del recipiente.
• Las fuerzas de atracción y repulsión entre las moléculas del
gas son insignificantes.
• Las moléculas chocan entre sí y con la paredes del recipiente
en forma elástica.
• La energía cinética media de las moléculas no cambia en el
tiempo, en tanto la temperatura del gas permanezca constante.
• La energía cinética media de las moléculas es proporcional a la
temperatura absoluta. A cualquier temperatura dada, las
moléculas de todos los gases tienen igual energía cinética.
38