Tema 4: VARIABLE ALEATORIA N

Tema 4: VARIABLE
ALEATORIA N-DIMENSIONAL
Carlos Alberola López
Lab. Procesado de Imagen, ETSI Telecomunicación
Despacho 2D014
caralb@tel.uva.es, jcasasec@tel.uva.es,
http://www.lpi.tel.uva.es/sar
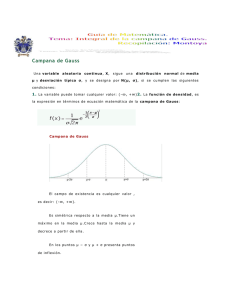
Concepto de VA N-dimensional
X
(X, Y )
Y
Extensión a
composición de N
experimentos ε i
X = (X1 , X 2 ,L, X N )
Conceptos básicos
•
Función de distribución: se define como la probabilidad de la
intersección de N sucesos:
I
•
Función de densidad
•
Cálculo de una probabilidad en espacio N-dimensional
Conceptos básicos
•
•
Reducción del número de variables en las funciones:
•
Función de distribución: evaluar en infinito las variables a
eliminar
•
Función de densidad: integrar en el recorrido de las variables
a eliminar
Independencia de variables: factorización de funciones de
caracterización
Conceptos básicos
•
N funciones de N VAs: Teorema fundamental:
•
Si partimos de una situación del tipo:
Y1
Y2
= g 2 (X1 , X 2 ,L, X N )
M
M
YN
•
= g1 (X1 , X 2 ,L, X N )
= g N (X1 , X 2 ,L, X N )
Podemos caracterizar la VA de salida mediante:
Conceptos básicos
•
Respecto de funciones condicionadas:
•
Recordemos la relación vista en el caso 2D:
•
Y recordemos la regla de la cadena para probabilidades
condicionadas
•
O bien
Conceptos básicos
•
Teniendo esto presente, podemos escribir:
•
O bien
f ( x1 , x2 ,L, x N ) = f (x1 , x2 x3 ,L, x N ) f ( x3 ,L, x N )
•
Existen pues múltiples posibilidades
Conceptos básicos
•Y siguiendo esta pauta es sencillo eliminar la
dependencia de variables en las funciones
condicionadas:
•Variables a la izquierda del condicionante:
integrar con respecto a ellas.
•Variables a la derecha del condicionante:
multiplicar por la función de densidad de esa
variable condicionada a las demás e integrar
con respecto a ella.
Conceptos básicos
•Estimación de mínimo error cuadrático medio:
•El estimador lineal se obtiene resolviendo un
problema de optimización.
•El estimador no lineal es la extensión del
resultado visto en el capítulo anterior, es decir,
la esperanza de la variable a estimar
condicionada a las observaciones:
Esperanzas matemáticas
•Los conceptos de correlación y covarianza siguen estando
presentes. Tales parámetros miden la relación cruzada entre dos
variables (no entre tres o más).
•Cuando se tienen N variables hay que especificar entre qué dos
variables (de las N) se están especificando tales parámetros.
•Es cómodo emplear operadores vectoriales y/o matriciales para
ordenar esta información.
Vector de medias:
Matriz de covarianza:
Esperanzas matemáticas
•La ortogonalidad y/o la incorrelación son propiedades cómodas
para cálculos de esperanzas en las que haya N variables
N
involucradas. Por ejemplo, sea
Z = ∑ X i. Su varianza es:
i =1
Esperanzas matemáticas
•Entonces:
{
E (Z − ηZ )
2
}
Variables complejas
•Las variables complejas son una combinación lineal de variables
Z = X + jY
reales:
•Por tanto:
E {Z} = E {X + jY} = E{X}+ jE{Y}
•Respecto de la varianza, en el caso complejo tenemos que
encontrar un radio de dispersión. Por ello se define:
Valor cuadrático medio
Variables complejas
•La esperanza de una función de la variable compleja puede
escribirse como hemos visto para el caso de una función de 2
variables aleatorias:
•Independencia: si dos variables complejas son independientes, las
componentes cartesianas son independientes entre sí:
Z1
= X1 + jY1
Z2
= X 2 + jY2
independientes
Variables complejas
•Al respecto de correlación y covarianza:
•El orden de las variables por tanto ahora es importante:
Teoremas asintóticos
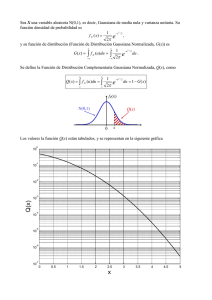
•Teorema del Límite Central: la suma de variables
independientes e indénticamente distribuidas (IID) tiende a tener
una distribución gaussiana.
con
•El teorema también es cierto cuando de las VAs son
independientes y tienen distribuciones similares.
Teoremas asintóticos
•Para VAs continuas y para VAs discretas con valores
equiespaciados también se observa que:
con
Teoremas asintóticos
X1 + X 2
X1
5
∑X
i =1
X i ~ U (0,1)
10
i
∑X
i =1
i
Teoremas asintóticos
•Teorema de Demoivre-Laplace: caso particular del Teorema del
Límite Central para el caso de VAs de Bernouilli IID:
N >> 1
⎧0 P (X i = 0 ) = q
Xi = ⎨
⎩1 P (X i = 1) = p
X ~ B(N, p )
con
2
Teoremas asintóticos
•Ley de los Grandes Números: convergencia de la frecuencia
relativa a la probabilidad axiomática. Formalmente:
•con
f r ( A) =
P ( A)
NA
N
=p
Teoremas asintóticos
•Ley de los Grandes Números. Demostración:
Demoivre-Laplace
Teoremas asintóticos
•Por tanto:
• La expresión
sirve para hallar el valor de N que hace falta para caer dentro de
un intervalo del valor p con una probabilidad deseada.
Variables conjuntamente gaussianas
•N VAs son conjuntamente gaussianas si la función de densidad
de las mismas se puede escribir
1xN
Nx1
NxN
1x1
Variables conjuntamente gaussianas
•Si N VAs son conjuntamente gaussianas:
•Que cada una de ellas es marginalmente gaussiana, con los
parámetros (media y varianza) según indica el vector de medias
y la matriz de covarianza.
•Que cada subconjunto de k<N variables son conjuntamente
gaussianas.
•Que la función de densidad de k variables condicionadas a las
N-k restantes es la correspondiente a una variable
conjuntamente gaussiana.
Variables conjuntamente gaussianas
•IMPORTANTE: La transformación lineal de VAs conjuntamente
gaussianas es conjuntamente. gaussiana!!!!!
•Partimos de Y = A X
donde la matriz de transformación es
de rango completo. Entonces, aplicando el teorema fundamental:
•Operando y agrupando términos matriciales en la matriz
llega fácilmente al resultado
C
se
Variables conjuntamente gaussianas
•Si N VAs son conjuntamente gaussianas:
•Incorrelación implica independencia
σ
CX =
2
X1
0
M
0
0
σ
2
X2
0
L
L
0
0
M
O
0
0
σ
2
XN
Gaussiana Bivariante
•Particularización de lo anterior para N=2. La función de densidad
resulta ser:
•Si ρ XY = 0 entonces los términos cruzados desaparecen y la
función de densidad se factoriza en el producto de las marginales
(luego, de nuevo, incorrelación implica independencia)
b) Las variables son gaussianas correladas. Por ello la variable
bidimensional es una gaussiana bivariante. Nos piden:
fY (y x )
E {Y x}
Para ello
1
⎡ x 2 2 ρxy y 2 ⎤ x 2
1
−
− 2 + 2⎥
2 ⎢ 2
σ
σ ⎦⎥ 2σ 2
2 1− ρ ⎣⎢ σ
f XY ( x, y ) 2πσ 2 1 − ρ 2
(
fY (y x ) =
=
e
1
f X (x )
σ 2π
)
e
Introduciendo el segundo factor:
fY (y x ) =
resulta
fY
1
−
2 1− ρ 2
(
e
1
σ 2π (1 − ρ 2 )
(y x ) =
1
σ 2π (1 − ρ
2
)
)
(
)
⎡ x 2 x 2 1− ρ 2 2 ρxy y 2 ⎤
− 2 + 2⎥
⎢ 2−
2
σ
σ
σ ⎥⎦
⎢⎣ σ
1
−
2 1− ρ 2
(
e
)
⎡ ρ 2 x 2 2 ρxy y 2 ⎤
⎢ 2 − 2 + 2⎥
σ
σ ⎥⎦
⎢⎣ σ
es decir
fY (y x ) =
1
σ (1 − ρ
2
)
1
−
2 1− ρ 2
2π
Según enunciado
(
e
)
( y − ρx )2
σ2
(
Y X = x 0 ~ N ρx 0 , σ 1 - ρ 2
)
P (R ) = ∫ f XY ( x, y )dxdy
Solución: a)
R
2
⎛ 1 ⎞
= ∫⎜
⎟ e
R ⎝ σ 2π ⎠
x2
− 2
2σ
e
y2
− 2
2σ
dxdy
Si ahora hacemos
P (R ) = ∫
∫
2
⎛ 1 ⎞
⎜
⎟ e
⎝ σ 2π ⎠
= r cos(θ )
y
= r sin (θ )
Nos queda
R
1
2π
4
0 0
x
r2
− 2
2σ
rdrdθ = ∫
2π
0
1
4
0
1
r
dθ ∫ 2 e
2π
σ
r2
− 2
2σ
dr
P (R ) = ∫
2π
0
1
4
0
r
1
dθ ∫ 2 e
σ
2π
r2
− 2
2σ
dr = − e
P (R ) = 1 − e
1
32σ 2
= 1− e
0
Si ha de verificarse que:
−
r2
− 2
2σ
1
4
≥ 0.7
entonces, despejando tenemos
σ ≤ 0.1611
−
1
32σ 2