polinomios - Colegio Sagrado Corazón de Linares
Anuncio

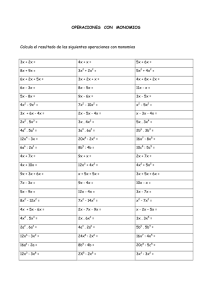
4º E.S.O. Colegio Sagrado Corazón DPTO. DE MATEMATICAS POLINOMIOS 1. Realiza las siguientes divisiones de polinomios: a) (2x4 – 5x³ + 3x² - 6x + 7) : (x² – 5x + 1) b) (x³ - 2x² + 3x - 1) : (x² + 3x - 1) c) (12x4 - 2x² + 5) : (x² – 2x - 1) d) (3x4 - 2x + 1) : (x² + 2) e) (6x4 + 5x³ - 7x² + 3x + 2) : (2x² + 3x - 1) f) (x4 - 6x³ + 2x² + 3x - 4) : (x² + x + 2) g) (8x4 - 2x³ + 5x - 3) : (2x² + x - 1) 2. Halla el valor de m en el polinomio x³-15x+m si su valor numérico es 8 para x = - 4. 3. Aplica el método de Ruffini para hacer las siguientes divisiones: a) (5x4 – 2x + 1) : (x – 2) b) (3x6 + 2) : (x + 1) 4 c) (5x – 3x² + 6x - 1) : (x – 1) 4. Factoriza los polinomios: a) P(x) = x4 – 7x³ + 5x² + 31x – 30 b) Q(x) = x4 + 2x³ - 3x² - 4x + 4 c) R(x) = x³ - x² - 6x d) S(x) = 2x6 – 8x5 + 32x³ - 32x² e) T(x) = 2x³ - 11x² + 2x + 15 f) U(x) = 3x4 – 6x³ - 3x² + 6x g) V(x) = x³ - 2x² + x –2 h) W(x) = 2x5 - 32x i) A(x) = x4 - x³ - 3x² + 5x – 2 j) B(x) = x4 + 6x³ + 12x² +8x k) C(x) = x³ - 2x² - x + 2 l) D(x) = x³ - 7x – 6 m) E(x) = 2x³ - 3x² - 5x + 6 n) F(x) = x³ + 2x² - x - 2 o) G(x) = x4 - 5x² + 4 p) H(x) = x4 - 9x² q) I(x) = x 4 + x³ - 9x² - 9x r) J(x) = x³ + 5x² + x + 5 s) K(x) = x³ + x² - 8x - 12 t) L(x) = 2x³ - 3x² - 32x -15 u) M(x) = x³ + 3x² - 4x - 12 v) N(x) = x 4 - 16x² w) Ñ(x) = x³ - 21x - 20 x) O(x) = x³ + 9x² + 14x y) P(x) = x³ + 8x² +5x - 14 z) P(x) = x4 - 16 aa) P(x) = x³ + 3x² -13x - 15 bb) P(x) = x³ + 8 cc) P(x) = x5 - 27x² dd) P(x) = x4 - x³ - 4x² + 4x ee) P(x) = x³ - 2x² +x -2 5. Calcula el m.c.d. y el m.c.m. de: a) P(x) = x² - 3x; Q(x) = x² - 5x + 6. b) P(x) = 2x² - 8x + 8; Q(x) = 5x – 10; y R(x) = 10x² - 40. c) P(x) = x³ - 2x² - x + 2; Q(x) = 2x² - 6x + 4; y R(x) = 5x³ - 15x² + 10x. 1 4º E.S.O. Colegio Sagrado Corazón DPTO. DE MATEMATICAS 6. Simplifica las siguientes fracciones polinómicas: x3 −1 x2 + 4x + 3 = h) a) x 2 −1 x2 − x − 6 8 x 2 + 16 x x 3 + 3x 2 + 3x + 1 b) i) = = 6 x 2 − 24 x3 + x2 − x −1 x 5 − 3x 2 2x 2 − 5x − 3 = = c) j) 2 x 3 − 5x 2 x 2 + 4 x − 21 x3 − x2 − 2x x2 − 4 d) k) = = x3 − x x 2 − 3 x − 10 x 3 + x 2 − 5x − 5 4 x 2 + 12 x + 9 e) l) = = 2 x 2 + 3x x 3 + x 2 − 3x − 3 x 3 − 3x 2 2x3 − 6x = = m) f) x 3 + x 2 − 3x − 3 x3 − 9x x2 + 4x − 5 x2 − 6x + 9 = = n) 2 g) 2 x + 7 x + 10 x − 9 x + 18 7. Efectúa las siguientes operaciones, simplificando el resultado siempre que sea posible: 2 x − 1 3x + 1 1 − x x2 +1 x + 2 a) = − 2 + n) + = x −1 x + 1 x −1 x + 1 x 2 −1 3x − 1 x − 5 x2 x 2 + 2 x + 1 35 + = b) o) ⋅ ⋅ = x −3 x + 2 5( x + 1) 7x 2x 2x 2x + 3 c) + 2 = x 2 −1 x +1 = ÷ p) 2 x−2 x +4 x + 4x + 4 x + 2 2x 2x + 3 + 2 = d) x −1 2x x +1 1 ⋅ ⋅ ⋅ = q) x−2 x −4 x2 x 2 −1 x 2 3x − 1 2x + 3 = : 2 e) 3x + 6 5x + 5 2 r) ÷ = x + x−2 x − x−6 x +1 x2 −1 x + 5 x −1 + = f) x + 5 x 2 − 25 2 x − 2 3x s) ÷ = 2 x x x−2 x +1 ⋅ 2 = g) 2 1 1 x −1 x − 4x + 4 t) x − ÷ = x x 1 1 1 h) 3 + 2 − ⋅ x 3 + x 2 = 2 2 x x x u) 2 x − 2 ÷ 2 = x x x +1 x −1 5 x i) + ⋅ + − x = 1 1 2 x − 1 x + 1 3x 3 v) + − 2 = 1 1 1 x x x + − − x x j) x − = ÷ x + x − 1 5( x − 1) ÷ = w) x +1 x +1 3 3x 2 1 1 2x k) 1 − ⋅ 2 − x2 − 9 x2 − 6x + 9 = x) ÷ = x x −1 x + 1 x2 + 9 x 4 − 81 2 5x + 2 = l) x x2 −1 y) + = 3x − 3 x − 1 2 x x 5 10 4 − + x x2 −1 + 2 = m) 5 x + 10 x − 4 ( ) 2