Descarga
Anuncio

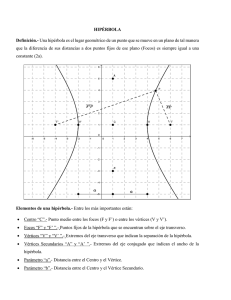
RESUMEN DE SECCIONES CÓNICAS. Por: Carlos Alberto Ríos Villa Círculo Elipse (h) Parábola (h) Hipérbola (h) Elipse (v) Parábola (v) Hipérbola (v) Definición: Una sección cónica es la intersección de un plano y un cono. Círculo Definición: es el conjunto de todos los puntos que cumple la condición... la distancia a un punto fijo (centro) es constante Elipse la suma del las distancias a los foco es constante Parábola Hipérbola la distancia al la diferencia foco = la entre las distancia a la distancias a cada directriz foco es constante a = 1/2 la longitud del eje (h,k): centro mayor a = el radio b = 1/2 la mayor (= 1/2 la longitud del eje longitud del eje menor mayor) c = la distancia b = el radio desde el centro menor (= 1/2 la al foco longitud del eje menor) c = la distancia desde el vértice al foco. Variables: p = la distancia desde el vértice Excentricidad: al foco (o a la Se refiera a que directriz) tan alargada o r = el radio del e= excentricidad (h,k): vértice círculo indica que tan (h,k): centro (h,k): centro puntiaguda es la hipérbola. Si la redondeada o tan Directriz: recta excentricidad es alargada es la de lacual grande los focos elipse.Si e se equidistan todos están cerca del acerca a cero la los puntos con centro y las elipse tiende a respecto al foco ramas de la redondearse y si hipérbola son casi se acerca a 1 rectas verticales. tiende a Si la alargarse. 0 < e excentricidad es < 1, si e=0 será cercana a uno los una focos están lejos circunferencia, si del centro y las e=1 será una ramas de la recta hipérbola son más puntiagudas. Circunferencia Desde la ecuación Desde la ecuación canónica general (X-h)2 + (y-k)2 = r2 x2+y2+Dx+Ey+F=0 Centro: C(h,k). Radio: r Nota: recuerde que el signo menos de la ecuación cambia el h D ; 2 k E 2 r h2 k 2 F signo de h y k Centro: C(h,K) (x-3)2+(y+2)2=36 x2-2-6x+9+y2+4y+4=36 C(3,-2); r=6 x2+y2-6x+4y-23=0 D=-6; E=4; F= - 23 h=-(-6)/2=3; k=4/2=-2 ejemplo C(3,-2) r= (3)2 (2)2 (23) = 36 r = 6 Elipse Horizontal: (x-h)2 (y-k)2 1; a2 b2 Ax2+By2+Dx+Ey+F=0; a > b con A<B Centro: C(h,k) A = b2 Eje mayor = 2a B = a2 Eje menor = 2b D = -2b2h c2 = a2- b2 Focos: X1=(h-c , k) X2=(h+c,k) Vértices: V1=(h-a , k) E = -2a2k F = b2h2 + a2k2 - a2b2 Lado recto=2b2/a V2=(h+a , k) B1=(h , k-b) B2=(h , k+b) Excentricidad; e=c/a 2 Lado recto=2b /a (x 3)2 (y 3)2 1 9 4 a2=9 a=3 b2=4 b=2 C(-3,3) Realizando las operaciones, mínimo h=-3, C2=9-4=5 k=3 C=√5=2.24 Focos: X1=(-3-2.24,3)=(5.24,3) Ejemplo x 2 6x 9 y 2 6y 9 1 9 4 X2=(-3+2.24,3)=(-0.76;3) Vértices: V1=(3-3 , 3)=(0,3) común denominador y simplificando se obtiene la ecuación general: 4x2+9y2+24x-54y+81=0 A=4 ; B=9 ; D=24 ; E=-54 ; F=81 4=b2 b=2; 9=a2 a=3 24=-2x22 x h despejando h=-3 V2=(3+3 , 3)=(6,3) -54=-2x32k B1=(3 , 3-2)=(3,1) De igual forma que para la canónica B2=(3 , 3+2)=(3,5) Excentricidad: e =√5/3=0.75 Lado recto LR=2b2/a = 2 x 4/2 = 4 despejando k=3 encontramos los focos y los vértices. Elipse Vertical: (x-h)2 (y-k)2 1; b2 a2 a > b Ax2+By2+Dx+Ey+F=0; A>B Centro: C(h,k) A = a2 Eje mayor = 2a C = b2 Eje menor = 2b 2 2 con D = -2a2h 2 c = a - b Focos: F1=(h , k-c) F2=(h , k+c) E = -2b2k F = a2h2 + b2k2 - a2b2 Vértices: W1=(h-b , k); W2=(h+b , k) Lado recto=2b2/a V1=(h , k-a) V2=(h , k+a) Excentricidad; e=c/a 2 Lado recto=2b /a (x 1)2 (y 2)2 1 9 25 x 2 2x 1 y 2 4x 4 1 9 16 a2=25 a=5 Realizando las operaciones, mínimo b2=9 b=3 C(1,-2) h=1 2 C =25-9=16 común denominador y simplificando se obtiene la ecuación general: K=-2 C=4 Focos: Ejemplo F1=(1 , -2-4) F2=(1 , -2+4) Vértices: W1=(1-3 , -2)=(-1,-2) W2=(1+3 ,-2) =(4,-2) V1=(1 , -2-5) = (1,-7) V2=(1 , -2+5) = (1, 3) Excentricidad; e=4/5=0.8 Lado recto LR=2b2/2=2 x 9/2 = 9 25x2+9y2-50x+36y-164=1 A=25 ; B= 9; D=-50 ; E=36 ; F= -164 25=b2 5=b 9=a2 3=a D=-2b2h -50=-2x 25x h luego h= 1 E=-2a2k 36=-2 x 9 x k luego k=-2 De igual forma que con la ecuación canónica se encuentran los focos y los vértices. Hipérbola horizontal (x-h)2 (y-k)2 1 a2 b2 Ax2+By2+Dx+Ey+F=0 Centro: C(h,k) A = b2 Vértices: B = -a2 V1x=(h-a,k) V2x=(h+a,k) D = -2a2h c2= b2+a2 E = 2b2k Focos: F = b2h2 - a2k2 - a2b2 F1=(h-c,k) F2(h+c,k) Lado recto=2b2/a Asíntotas: Excentricidad: E=c/a 2 Lado recto=2b /a (x 1)2 (y 2)2 1 1 4 2 2 h=1; k= -2; a =1 a=1; b =4 b=2 Vértices: V1x=(1-1,-2)=(0,-2) V2x=(1+1,-2)=(2,2) c2= 12+22 Ejemplo c=√5=2.23 (x 2 2x 1) (y 2 4y 2)2 1 1 4 4(x 2 2x 1) (y 2 4y 2) 1 4 Realizando las operaciones algebraicas se obtiene la expresión: 4x2-y2-8x-4y-4=0 Focos: A=4; B=1; D=-8; E=-4; F=-4 F1=(1-2.23,-2) =(1.23,-2) F2(1+2.23,-2=(3.23,-2)) a =A=4 a=2 b2=B=1 b=1 Asíntotas: 2 -8=-2 x 22 x h -4=2 x 12 k h=1 k=-2 De igual manera que con la ecuación canónica se encuentran los demás parámetros. Y=-2±2(x-1) Excentricidad: E=√5/1=√5 2 Lado recto=2 x 2 /1=8 Hipérbola Vertical (y-k)2 (x-h)2 1 2 2 a b Ax2+By2+Dx+Ey+F=0 Centro: C(h,k) A = -a2 Vértices: B = b2 V1y=(h,k-a) V2x=(h,k+a) c2= b2+a2 D = 2a2h E = -2b2k Focos: F = b2k2 - a2h2 - a2b2 F1=(h,k-c) F2(h,k+c) Asíntotas: b x h (y k ) a b x h (y k ) a Excentricidad: e =c/a ; 2 Lado recto=2b /a (y 3)2 (x 2)2 1 9 4 2 =9 a=3 b2=4 b=2 h=2 k=-3 a (y 2 6y 9) (x 2 4x 4)2 1 9 4 4(x 2 2x 1) 9(y 2 4y 2) 1 36 Efectuando las operaciones algebraicas respectivas se obtiene la ecuación: Centro: C(2,-3) 2 2 4y -9x +24y+36x-36=0 Vértices: V1y = (2,-3-3) = (2,-3) Ejemplo 3 V2x = (2,-3+3) = (2,0) c2= 32+22=9+4=√13=3.6 A=-9; B=4; D=36; E= 24; F=-36 -9=-a 2 a=3; 36 = 2 x 32h 4=b2 b=2 h=2 Focos: 24 = -2 x 22k F1=(2,-3—3.6)=(2,-6.6) F2=(2,-3+3.6) =(2,0.6) Con estos datos se Asíntotas: k=-3 establecen los demás parámetros de igual forma X=2±2/3(y+3) que con la ecuación Excentricidad: canónica. e=√13/3=1.2 2 Lado recto=2 x 2 /3 = 8/3 Parábola horizontal (y 2 - k) = 4 p(x -h) 2 y + Dx + Ey + F = 0 Si 4p>0 abre a derecha Si 4p<0 abre a izquierda Vertice: V(h,k) Foco: Si abre a Derecha: F(h+p , k) Si abre a Izquierda: F(h-p , k) D E D E F = -4 p = -2k =-2h =-4 p =k2 +4 ph Directriz: Si abre a derecha: X = h – p Si abre a Izquierda: X = h + p Lado recto LR = │4 p│ Eje focal Y=k Y2-4y+4=8x-24 h = 3; k = 2; 4p = 8 p=2 Como 4P > 0 abre a la derecha D=-8 -8=-4p; p=2 Vértice: V(h,k) = (3,2) E= -4 -4=-2k; k=2 Foco: F(h - p,k) = (3-2,2) = F = 28 28 = 22 + 8h; h=3 (1,2) Ejemplo Y2-4y-8x+28=0 h-p = 3-2 =1 La directriz es: entonces: x=1 Eje focal: y = k osea: y = 2 Lado recto LR= 8 Con estos datos encontramos los demás parámetros de igual forma que con la ecuación canónica Parábola vertical (x - h)2= 4 p(y - k) 2 x + Dx + Ey + F = 0 donde: Vértice V(h,k)) D =-2h E =-4 p F =h2 +4 pk Foco: Si abre arriba F(h , k+p) Si abre abajo F(h , k-p) Directriz: Si abre arriba Y=k + p Si abre abajo Y=k - p Eje focal: X = h Lado recto LR = │4 p│ x2-6x+9=8y-16 h = 3; k= 2 ; x2-6x-8y+25=0 4p = 8 p=2 D = -6; E = -8; F = 25 Como 4p>0 abre hacia arriba. Foco: F(h,k+p)=(3,2+2) = (3,4) Ejemplo Directriz: y = k+p =2+2 entonces la directriz es y = 4 Eje focal: x = h osea: Lado recto: LR = 4p = 8 x = 3 -6 = -2h -8 = -4p h = 3 p = 2 F =h2 +4 pk 25 = 32 + 8k; k = 2 Con estos datos encontramos los demás parámetros de igual forma que con la ecuación canónica