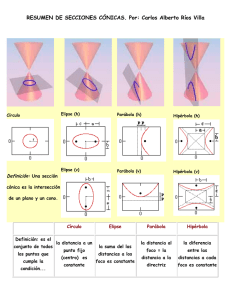
Hipérbola con centro en el origen
Anuncio
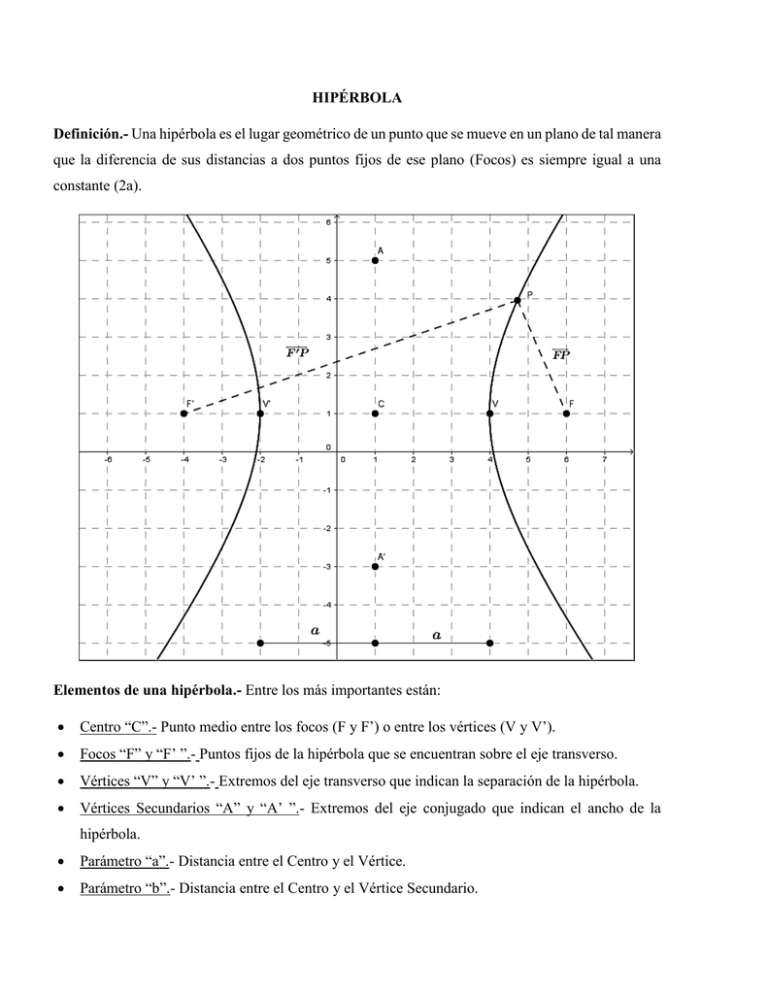
HIPÉRBOLA Definición.- Una hipérbola es el lugar geométrico de un punto que se mueve en un plano de tal manera que la diferencia de sus distancias a dos puntos fijos de ese plano (Focos) es siempre igual a una constante (2a). Elementos de una hipérbola.- Entre los más importantes están: Centro “C”.- Punto medio entre los focos (F y F’) o entre los vértices (V y V’). Focos “F” y “F’ ”.- Puntos fijos de la hipérbola que se encuentran sobre el eje transverso. Vértices “V” y “V’ ”.- Extremos del eje transverso que indican la separación de la hipérbola. Vértices Secundarios “A” y “A’ ”.- Extremos del eje conjugado que indican el ancho de la hipérbola. Parámetro “a”.- Distancia entre el Centro y el Vértice. Parámetro “b”.- Distancia entre el Centro y el Vértice Secundario. Parámetro “c”.- Distancia entre el Centro y el Foco. Eje Transverso “2a”.- Distancia entre los vértices V y V’. Eje Conjugado “2b”.- Distancia entre los vértices secundarios A y A’. Lado Recto “LR”.- Segmento perpendicular al eje transverso que pasa por el foco e indica la abertura de la hipérbola. Excentricidad “e”.- Razón entre los parámetros “c” y “a”, indica la relación entre el largo y ancho de la hipérbola, siendo siempre mayor a 1. Hipérbola con centro en el origen.- Estas pueden ser: horizontales si la variable “x” aparece en la fórmula en primer lugar. verticales si la variable “y” aparece en la fórmula en primer lugar. Hipérbola horizontal con centro en el origen 𝑥2 − 𝑦2 =1 Ecuación: 𝑎2 Parámetros: 𝑐 2 = 𝑎2 + 𝑏 2 Excentricidad: 𝑒 Lado Recto: = 𝑏2 𝑐 𝑎 𝐿𝑅 = 2𝑏2 𝑎 Hipérbola vertical con centro en el origen Ecuación: Parámetros: 𝑦2 𝑥2 𝑎 𝑏2 =1 𝑐 2 = 𝑎2 + 𝑏 2 Excentricidad: 𝑒 Lado Recto: 2 − = 𝑐 𝑎 𝐿𝑅 = 2𝑏2 𝑎