Document
Anuncio
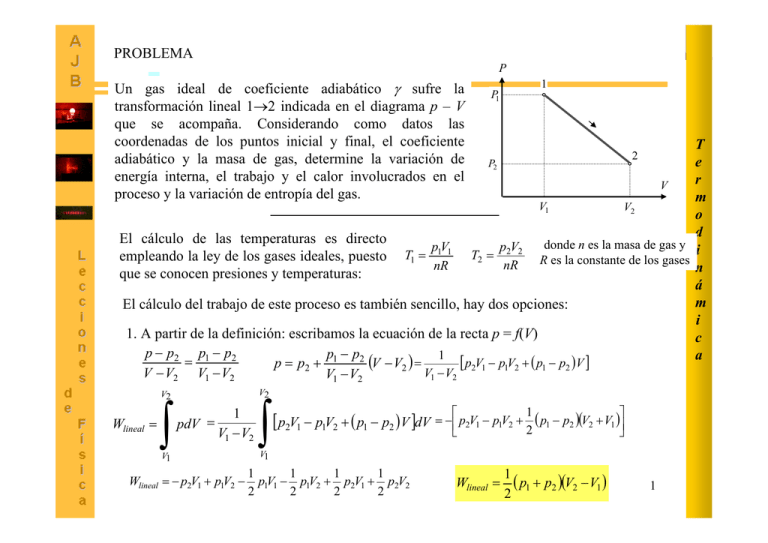
PROBLEMA P Un gas ideal de coeficiente adiabático γ sufre la transformación lineal 1→2 indicada en el diagrama p – V que se acompaña. Considerando como datos las coordenadas de los puntos inicial y final, el coeficiente adiabático y la masa de gas, determine la variación de energía interna, el trabajo y el calor involucrados en el proceso y la variación de entropía del gas. 1 P1 T e P2 r V m V1 V2 o d El cálculo de las temperaturas es directo donde n es la masa de gas y pV pV empleando la ley de los gases ideales, puesto T1 = 1 1 T2 = 2 2 R es la constante de los gases i nR nR n que se conocen presiones y temperaturas: á m El cálculo del trabajo de este proceso es también sencillo, hay dos opciones: i 1. A partir de la definición: escribamos la ecuación de la recta p = f(V) c p − p2 p1 − p2 p − p2 a = (V − V2 ) = 1 [ p2V1 − p1V2 + ( p1 − p2 )V ] p = p2 + 1 V1 − V2 V − V2 V1 − V2 V1 − V2 V2 V2 Wlineal = ∫ 2 pdV = 1 V1 − V2 V1 Wlineal = − p2V1 + p1V2 − ∫ [ p2V1 − p1V2 + ( p1 − p2 )V ]dV = −⎡⎢⎣ p2V1 − p1V2 + 2 ( p1 − p2 )(V2 + V1 )⎤⎥⎦ 1 V1 1 1 1 1 p1V1 − p1V2 + p2V1 + p2V2 2 2 2 2 Wlineal = 1 ( p1 + p2 )(V2 − V1 ) 2 1 P 2. Por consideraciones geométricas: Véase que la superficie comprendida bajo el segmento rectilíneo (que indica el proceso termodinámico) hasta el eje de abscisas (cuyo significado físico es el trabajo asociado al proceso) está dada por el área de un trapecio cuyo valor es: (El mismo resultado anterior) Wlineal W12 V V1 P3 P1 Consideremos el proceso lineal como parte del ciclo siguiente: En la adiabática 2 →3 se cumple p2V2 = p3V3 γ −1 T2 V2 3 Isoterma 1 Lineal γ −1 = T3 V3 Adiabática 1/(γ -1) Puesto que 3→1 es isotermo, T3 = T1 ⎛T ⎞ V3 = V2 ⎜⎜ 2 ⎟⎟ ⎝ T1 ⎠ Wlineal 1 = ( p1 + p2 )(V2 − V1 ) 2 V V3 V1 V2 ∆U ciclo = Qciclo − Wciclo = 0 Wisot = nRT1 ln Wadiab 2 P2 (aunque enseguida se verá que no es necesario conocer explícitamente V3) V V1 Qisot = Wisot = nRT1 ln 1 V3 V3 p V − p3V3 nR (T2 − T3 ) nR (T2 − T1 ) = 2 2 = = γ −1 γ −1 γ −1 V2 P Cálculo del calor asociado al proceso γ 2 P2 1 1 = (V2 − V1 ) p2 + (V2 − V1 )( p1 − p2 ) = ( p1 + p2 )(V2 − V1 ) 2 2 γ 1 P1 Qlineal + Qisot − Wlineal − Wisot − Wadiab = 0 Qlineal = Wlineal + Wadiab = nR (T − T ) 1 ( p1 + p2 )(V2 − V1 ) + γ 2− 1 1 2 Observación: Al calcular el trabajo del proceso adiabático, véase que Ti = T2, y que Tf = T3 = T1 2 T e r m o d i n á m i c a P Cálculo del calor asociado al proceso (procedimiento alternativo) 1 P1 T1 = p1V1 nR T2 = p2V2 nR (temperaturas calculadas antes) Vamos a considerar el proceso lineal 1→2 como parte del ciclo termodinámico que se indica al margen. T3 = p2V1 nR T 2 e P2 = P3 3 Si se obtienen los calores específicos a presión y volumen r Q V p constante a partir de los datos, es posible calcular el calor en m las etapas isobara e isocora. V1 = V3 V2 o γR R cP cP = d cV = cP − cV = R γ= ( ) γ − 1 ( ) γ − 1 cV i 1 Wlineal = (V2 − V1 )( p1 + p2 ) n γR (T3 − T2 ) = γ p2 (V1 − V2 ) < 0, cede energía Qisob = Q p = nc p (T3 − T2 ) = n 2 á γ −1 γ −1 Trabajo proceso 2 → 3 R m (T1 − T3 ) = 1 V1 ( p1 − p2 ) > 0, absorbe energía Qisocoro = QV = ncV (T1 − T3 ) = n i γ −1 γ −1 Wisob = W p = p2 (V1 − V2 ) c ∆U ciclo = Qciclo − Wciclo = 0 a Etapa 2→3: Isobara QV Etapa 3→1: Isocora El trabajo asociado al proceso 3 → 1 es nulo pues no hay variación de volumen Qlineal + Qisob + Qisocoro − Wlineal − Wisob = 0 Qlineal = − γ γ −1 p2 (V1 − V2 ) − 1 1 V1 ( p1 − p2 ) + (V2 − V1 )( p1 + p2 ) + p2 (V1 − V2 ) γ −1 2 ⎛ 1 ⎛ γ 1⎞ 1⎞ 1 1 + ⎟⎟ p1V1 + ⎜⎜ − ⎟⎟ p2V2 + p1V2 − p2V1 Qlineal = −⎜⎜ 2 2 ⎝ γ −1 2 ⎠ ⎝ γ −1 2 ⎠ Expresión equivalente a la obtenida anteriormente 3 P Cálculo de la variación de energía interna Una vez obtenido calor y trabajo, es inmediato aplicando el 1er principio ∆U12 = Qlineal − Wlineal P3 P1 3 Isoterma 1 Lineal Cálculo de variación de entropía de la transformación lineal ∆S ciclo = ∆S12 + ∆S 23 + ∆S31 = 0 ∆S12 = −∆S31 V = − nR ln 1 V3 La etapa 2→3 es adiabatica ⎡ V ⎛ T ⎞1 / (γ −1) ⎤ ⎥ ∆S12 = −nR ln ⎢ 1 ⎜⎜ 1 ⎟⎟ ⎢⎣V2 ⎝ T2 ⎠ ⎥⎦ Para un procedimiento alternativo para el cálculo de la entropía, vea la transparencia siguiente. T e Adiabática r 2 P2 V m o V2 V3 V1 d En la adiabática 2 →3 se cumple i p2V2γ = p3V3γ T2 V2γ −1 = T3 V3γ −1 n á Puesto que 3→1 es isotermo, T3 = T1 m i 1/(γ -1) ⎛T ⎞ c V3 = V2 ⎜⎜ 2 ⎟⎟ a ⎝ T1 ⎠ 1 / (γ −1) V1 V1 ⎛ T1 ⎞ = ⎜⎜ ⎟⎟ V3 V2 ⎝ T2 ⎠ 4 Cálculo de variación de entropía de la transformación lineal (procedimiento alternativo) Considerando el proceso lineal 1→2 como parte del ciclo termodinámico 1 P1 ∆S12 = −(∆S 23 + ∆S31 ) ∆S ciclo = ∆S12 + ∆S 23 + ∆S31 = 0 P b dS = δQ ∆S ab = T ∫ δQ T a 2 P2 = P3 Proceso isobaro 2→3 3 V V1 = V3 pV T1 = 1 1 nR pV T2 = 2 2 nR V2 pV T3 = 2 1 nR ⎛ V p ⎞ ∆S12 = − n⎜⎜ c p ln 1 + cV ln 1 ⎟⎟ V2 p2 ⎠ ⎝ T3 ∆S 23 = ∫ nc p dT T = nc p ln T3 V = nc p ln 1 T2 V2 T2 Proceso isocoro 3→1 T1 ∆S31 = ∫ T p ncV dT = ncV ln 1 = ncV ln 1 T3 p2 T T3 Este resultado es equivalente al obtenido en la transparencia anterior. 5 T e r m o d i n á m i c a