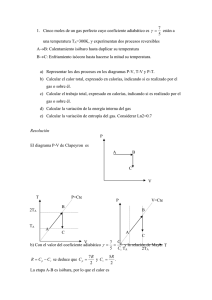
El ciclo reversible de Otto, está formado por dos procesos

El ciclo reversible de Otto, está formado por dos procesos adiabáticos y dos procesos
isócoros, en sentido horario.
Dos moles de un gas perfecto monoatómico (γ=5/3) realizan un ciclo de Otto, reduciéndose el
volumen a la tercera parte durante la compresión adiabática y triplicándose la presión durante
el calentamiento isócoro.
a) Calcular las temperaturas de los estados B, C y D, sabiendo que la temperatura del
estado inicial A es TA=400 K.
b) Calcular el rendimiento del ciclo y el rendimiento de un ciclo de Carnot que funcione
entre las mismas temperaturas extremas.
c) Calcular la variación de entropía en cada una de las etapas.
P Considerar 32/3 =2
B 3PA C PA A D V VA 3VA Resolución
1. a) En el proceso A-B se triplica la presión, manteniendo constante el volumen, por lo que
V = Cte =
nRTA nRTB
=
de donde la temperatura de B es triple de la de A
PA
3 PA
TB = 3T A = 3·400 K = 1200 K ; en el proceso adiabático B-C T BV Aγ −1 = TC ( 3V A )γ −1 , por tanto la
1
temperatura de C es TC = TB ⎛⎜ ⎞⎟
⎝3⎠
γ −1
TB
=
3
=
2/3
TB
, su valor es TC = 600 K
2
En el proceso adiabático D-A el volumen se reduce a la tercera parte, por tanto
γ −1
T AV A
= T D ( 3V A )
γ −1
,
⎛ 1⎞
TD = T A ⎜ ⎟
⎝3⎠
γ −1
=
TA
3
2/3
=
TA
2
, su valor es TD = 200 K
b) El trabajo realizado en el ciclo es suma de todos los calores, ya que la variación de energía
interna es nula; en las etapas B-C y D-A no se intercambia calor, por ser adiabáticas
W = Q AB + Q BC + QCD + Q DA = Q AB + QCD
El rendimiento es η =
Q
W
= 1 + CD
Q AB
Q AB
El calor intercambiado en los procesos isócoros A-B y C-D es
Q AB = ncV ( TB − T A )
QCD = ncV ( TD − TC )
QCD ncV ( TD − TC ) 200 − 600
=
=
= −0 ,5
Q AB ncV ( TB − T A ) 1200 − 400
η = 1 − 0 ,5 = 0 ,5
El rendimiento de un ciclo de Carnot que trabaje entre las mismas temperaturas extremas es
η=
1200 − 200 5
=
6
1200
c) La variación de entropía en las dos etapas adiabáticas (B-C y D-A) es nula
TB
En los procesos isócoros es S B − S A =
∫
TA
TD
S D − SC =
∫
TC
ncv dT
T
cal
cal
L3 = 6 L3
= nc v L B = 2 mol·3
TA
mol·K
K
T
ncv dT
T
cal
cal
L3 = −6 L3
= nc v L D = −2mol·3
TC
mol·K
K
T