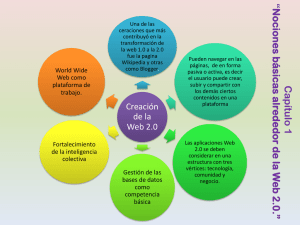
"número de copias vendidas a 18 €".
Anuncio

Abel Martín 026 "Programación Lineal" Una casa discográfica va a promocionar durante el próximo mes el último disco grabado por dos de los grupos más afamados bajo su sello. El precio de lanzamiento es 17.5 € y 18 €, respectivamente, siendo editadas 1500 copias del disco más caro. Para cubrir los gastos de la campaña debe vender en total 500 discos o más y por razones de imagen le conviene vender al menos tantas copias del disco más caro como del más barato. (a) ¿Cuántas copias de cada disco puede vender?. Plantea el problema y representa gráficamente su conjunto de soluciones. BH2 PAU OVIEDO junio 1997 (b) ¿Cuántas copias deberá vender de cada uno para maximizar sus ingresos ¿Cuál será su importe?. Resolución CON LÁPIZ Y PAPEL apartado (a) D S A T N G Ó C N E D N Ó C A N M R E T E D S AS TA NIIIT GN ÓG CÓ NC E IIIN DE ND ÓN CIIIÓ AC NA MIIIN RM ER TE ET DE x ≡ "número de copias vendidas a 17.5 €". y ≡ "número de copias vendidas a 18 €". C S E N O C C R T S E R E D O T N U J N O C S ES NE ON CIIIO CC RIIIC TR ST ES RE ER DE OD TO NT UN JU NJ ON CO y ≤ 1500 x ≤ y x + y ≥ 500 x ≥ 0 y ≥0 FFFU O V T E J B O N Ó C N U O VO TIIIV ET JE BJ OB NO ÓN CIIIÓ NC UN I(x, y): Ingresos expresados en € I(x, y) = 17.5x + 18y LLLA E B T C A N Ó G E R A E BLLLE TIIIB CT AC N FFFA ÓN GIIIÓ EG RE AR y ≥ 500 – x x≤y x y x y 0 500 0 0 500 0 200 200 D y ≤ 1500 C x ≤y A 200 B 200 x + y ≥ 500 El número de copias que puede vender de cada disco viene representado por los puntos (x, y) pertenecientes a la región factible, donde "x" es el número de copias vendidas a 17.50 € e "y" es el número de copias vendidas a 18 €, con la condición de que tanto "x" como "y" sean números naturales. Ejemplo: (200, 600) ∈ Región factible ¸ 200 copias de 17.5 € y 600 copias de 18 €. Otros puntos: (211, 1020), (200, 650), (410, 990), (600, 1020), (611, 995), etc. Resolución CON LÁPIZ Y PAPEL apartado (b) LLLO S E N O C U O S E D N Ó C A Z A C O S ES NE ON CIIIO UC OLLLU SO ES DE ND ÓN CIIIÓ AC ZA ALLLIIIZ CA OC Teorema: Como la región factible existe y está acotada, el valor óptimo de la función objetivo se alcanzará en uno de los vértices del polígono que limita la región, o a lo largo de uno de los lados. C S E C T R É V E D O U C Á C S::: ES CE TIIIC RT ÉR VÉ EV DE OD ULLLO CU ÁLLLC CÁ Los vértices A, C y D se observan a simple vista y con la ayuda de la tabla de valores: A (500, 0) C(1500, 1500) D (0, 1500) B(x, y) Resolvemos el sistema 14 Matemáticas y TIC Curso ON LINE Tema 6 x + y = 500 2x = 500 → x = 250 → y = 250 → B(250, 250) x= y A S O M T Ó E D S S Á N A S OS MO TIIIM ÓPPPT EÓ DE SD SIIIS ÁLLLIIIS NÁ AN Aplicamos el TEOREMA mencionado: Vértices Ingresos = 17.5·x + 18·y Valor A (500, 0) 17.5·500 + 18·0 8750 B (250, 250) 17.5·250 + 18·250 8875 C (1500, 1500) 17.5·1500 + 18·1500 53250 D (0, 1500) 17.5·0 + 18·1500 27000 A S O D A T U S E R S O E D O C T R C S S Á N A S OS DO AD TA ULLLT SU ES RE SR OS E LLLO DE OD CO TIIIC RÍÍÍT CR SC SIIIS ÁLLLIIIS NÁ AN El máximo beneficio se obtendrá cuando se vendan 1 500 copias del disco de 17.5 € y 1 500 copias de 18 €, momento en el que los ingresos ascenderán a 53250 €. 029 Los responsables de un videoclub han de realizar el pedido de películas de estreno y novedades a sus proveedores. El coste de cada película de estreno es de 7.6 € y el de cada novedad 3.7. Se desea un coste total que no supere los 945 €. Por otra parte, el proveedor les exige que los estrenos sean al menos la mitad que las novedades, y que las novedades más la mitad de los estrenos no sea inferior a las 100 unidades. (a) ¿De cuántas unidades de cada tipo puede consistir el pedido?. Plantear el problema y representar gráficamente el conjunto de soluciones. BH2 PAU OVIEDO Sept 1998 (b) Si se desea que el total de unidades pedidas sea mínimo, ¿de cuántas unidades de cada tipo ha de constar el pedido? ¿cuál es entonces el coste del pedido? Resolución CON LÁPIZ Y PAPEL apartado (a) D S A T N G Ó C N E D N Ó C A N M R E T E D S::: AS TA NIIIT GN ÓG CÓ NC E IIIN DE ND ÓN CIIIÓ AC NA MIIIN RM ER TE ET DE x ≡ "Número de películas de estreno". y ≡ "Número de películas de novedades". C S E N O C C R T S E R E D O T N U J N O C S ES NE ON CIIIO CC RIIIC TR ST ES RE ER DE OD TO NT UN JU NJ ON CO 7.6x + 3.7y ≤ 945 x ≥ y/2 y + x/2 ≥ 100 x≥0 7.6x + 3.7y ≤ 945 ¸ ¸ ¸ ¸ y≥0 2x – y ≥ 0 2y + x ≥ 200 x ≥ 0 y ≥ 0 LLLA E B T C A N Ó G E R A E BLLLE TIIIB CT AC N FFFA ÓN GIIIÓ EG RE AR 7.6x + 3.7y ≤ 945 x 0 124.3 y 255.4 0 2x – y ≥ 0 2y + x ≥ 200 x 0 5 x 0 200 y 0 10 C y 100 0 2x – y ≥ 0 x + 2y ≥ 200 A B 10 10 7.6x + 3.7y ≤ 945 El número de unidades de cada tipo de película que pueden constituir el pedido viene representado por los puntos (x, y) pertenecientes a la región factible, donde "x" es el número www.classpad.tk www.abelmartin.tk www.aulamatematica.tk 15 Abel Martín "Programación Lineal" de unidades de películas de estreno e "y" es el número de unidades de películas de novedades, con la condición de que tanto "x" como "y" sean números naturales: Ejemplo: (50, 80) ∈ Región factible Æ 50 películas de estreno y 80 películas de novedades. Otros puntos: (65, 82), (57, 97), (71, 94), (82, 67), etc. Resolución CON LÁPIZ Y PAPEL apartado (b) FFFU O V T E J B O N Ó C N U O VO TIIIV ET JE BJ OB NO ÓN CIIIÓ NC UN N(x, y): Número total de unidades pedidas N(x, y) = x + y LLLO S E N O C U O S E D N Ó C A Z A C O S ES NE ON CIIIO UC OLLLU SO ES DE ND ÓN CIIIÓ AC ZA ALLLIIIZ CA OC Teorema: Como la región factible existe y está acotada, el valor óptimo de la función objetivo se alcanzará en uno de los vértices del polígono que limita la región, o a lo largo de uno de los lados. Por lo tanto, lo primero que tendremos que hacer es averiguar los VÉRTICES del polígono que constituye la región factible: C S E C T R É V E D O U C Á C S ES CE TIIIC RT ÉR VÉ EV DE OD ULLLO CU ÁLLLC CÁ A(x, y) Resolvemos el sistema: (2) 2 x − y = 0 (1) x + 2 y = 200 4x − 2 y = 0 5x = 200 ¸ x = 40 ¸ y = 80 x + 2 y = 200 A(40, 80) B(x, y) Resolvemos el sistema: (10) 7.6 x + 3.7 y = 945 (−76) x + 2 y = 200 76 x + 37 y = 9450 – 115y = – 5750 − 76 x − 152 y = −15200 y = 50 ¸ x = 100 B(100, 50) C(x, y) Resolvemos el sistema: (10) 7.6 x + 3.7 y = 945 (37) 2x − y = 0 76 x + 37 y = 9450 150x = 9450 74 x − 37 y = 0 A S O M T Ó E D S S Á N A S OS MO TIIIM ÓPPPT EÓ DE SD SIIIS ÁLLLIIIS NÁ AN x = 63 Æ y = 126 C(63, 126) Aplicamos el TEOREMA mencionado: Vértices N(x, y) = x + y Valor A(40, 80) 40 + 80 120 B(100, 50) 100 + 50 150 C(63, 126) 63 + 126 189 Coste (x) = 7.60x + 3.70y Coste (x) = 7.60· 40 + 3.70 · 80 = 600 A S O D A T U S E R S O E D O C T R C S S Á N A S OS DO AD TA ULLLT SU ES RE SR OS E LLLO DE OD CO TIIIC RÍÍÍT CR SC SIIIS ÁLLLIIIS NÁ AN Para que el número de unidades sea mínimo el pedido ha de constar de 40 películas de estreno y 80 películas de novedades; En dicho momento el coste del pedido ascenderá a 600 €. 16 Matemáticas y TIC Curso ON LINE 030 Tema 6 Un grupo musical va a lanzar su nuevo trabajo al mercado. La casa discográfica considera necesario realizar una campaña intensiva de publicidad, combinando 2 posibilidades: anuncios en televisión, con un coste estimado de 1 millón de PTAS por anuncio, y cuñas radiofónicas, con un coste estimado de 100 000 PTAS por cuña. No obstante, no pueden gastar más de 100 millones de PTAS para dicha campaña, a lo largo de la cual se tienen que emitir al menos 50 y no más de 100 cuñas. Un estudio de mercado cifra en 10 000 el número de copias que se venderán por anuncio de televisión, y en 2 000 copias por cuña radiofónica emitida. a) ¿De cuántos anuncios y cuñas radiofónicas podrá constar esta campaña? Plantear el problema y representar gráficamente el conjunto de soluciones. b) ¿Qué combinación de ambos se debería realizar para vender el mayor número de copias posible? ¿se llegan a gastar los 100 millones de PTAS?. BH2 PAU OVIEDO JUNIO 1999 Resolución CON LÁPIZ Y PAPEL apartado (a) D S A T N G Ó C N E D N Ó C A N M R E T E D S AS TA NIIIT GN ÓG CÓ NC E IIIN DE ND ÓN CIIIÓ AC NA MIIIN RM ER TE ET DE x ≡ "número de anuncios en televisión". y ≡ "número de cuñas radiofónicas". C S E N O C C R T S E R E D O T N U J N O C S ES NE ON CIIIO CC RIIIC TR ST ES RE ER DE OD TO NT UN JU NJ ON CO 1 000 000x + 100 000y ≤ 100 000 000 y ≥ 50 y ≤ 100 ; x≥0 10x + y ≤ 1000 y ≥ 50 y ≤ 100 ; x ≥ 0 Æ Æ Æ LLLA E B T C A N Ó G E R A E BLLLE TIIIB CT AC N FFFA ÓN GIIIÓ EG RE AR 10x + y ≤ 1000 x y 0 1000 100 0 y ≤ 100 D A C B y ≥ 50 10 10x + y ≤ 1000 10 El número de anuncios y el número de cuñas viene representado por los puntos (x, y) pertenecientes a la región factible, donde "x" es el de anuncios en televisión e "y" es el número de cuñas radiofónicas, con la condición de que tanto "x" como "y" sean números naturales. Ejemplo: (52, 65) ∈ Región factible Æ 52 anuncios de televisión y 65 cuñas radiofónicas. Otros puntos: (37, 63), (15, 52), (5, 90), (55, 88), (88, 81), etc. Resolución CON LÁPIZ Y PAPEL apartado (b) FFFU O V T E J B O N Ó C N U O VO TIIIV ET JE BJ OB NO ÓN CIIIÓ NC UN C(x, y): Número total de copias que se venderán C(x, y) = 10 000x + 2000y LLLO S E N O C U O S E D N Ó C A Z A C O S ES NE ON CIIIO UC OLLLU SO ES DE ND ÓN CIIIÓ AC ZA ALLLIIIZ CA OC Teorema: Como la región factible existe y está acotada, el valor óptimo de la función objetivo se alcanzará en uno de los vértices del polígono que limita la región, o a lo largo de uno de los lados. Por lo tanto, lo primero que tendremos que hacer es averiguar los VÉRTICES del polígono que constituye la región factible: www.classpad.tk www.abelmartin.tk www.aulamatematica.tk 17 Abel Martín "Programación Lineal" C S E C T R É V E D O U C Á C S ES CE TIIIC RT ÉR VÉ EV DE OD ULLLO CU ÁLLLC CÁ Los vértices A y D se observan a simple vista y con la ayuda de la tabla de valores: A (0, 50) D (0, 100) B(x, 50) Resolvemos el sistema 10 x + y = 1000 y = 50 10x + 50 = 1000 → 10x = 950 → x = 95 B(95, 50) C(x, 100) Resolvemos el sistema 10 x + y = 1000 y = 100 10x + 100 = 1000 → 10x = 900 → x = 90 C(90, 100) A S O M T Ó E D S S Á N A S OS MO TIIIM ÓPPPT EÓ DE SD SIIIS ÁLLLIIIS NÁ AN Aplicamos el TEOREMA mencionado: Vértices A (0, 50) B (95, 50) C (90, 100) D (0, 100) Valor 100 000 1 050 000 1 100 000 200 000 C(x, y) = 10 000·x + 2000·y 10 000·0 + 2000·50 10 000·95 + 2000·50 10 000·90 + 2000·100 10 000·0 + 2000·100 Gasto = 90·1 000 000 + 100·100 000 = 100 000 000 PTAS A S O D A T U S E R S O E D O C T R C S S Á N A S OS DO AD TA ULLLT SU ES RE SR OS E LLLO DE OD CO TIIIC RÍÍÍT CR SC SIIIS ÁLLLIIIS NÁ AN Para vender el mayor número de copias posible se han de emitir en la campaña 90 anuncios en televisión y 100 cuñas radiofónicas, momento en el que se esperan vender 1 100 000 copias, gastándose en ese instante los 100 millones de PTAS. 032 Una fábrica de muebles produce dos líneas de muebles, "clásico" (C) y "funcional" (F). Para su fabricación, los muebles requieren tiempo de proceso de construcción y pintura. El mueble clásico precisa una unidad de tiempo de construcción y tres de pintura, mientras que el funcional requiere dos unidades de tiempo de construcción y una de pintura. La situación actual de la empresa no permite utilizar más de diez unidades de tiempo de construcción y quince de pintura. (a) Plantear el problema y representar gráficamente el conjunto de soluciones. BH2 PAU OVIEDO JUNIO 2000 (b) ¿Qué combinaciones de muebles puede fabricar?. (c) Si el beneficio empresarial es función del número de unidades fabricadas de acuerdo con la relación Bº= 3C + 2F, ¿cuántas unidades de cada línea deben fabricarse para maximizar el beneficio? ¿cuál es el beneficio máximo?. Resolución CON LÁPIZ Y PAPEL apartado (a) D S A T N G Ó C N E D N Ó C A N M R E T E D S AS TA NIIIT GN ÓG CÓ NC E IIIN DE ND ÓN CIIIÓ AC NA MIIIN RM ER TE ET DE x ≡ "Número de muebles de estilo clásico". y ≡ "Número de muebles de estilo funcional". Cuadro resumen Construcción (Unidades de tiempo) Pintura (Unidades de tiempo) Mueble clásico 1u 3u Mueble funcional 2u 1u C S E N O C C R T S E R E D O T N U J N O C S ES NE ON CIIIO CC RIIIC TR ST ES RE ER DE OD TO NT UN JU NJ ON CO 1x + 2y ≤ 10 Tiempo construcción 3x + 1y ≤ 15 Tiempo de pintura x≥0 y≥0 ¸ ¸ ¸ ¸ x + 2y ≤ 10 3x + y ≤ 15 x≥0 y≥0 LLLA E B T C A N Ó G E R A E BLLLE TIIIB CT AC N FFFA ÓN GIIIÓ EG RE AR x + 2y = 10 18 3x + y = 15 Matemáticas y TIC Curso ON LINE Tema 6 x 0 10 y 5 0 x 0 5 y 15 0 3x + y ≤ 15 x + 2y ≤ 10 B C 1 A D 1 Resolución CON LÁPIZ Y PAPEL apartado (b) El número de muebles de cada tipo que puede fabricar viene determinado por los puntos (x, y) pertenecientes a la región factible, donde "x" es el número de muebles de estilo clásico e "y" es el número de muebles de estilo funcional, con la condición de que tanto "x" como "y" sean números naturales. Así pues, las combinaciones de muebles que se pueden fabricar son las siguientes: 3x + y ≤ 15 x + 2y ≤ 10 B C 1 A D 1 Mueble clásico Mueble funcional Mueble clásico Mueble funcional Mueble clásico Mueble funcional 0 0 1 3 3 2 0 1 1 4 3 3 0 2 2 0 4 0 0 3 2 1 4 1 0 4 2 2 4 2 0 5 2 3 4 3 1 0 2 4 5 0 1 1 3 0 1 2 3 1 Resolución CON LÁPIZ Y PAPEL apartado (c) FFFU O V T E J B O N Ó C N U O VO TIIIV ET JE BJ OB NO ÓN CIIIÓ NC UN B(x, y): Beneficio expresado en unidades de beneficio B(x, y) = 3·x + 2·y LLLO S E N O C U O S E D N Ó C A Z A C O S ES NE ON CIIIO UC OLLLU SO ES DE ND ÓN CIIIÓ AC ZA ALLLIIIZ CA OC Teorema: Como la región factible existe y está acotada, el valor óptimo de la función objetivo se alcanzará en uno de los vértices del polígono que limita la región, o a lo largo de uno de los lados. Por lo tanto, lo primero que tendremos que hacer es averiguar los VÉRTICES del polígono que constituye la región factible: C S E C T R É V E D O U C Á C S ES CE TIIIC RT ÉR VÉ EV DE OD ULLLO CU ÁLLLC CÁ Los vértices A, B y D se observan a simple vista y con la ayuda de la tabla de valores: A (0, 0) B(0, 5) D(5, 0) C(x, y) Resolvemos el sistema: www.classpad.tk www.abelmartin.tk www.aulamatematica.tk 19 Abel Martín "Programación Lineal" (−3) x + 2 y = 10 (1) 3 x + y = 15 − 3x − 6 y = −30 – 5y = – 15 3x + y = 15 3x + 3 = 15 Æ y = 3 Æ 3x = 12 Æ x = 4 C(4, 3) A S O M T Ó E D S S Á N A S OS MO TIIIM ÓPPPT EÓ DE SD SIIIS ÁLLLIIIS NÁ AN Aplicamos el TEOREMA mencionado: Vértices B(x, y) = 3·x + 2·y Valor A (0, 0) 3·0 + 2·0 0 B (0, 5) 3·0 + 2·5 10 C (4, 3) 3·4 + 2·3 18 D (5, 0) 3·5 + 2·0 15 A S O D A T U S E R S O E D O C T R C S S Á N A S OS DO AD TA ULLLT SU ES RE SR OS E LLLO DE OD CO TIIIC RÍÍÍT CR SC SIIIS ÁLLLIIIS NÁ AN Para obtener el máximo beneficio empresarial han de fabricarse 4 muebles de estilo clásico y 3 muebles de estilo funcional, momento en el que éste ascenderá a 18 unidades de beneficio. ANÁLISIS GRÁFICO DE ÓPTIMOS CON LA AYUDA DE UNA CALCULADORA GRÁFICA Observemos la recta que representa a la función objetivo cuyos beneficios son nulos: 3 x + 2 y = 0 −3 En forma explícita ¸ y = x ¸ m = – 3/2 2 De todas las infinitas rectas paralelas a ésta de beneficios nulos que pasan por el conjunto de restricciones, la que corresponde a unos beneficios máximos será aquella que corte al eje OY por el punto más alejado del origen. Estas líneas de nivel serán rectas que tienen por ecuación la forma y – y1 = m ( x – x1 ) Ésta es la ecuación de la recta de pendiente "m" que pasa por el punto (x1, y1). En forma explícita, para representarla en la calculadora, vendrá determinada por: y = m ( x – x1 ) + y1 (4, 3) 040 Una compañía minera tiene dos explotaciones: Una explotación A obtiene diariamente 200 Kg de Cinc, 100 Kg de Cobre y 400 Kg de Plomo. La explotación B obtiene diariamente 100 Kg de Cinc, 200 Kg de Cobre y 400 Kg de Plomo. La compañía necesita en los próximos años, al menos 40 Toneladas de Cinc, 50 Toneladas de Cobre y 140 Toneladas de Plomo. Sabiendo que el coste diario por Kg es de 60 € en la mina A y 45 € en la mina B ¿Cuántos Kg se deben de extraer de cada mina para que el coste sea mínimo? Resolución CON LÁPIZ Y PAPEL apartado (a) D S A T N G Ó C N E D N Ó C A N M R E T E D S::: AS TA NIIIT GN ÓG CÓ NC E IIIN DE ND ÓN CIIIÓ AC NA MIIIN RM ER TE ET DE x ≡ "Número de días de trabajo en la mina A. y ≡ "Número de días de trabajo en la mina B. C S E N O C C R T S E R E D O T N U J N O C S ES NE ON CIIIO CC RIIIC TR ST ES RE ER DE OD TO NT UN JU NJ ON CO 200 x +100 y ≥ 40 000 Kg Cinc 20 → Matemáticas y TIC y ≥ 400 – 2x BH2 Curso ON LINE Tema 6 100 x + 200 y ≥ 50 000 Kg Cobre 400 x + 400 y ≥ 140 000 Kg Plomo x≥0 y≥0 → y ≥ 250 – 0.5x → y ≥ 350 – x → x≥0 y ≥0 LLLA E B T C A N Ó G E R A E BLLLE TIIIB CT AC N FFFA ÓN GIIIÓ EG RE AR 2x + y = 400 x + 2y = 500 x + y = 350 x 0 200 x 0 500 x 0 350 y 400 0 y 250 0 y 350 0 D C x + 2y = 500 B A 2x + y = 400 x + y = 350 FFFU O V T E J B O N Ó C N U O VO TIIIV ET JE BJ OB NO ÓN CIIIÓ NC UN C C C(((xxx,,, yyy))) === 666000 xxx +++ 444555 yyy LLLO S E N O C U O S E D N Ó C A Z A C O S... ES NE ON CIIIO UC OLLLU SO ES DE ND ÓN CIIIÓ AC ZA ALLLIIIZ CA OC Teorema: Como la región factible no es acotada, la función objetivo no alcanza necesariamente un valor óptimo concreto, pero si lo hace, éste se encuentra en uno de los vértices de la región. Por lo tanto, lo primero que tendremos que hacer es averiguar los VÉRTICES del polígono que constituye la región factible: C S E C T R É V E D O U C Á C S::: ES CE TIIIC RT ÉR VÉ EV DE OD ULLLO CU ÁLLLC CÁ Los vértices A y C se observan a simple vista y con la ayuda de la tabla de valores: A(0, 400) C(x, y) D(500, 0) Resolvemos el sistema (−1) x + y = 350 2 x + y = 400 − x − y = −350 x = 50 → y = 350 – x 2 x + y = 400 y = 350 - 50 → y = 300 B(x, y) C(50, 300) Resolvemos el sistema (−1) x + 2 y = 500 (1) x + y = 350 − x − 2 y = −500 – y = - 150 → y = 150 x + y = 350 x = 350 - y → x = 350 - 150 → x = 200 B(200, 150) A S O M T Ó E D S S Á N A S OS MO TIIIM ÓPPPT EÓ DE SD SIIIS ÁLLLIIIS NÁ AN Aplicamos el TEOREMA mencionado: Vértices B(x, y) = 60·x + 45·y Valor A (0, 400) 60·0 + 45·400 = 18 000 B (200, 150) 60·200 + 45·150 = 18 750 C (50, 300) 60·50 + 45·300 = 16 500 D (500, 0) 60·500 + 45·0 = 30 000 Tanteamos a ojo y vemos que no hay otros valores de la región factible que la hagan menor que el del punto a (50, 300). Á N A S O D A T U S E R S O E D O C T R C S S N A S OS DO AD TA ULLLT SU ES RE SR OS E LLLO DE OD CO TIIIC RÍÍÍT CR SC SIIIS ÁLLLIIIS ANÁ www.classpad.tk www.abelmartin.tk www.aulamatematica.tk 21 Abel Martín "Programación Lineal" En la mina A se debe de trabajar 50 días y en la mina B 300 días para que el coste sea mínimo, momento en el que dicho coste asciende a 16 500 €. ANÁLISIS GRÁFICO DE ÓPTIMOS CON LA AYUDA DE UNA CALCULADORA GRÁFICA Veamos la recta que representa los costes son nulos:: C(x, y) = 60 x + 45 y 60 x + 45 y = 0 ¸ En forma explícita ¸ y = − 6000 4500 x ¸ y = (– 4/3)x De todas las infinitas rectas paralelas a ésta de costes nulos que pasan por el conjunto de restricciones, la que corresponde a un mínimo será aquella que corte al eje OY por el punto más cercano al origen. Veamos cuál es ésta, trazando mentalmente paralelas a la recta y = (- 4/3)x y que pasen por los vértices: → → → → ¡Confirmado!: en la mina A se debe de trabajar 50 días y en la mina B 300 días para que el coste sea mínimo, momento en el que dicho coste asciende a 16 500 €. 041 Una persona decide invertir parte o todo su dinero, 50 000 €, en un banco, atendiendo a la siguiente oferta: Una cantidad, que será inferior a 30 000 €, tendrá un rendimiento del 7% y otra cantidad un rendimiento de 9%, debiendo de invertir, como máximo, 10 000 € más en la de rendimiento de 7%. (a) ¿Cuánto debe invertir en cada modalidad para que el beneficio obtenido sea el máximo?. (b) ¿A cuánto asciende dicho beneficio?. Resolución CON LÁPIZ Y PAPEL apartado (a) D S A T N G Ó C N E D N Ó C A N M R E T E D S::: AS TA NIIIT GN ÓG CÓ NC E IIIN DE ND ÓN CIIIÓ AC NA MIIIN RM ER TE ET DE x ≡ "€ ( expresados en 10 millares) que debe de invertir al 7%. y ≡ "€ ( expresados en 10 millares) que debe de invertir al 9%. C S E N O C C R T S E R E D O T N U J N O C S ES NE ON CIIIO CC RIIIC TR ST ES RE ER DE OD TO NT UN JU NJ ON CO x≤3 x+y≤5 x ≤ y + 1 (x – 1 ≤ y) x≥0 y≥0 LLLA E B T C A N Ó G E R A E BLLLE TIIIB CT AC N FFFA ÓN GIIIÓ EG RE AR x+y=5 x 0 5 22 y 5 0 x-y=1 x 0 1 Matemáticas y TIC y –1 0 BH2 Curso ON LINE Tema 6 D x= y+1 C 1 B A 1 x+ y=5 FFFU O V T E J B O N Ó C N U O VO TIIIV ET JE BJ OB NO ÓN CIIIÓ NC UN R R R(((xxx,,, yyy))) === 000...000777xxx +++ 000...000999yyy LLLO S E N O C U O S E D N Ó C A Z A C O S... ES NE ON CIIIO UC OLLLU SO ES DE ND ÓN CIIIÓ AC ZA ALLLIIIZ CA OC Teorema: Como la región factible existe y está acotada, el valor óptimo de la función objetivo se alcanzará en uno de los vértices del polígono que limita la región, o a lo largo de uno de los lados. Por lo tanto, lo primero que tendremos que hacer es averiguar los VÉRTICES del polígono que constituye la región factible: C S E C T R É V E D O U C Á C S::: ES CE TIIIC RT ÉR VÉ EV DE OD ULLLO CU ÁLLLC CÁ Los vértices A y C se observan a simple vista y con la ayuda de la tabla de valores: A(0, 0) C(x, y) x+ y =5 B(1, 0) D(0, 5) Resolvemos el sistema x = y + 1 y + 1 + y = 5 → 2y = 4 → y = 2 x=y+1=2+1 → x=3 C(3, 2) A S O M T Ó E D S S Á N A S OS MO TIIIM ÓPPPT EÓ DE SD SIIIS ÁLLLIIIS NÁ AN Aplicamos el TEOREMA mencionado: Vértices R(x, y) = 0.07x + 0.09y Valor A (0, 0) 0.07·0 + 0.09·0 = 0 B (1, 0) 0.07·1 + 0.09·0 = 0.07 C (3, 2) 0.07·3 + 0.09·2 = 0.39 D (0, 5) 0.07·0 + 0.09·5 = 0.45 NOTA: Recuerda que las unidades venían expresadas en 10 millares: 0.45·10000 = 4 500 A S O D A T U S E R S O E D O C T R C S S Á N A S OS DO AD TA ULLLT SU ES RE SR OS E LLLO DE OD CO TIIIC RÍÍÍT CR SC SIIIS ÁLLLIIIS NÁ AN El máximo rendimiento se obtendrá cuando se coloquen 0 € al 7% y 50 000 € al 9% momento en el que se obtiene un rendimiento de 4500 €. ANÁLISIS GRÁFICO DE ÓPTIMOS CON LA AYUDA DE UNA CALCULADORA GRÁFICA Veamos la recta que representa a la función objetivo cuyo rendimiento es nulo: R(x, y) = 0.07x + 0.09y = 0 En forma explícita ¸ y = − 0.07 x 0.09 ¸ y = (– 7/9)x EN LA PRÁCTICA representamos esta recta y buscamos MENTALMENTE , de todas las infinitas rectas paralelas a ésta (m = – 7/9), la que corresponde a unos rendimientos máximos, es decir, la que corta al eje OY por el punto más lejano al origen. www.classpad.tk www.abelmartin.tk www.aulamatematica.tk 23 Abel Martín "Programación Lineal" → → → → ¡Confirmado!: El máximo rendimiento se obtendrá cuando se coloquen 0 € al 7% y 50 000 € al 9% momento en el que se obtiene un rendimiento de 4500 €. 047 Un inversor dispone de 20000 € que quiere invertir en dos tipos de bonos. La rentabilidad de los bonos A es del 17% y la de los bonos B tienen una rentabilidad del 9%. Si por cada € invertido en bonos A es preciso invertir al menos dos en bonos B. BH2 a) ¿Cuánto dinero se debe colocar en cada tipo de bonos para que el rendimiento sea máximo?. b) ¿A cuanto ascenderá dicha rentabilidad?. Resolución CON LÁPIZ Y PAPEL apartado (a) D S A T N G Ó C N E D N Ó C A N M R E T E D S::: AS TA NIIIT GN ÓG CÓ NC E IIIN DE ND ÓN CIIIÓ AC NA MIIIN RM ER TE ET DE x ≡ "Miles de € invertidos en bonos del tipo A". y ≡ "Miles de € invertido en bonos del tipo B". C S E N O C C R T S E R E D O T N U J N O C S ES NE ON CIIIO CC RIIIC TR ST ES RE ER DE OD TO NT UN JU NJ ON CO x + y ≤ 20 2x ≤ y x≥0 y≥0 LLLA E B T C A N Ó G E R A E BLLLE TIIIB CT AC N FFFA ÓN GIIIÓ EG RE AR x + y = 20 x 0 20 y = 2x y 20 0 x 0 20 y 0 40 2x ≤ y C B 5 A 5 x + y ≤ 20 FFFU O V T E J B O N Ó C N U O VO TIIIV ET JE BJ OB NO ÓN CIIIÓ NC UN B(x, y) = 0.17x + 0.09y LLLO S E N O C U O S E D N Ó C A Z A C O S... ES NE ON CIIIO UC OLLLU SO ES DE ND ÓN CIIIÓ AC ZA ALLLIIIZ CA OC Teorema: Como la región factible existe y está acotada, el valor óptimo de la función objetivo se alcanzará en uno de los vértices del polígono que limita la región, o a lo largo de uno de los lados. Por lo tanto, lo primero que tendremos que hacer es averiguar los VÉRTICES del polígono que constituye la región factible: C S E C T R É V E D O U C Á C S::: ES CE TIIIC RT ÉR VÉ EV DE OD ULLLO CU ÁLLLC CÁ Los vértices A y C se observan a simple vista y con la ayuda de la tabla de valores: A(0, 0) 24 C(0, 20) Matemáticas y TIC Curso ON LINE B(x, y) Tema 6 Resolvemos el sistema 2x − y = 0 3x = 20 → x = 20/3 → y = 40/3 x + y = 20 B(20/3, 40/3) A S O M T Ó E D S S Á N A S OS MO TIIIM ÓPPPT EÓ DE SD SIIIS ÁLLLIIIS NÁ AN Aplicamos el TEOREMA mencionado: Vértices A (0,0) B (6.6, 13.3) C (0, 20) Beneficio = 0.17·x + 0.09·y 0.17 · 0 + 0.09 · 0 0.17 · 6.6 + 0.09 · 13.3 0.17 · 0 + 0.09 · 20 Valor 0 2.333333 1.8 A S O D A T U S E R S O E D O C T R C S S Á N A S OS DO AD TA ULLLT SU ES RE SR OS E LLLO DE OD CO TIIIC RÍÍÍT CR SC SIIIS ÁLLLIIIS NÁ AN El máximo beneficio se obtendrá cuando se inviertan 6 666.67 € en bonos de tipo A y 13 333.33 € en bonos de tipo B, momento en el que la rentabilidad será de 2 333.33 €. 049 En la elaboración de un determinado producto farmacológico se utilizan dos tipos de pastillas de 40 gr. y 30 gr. Cada frasco ha de contener como máximo 600 gramos, necesitándose, por razones de stock, al menos tres pastillas grandes y al menos el doble de pequeñas que de grandes. BH2 Cada pastilla grande proporciona un beneficio de 2 € y la pequeña de 1 €. ¿Cuántas pastillas se han de elaborar de cada clase para que el beneficio sea máximo? Resolución CON LÁPIZ Y PAPEL D S A T N G Ó C N E D N Ó C A N M R E T E D S AS TA NIIIT GN ÓG CÓ NC E IIIN DE ND ÓN CIIIÓ AC NA MIIIN RM ER TE ET DE x ≡ "número de pastillas grandes". y ≡ "número de pastillas pequeñas". C S E N O C C R T S E R E D O T N U J N O C S ES NE ON CIIIO CC RIIIC TR ST ES RE ER DE OD TO NT UN JU NJ ON CO → → → → 40x + 30y ≤ 600 y ≥ 2x x≥3 y≥0 4x + 3y ≤ 60 y ≥ 2x x≥3 y≥0 LLLA E B T C A N Ó G E R A E BLLLE TIIIB CT AC N FFFA ÓN GIIIÓ EG RE AR 4x + 3y = 60 x y 0 20 15 0 y = 2x x 0 10 y 0 20 y ≥ 2x C B 5 A 4x + 3y ≤ 60 5 FFFU O V T E J B O N Ó C N U O VO TIIIV ET JE BJ OB NO ÓN CIIIÓ NC UN B(x, y): Beneficio expresado en € B(x, y) = 2x + y LLLO S E N O C U O S E D N Ó C A Z A C O S ES NE ON CIIIO UC OLLLU SO ES DE ND ÓN CIIIÓ AC ZA ALLLIIIZ CA OC www.classpad.tk www.abelmartin.tk www.aulamatematica.tk 25 Abel Martín "Programación Lineal" Teorema: Como la región factible existe y está acotada, el valor óptimo de la función objetivo se alcanzará en uno de los vértices del polígono que limita la región, o a lo largo de uno de los lados. Por lo tanto, lo primero que tendremos que hacer es averiguar los VÉRTICES del polígono que constituye la región factible: C S E C T R É V E D O U C Á C S::: ES CE TIIIC RT ÉR VÉ EV DE OD ULLLO CU ÁLLLC CÁ A(3, y) Resolvemos el sistema por sustitución: y = 2x → y = 2·3 → y = 6 A (3, 6) B(x , y) Resolvemos el sistema por sustitución: 4 x + 3 y = 60 4x + 3·2x = 60 → 4x + 6x = 60 → 10x = 60 → x = 6 y = 2 x B (6, 12) C(3, y) Resolvemos el sistema por sustitución: 4x + 3y = 60 → 4·3 + 3y = 60 → 3y = 60 - 12 → y = 16 C (3, 16) A S O M T Ó E D S S Á N A S OS MO TIIIM ÓPPPT EÓ DE SD SIIIS ÁLLLIIIS NÁ AN Aplicamos el TEOREMA mencionado: Vértices B(x, y) = 2 x + 1 y Valor A (3, 6) 23+16 12 B(6, 12) 2 6 + 1 12 24 C(3, 16) 2 3 + 1 16 22 A S O D A T U S E R S O E D O C T R C S S Á N A S OS DO AD TA ULLLT SU ES RE SR OS E LLLO DE OD CO TIIIC RÍÍÍT CR SC SIIIS ÁLLLIIIS NÁ AN Para que el beneficio sea máximo se tendrán que elaborar 6 pastillas de 40 gramos y 12 pastillas de 30 gramos, momento en el que el beneficio ascenderá a 24 €. 056 Se dispone de 600 gramos de un determinado fármaco para elaborar pastillas grandes y pequeñas. Las grandes pesan 40 gramos y las pequeñas 30 gramos. Se necesitan como mínimo 5 pastillas pequeñas y al menos el doble de las pequeñas que de las grandes. Cada pastilla grande proporciona un beneficio de 50 céntimos de euro y las pequeñas de 30 céntimos de euro. (a) Plantea el problema, representa e indica el conjunto solución para saber el número de pastillas de cada clase que se pueden elaborar. (b) Calcula el número de pastillas de cada clase para que el beneficio sea máximo. ¿A cuánto asciende dicho beneficio? Resolución CON LÁPIZ Y PAPEL apartado (a) D S A T N G Ó C N E D N Ó C A N M R E T E D S AS TA NIIIT GN ÓG CÓ NC E IIIN DE ND ÓN CIIIÓ AC NA MIIIN RM ER TE ET DE x ≡ "número de pastillas grandes". y ≡ "número de pastillas pequeñas". C S E N O C C R T S E R E D O T N U J N O C S ES NE ON CIIIO CC RIIIC TR ST ES RE ER DE OD TO NT UN JU NJ ON CO 40x + 30y ≤ 600 y≥5 y ≥ 2x x≥0 → → → → 4x + 3y ≤ 60 y≥5 y ≥ 2x LLLA E B T C A N Ó G E R A E BLLLE TIIIB CT AC N FFFA ÓN GIIIÓ EG RE AR 4x + 3y = 60 x y 0 20 26 y = 2x x 0 Matemáticas y TIC y 0 x≥0 BH2 Curso ON LINE Tema 6 15 0 10 20 y ≥ 2x D C 10 y≥5 A B 5 4x + 3y ≤ 60 FFFU O V T E J B O N Ó C N U O VO TIIIV ET JE BJ OB NO ÓN CIIIÓ NC UN B(x, y): Beneficio expresado en céntimos de € B(x, y) = 50x + 30y LLLO S E N O C U O S E D N Ó C A Z A C O S ES NE ON CIIIO UC OLLLU SO ES DE ND ÓN CIIIÓ AC ZA ALLLIIIZ CA OC Teorema: Como la región factible existe y está acotada, el valor óptimo de la función objetivo se alcanzará en uno de los vértices del polígono que limita la región, o a lo largo de uno de los lados. Por lo tanto, lo primero que tendremos que hacer es averiguar los VÉRTICES del polígono que constituye la región factible: C S E C T R É V E D O U C Á C S::: ES CE TIIIC RT ÉR VÉ EV DE OD ULLLO CU ÁLLLC CÁ Los vértices A y D se observan a simple vista y con la ayuda de la tabla de valores: A(0, 5) B(x , 5) D(0, 15) Resolvemos el sistema por sustitución: y = 2x → 5 = 2x → x = 2.5 C(x , y) Æ B(2.5, 5) Resolvemos el sistema por sustitución: 4 x + 3 y = 60 4x + 3·2x = 60 → 4x + 6x = 60 → 10x = 60 → x = 6 y = 2 x Æ C(6, 12) A S O M T Ó E D S S Á N A S OS MO TIIIM ÓPPPT EÓ DE SD SIIIS ÁLLLIIIS NÁ AN Aplicamos el TEOREMA mencionado: Vértices B B = 5 0 · + 3 0 · B(((xxx,,, yyy))) = =5 50 0· ·xxx + +3 30 0· ·yyy Valor A(0, 5) 50·0 + 30·5 150 ctos B(2.5, 5) 50·2.5 + 30·5 275 ctos C(6, 12) 50·6 + 30·12 660 ctos D(0, 15) 50·0 + 30·15 450 ctos A S O D A T U S E R S O E D O C T R C S S Á N A S OS DO AD TA ULLLT SU ES RE SR OS E LLLO DE OD CO TIIIC RÍÍÍT CR SC SIIIS ÁLLLIIIS NÁ AN Para que el beneficio sea máximo se tendrán que elaborar 6 pastillas de 40 gramos y 12 pastillas de 30 gramos, momento en el que el beneficio ascenderá a 6.6 €. www.classpad.tk www.abelmartin.tk www.aulamatematica.tk 27