Ejercicio nº 1.- Al preguntar a 30 parejas jóvenes sobre el número

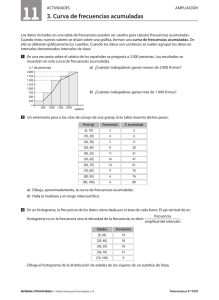
Ejercicio nº 1.-
Al preguntar a 30 parejas jóvenes sobre el número de hijos que desearían tener, hemos
obtenido estas respuestas:
a) Elabora una tabla de frecuencias absolutas, relativas, acumuladas y porcentajes.
b) Representa gráficamente la distribución.
c) ¿Qué significa el 7 de la columna de frecuencias absolutas?
d) ¿Qué significa el 23 que se encuentra en la columna de frecuencias acumuladas?
e) ¿Qué porcentaje de parejas quiere tener 3 hijos o más?
Solución:
a)
b)
c) Significa que 7 parejas desean tener un hijo.
d) Significa que 12 parejas desean tener 2 hijos o menos.
e) 13 % + 7 % + 3 % = 23 %
El 23 % de las parejas encuestadas quieren tener 3 hijos o más.
Ejercicio nº 2.-
Se pregunta a un grupo de estudiantes por el número de libros que han leído en el último mes,
obteniendo las siguientes respuestas:
N.° DE LIBROS
0
1
2
3
4
5
N.° DE
ESTUDIANTES
1
15
38
16
7
3
a) Halla la media y la desviación típica.
b) ¿Qué porcentaje de estudiantes leen un número de libros superior a la media?
c) En otro grupo de estudiantes, realizado el mismo estudio, hemos obtenido una media de 3,5
y una desviación típica de 2,8. Calcula el coeficiente de variación en los dos casos y compara
la dispersión en ambos grupos.
Solución:
a)
Media:
Desviación típica:
b) Por encima de la media hay 16 7 3 = 26 estudiantes de 80 que hay en total. Por tanto:
El 32,5 % de los estudiantes lee un número de libros superior a la media.
Es bastante mayor la dispersión en el segundo grupo.
Ejercicio nº 3.-
La siguiente tabla indica el número de faltas de asistencia a clase de Educación Física de
cierto grupo de estudiantes de 3.º ESO durante el mes pasado:
N.º de faltas
Frecuencia
0
7
1
1
2
3
3
2
4
5
5
7
6
5
a) Construye la tabla de frecuencias acumuladas y utilizándola halla la mediana y los cuartiles.
b) Representa los datos obtenidos en un diagrama de caja y bigotes.
Solución:
a)
N.º de faltas
frecuencia
frecuencias acumuladas
0
7
7
1
1
8
2
3
11
3
2
13
4
5
18
5
7
25
6
5
30
El total de datos es 30, 30 : 2 = 15, la mediana está entre los lugares 15.º y 16.º, mirando en la
columna de las frecuencias acumuladas de los estudiantes 14.º al 18.º tuvieron 4 faltas, por tanto Me
= 4.
30 : 4 = 7,5, el primer cuartil está en el 8.º lugar, mirando en la columna de frecuencias acumuladas
el estudiante que ocupa el 8.º lugar tuvo una falta, Q1= 1.
7,5 = 3 = 22,5, el tercer cuartil está en el lugar 23.º, mirando la columna de frecuencias acumuladas,
los estudiantes que ocupan los lugares del 19.º al 25.º tuvieron 5 faltas, por tanto Q3= 5.
b)
Ejercicio nº 4.-
La siguiente gráfica muestra el peso de 40 alumnos de 3.° ESO.
Interpreta la gráfica y haz una tabla de frecuencias a partir de ella. ¿Cuál es el peso medio?
Solución:
La mayor parte de los alumnos tiene un peso entre 52,5 kg y 73,5 kg. Por tanto, aquellos alumnos
cuyo peso esté fuera de ese intervalo se considerará que tienen falta de peso o sobrepeso.
Hacemos la tabla de frecuencias asignada a este histograma:
Intervalo
xi
fi
fixi
45,5 - 52,5
49
2
98
52,5 - 59,5
56
11
616
59,5 - 66,5
63
12
756
66,5 - 73,5
70
10
700
73,5 - 80,5
77
4
308
80,5 - 87,5
84
1
84
40
2 562
64 kg.
Ejercicio nº 5.-
a) Una urna contiene 12 bolas amarillas, 15 verdes y 23 azules. Calcula la probabilidad de que
al extraer una bola al azar sea de color amarillo.
b) Lanzamos dos dados y observamos sus puntuaciones.
b1) Describe el espacio muestral.
b2) ¿Cuál es la probabilidad de obtener dos números iguales?
b3) ¿Cuál es la probabilidad de obtener al menos un número impar?
b4) ¿Cuál es la probabilidad de obtener dos múltiplos de 3?
Solución:
Ejercicio nº 6.-
En una caja tenemos 10 bolas numeradas del 0 al 9. Al extraer una bola 50 veces hemos
obtenido los resultados de la tabla:
BOLA
FREC.
0
5
1
5
2
4
3
6
4
3
5
6
6
5
7
6
8
5
9
5
a) Construye la tabla de frecuencias absoluta y relativa de cada suceso.
b) Estima la probabilidad del suceso "obtener puntuación impar".
Solución:
a)
FA
FRELATIVA
0
5
5/50 = 0,10
1
5
5/50 = 0,10
2
4
4/50 = 0,08
3
6
6/50 = 0,12
4
3
3/50 = 0,06
5
6
6/50 = 0,12
6
5
5/50 = 0,10
7
6
6/50 = 0,12
8
5
5/50 = 0,10
9
5
5/50 = 0,10
b) fr[IMPAR] = 28/50 = 0,56 → P
0,56
Ejercicio nº 7.-
Tengo en una caja las dieciséis fichas del parchís y saco al azar dos fichas, sin
reemplazamiento. Mediante un diagrama de árbol, calcula la probabilidad de que:
a) Las dos fichas sean amarillas.
b) Una ficha sea verde y la otra roja.
c) Las dos fichas sean del mismo color.
Solución:
Ejercicio nº 8.-
Saco, sin devolución, tres cartas de una baraja española. Calcula la probabilidad de que:
a) Las tres sean ases.
b) Una sea figura y las otras ases.
c) Dos sean figuras.
Solución: