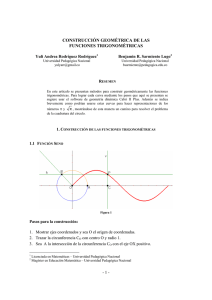
PVP PHP P` P P` P P b a` b` d c` d` o a c
Anuncio
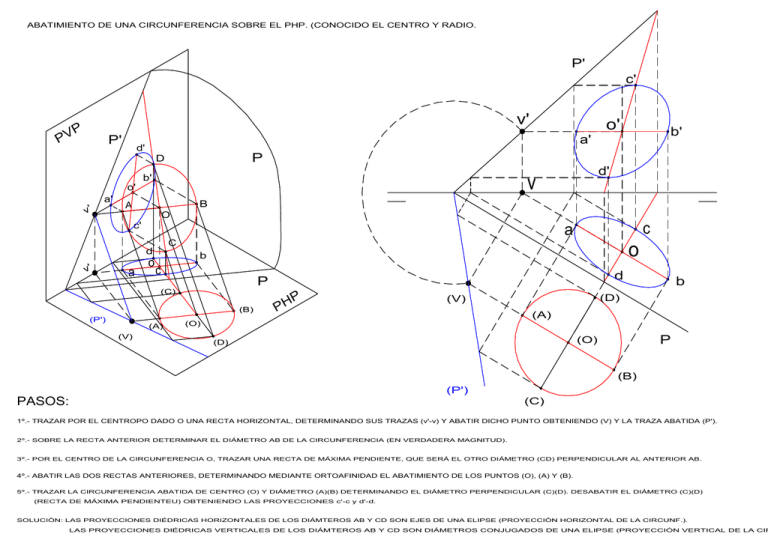
ABATIMIENTO DE UNA CIRCUNFERENCIA SOBRE EL PHP. (CONOCIDO EL CENTRO Y RADIO. P' P v' VP P' v' a' a' d' o' A O a o a c (A) c d P (B) (V) o b (C) (P') b' B C d o' d' v b' c' v' P D c' P PH b (D) (V) (A) (O) P (O) (D) (B) (P') PASOS: (C) 1º.- TRAZAR POR EL CENTROPO DADO O UNA RECTA HORIZONTAL, DETERMINANDO SUS TRAZAS (v'-v) Y ABATIR DICHO PUNTO OBTENIENDO (V) Y LA TRAZA ABATIDA (P'). 2º.- SOBRE LA RECTA ANTERIOR DETERMINAR EL DIÁMETRO AB DE LA CIRCUNFERENCIA (EN VERDADERA MAGNITUD). 3º.- POR EL CENTRO DE LA CIRCUNFERENCIA O, TRAZAR UNA RECTA DE MÁXIMA PENDIENTE, QUE SERÁ EL OTRO DIÁMETRO (CD) PERPENDICULAR AL ANTERIOR AB. 4º.- ABATIR LAS DOS RECTAS ANTERIORES, DETERMINANDO MEDIANTE ORTOAFINIDAD EL ABATIMIENTO DE LOS PUNTOS (O), (A) Y (B). 5º.- TRAZAR LA CIRCUNFERENCIA ABATIDA DE CENTRO (O) Y DIÁMETRO (A)(B) DETERMINANDO EL DIÁMETRO PERPENDICULAR (C)(D). DESABATIR EL DIÁMETRO (C)(D) (RECTA DE MÁXIMA PENDIENTEU) OBTENIENDO LAS PROYECCIONES c'-c y d'-d. SOLUCIÓN: LAS PROYECCIONES DIÉDRICAS HORIZONTALES DE LOS DIÁMTEROS AB Y CD SON EJES DE UNA ELIPSE (PROYECCIÓN HORIZONTAL DE LA CIRCUNF.). LAS PROYECCIONES DIÉDRICAS VERTICALES DE LOS DIÁMTEROS AB Y CD SON DIÁMETROS CONJUGADOS DE UNA ELIPSE (PROYECCIÓN VERTICAL DE LA CIR