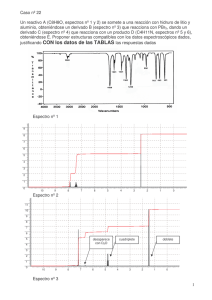
cap07 Análisis Espectral de Señales con FFT 12

Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
Análisis espectral de señales
periódicas con FFT
Contenido
Pg.
7.1
7.2
7.3
7.4
7.5
7.6
Introducción a la Transformada Discreta de Fourier
Uso de la Transformada Discreta de Fourier
Método de uso de la FFT
Cálculo de potencia en el dominio de la frecuencia
Cálculos de relación señal a ruido
Estimación del espectro de una señal aleatoria
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
3-3
3-5
3-8
3-12
3-12
3-13
2009
1
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
2
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
7.1. Introducción a la Transformada Discreta de Fourier
7.4.1. Transformada Discreta de Fourier
En matemáticas, la transformada Discreta de Fourier, designada con frecuencia por la abreviatura DFT (del
inglés Discrete Fourier Transform), y a la que en ocasiones se denomina transformada de Fourier finita, es
una operación ampliamente empleada en tratamiento de señales y en campos afines para analizar las
frecuencias presentes en una señal muestreada, resolver ecuaciones diferenciales parciales y realizar otras
operaciones, como convoluciones y correlaciones. La Transformada discreta de Fourier puede calcularse de
modo muy eficiente mediante el algoritmo FFT.
Hay dos situaciones a considerar en cuanto al uso de la Transformada Discreta de Fourier:
•
•
Sólo sirve para señales potencia del tipo periódico.
La mayoría de las señales a estudiar no son periódicas.
Considere ahora la secuencia de números complejos , , , , los cuales son muestras de una
señal analógica. Tal secuencia debe transformarse en la secuencia de números complejos , , , , las cuales son muestras del espectro de la señal analógica, según la fórmula:
;
Siendo:
•
•
•
•
0, , 1
(7.1)
la base de los logaritmos naturales,
la unidad imaginaria ( 1)
es el número de muestras.
Esta transformada se denota de forma común mediante el símbolo ,
La transformada de Fourier discreta inversa (por sus siglas en inglés IDFT, Inverse Discrete Fourier
Transform) se calcula, por otra parte, mediante:
1
;
0, , 1
(7.2)
Siendo que
•
•
el número de muestras
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
3
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
7.4.2. Transformada Rápida de Fourier
FFT es la abreviatura usual (del inglés Fast Fourier Transform) de un algoritmo eficiente que permite calcular
la Transformada Discreta de Fourier (DFT) y su inversa. Así entonces, consideremos nuevamente la
secuencia de números complejos , , , , la cual debe transformarse en la secuencia de números complejos , , , según la fórmula en la ecuación (7.1).
La evaluación directa de esa fórmula requiere !" # operaciones aritméticas. Mediante un algoritmo FFT se
puede obtener el mismo resultado con sólo !" $%& # operaciones. En general, dichos algoritmos
funcionan para una , potencia de 2. Aunque también existen versiones menos rápidas para cualquier par.
La idea que permite esta optimización es la descomposición de la transformada a tratar en otras
transformadas más simples y éstas a su vez en otras más simples hasta llegar a transformadas de 2
elementos " 2#. Una vez resueltas las transformadas más simples hay que agruparlas en otras de nivel
superior que deben resolverse de nuevo y así sucesivamente hasta llegar al nivel más alto. Al final de este
proceso, los resultados obtenidos deben reordenarse.
Dado que la Transformada Discreta Inversa de Fourier es análoga a la Transformada Discreta de Fourier, con
distinto signo en el exponente y un factor 1/, cualquier algoritmo FFT puede ser fácilmente adaptado para
el cálculo de la transformada inversa.
7.4.3. FFT y Matlab
Matlab permite el cálculo de la FFT para una secuencia de muestras de señal contenidas en un vector. Una
forma simple de uso es como sigue:
t=0:0.003/(512-1):0.003;
X=sin(2*pi*1000*t);
F=fft(X);
magnitude=abs(F);
%magnitud del espectro
plot(magnitude);
7.4.4. Aplicaciones
Algunas aplicaciones que definen a la FFT son:
•
•
•
•
•
•
•
•
•
Compresión de imagen y audio.
Filtrado digital.
Reducción de ruido en señales, como el ruido blanco.
Resolución de ecuaciones diferenciales parciales.
Análisis en frecuencia de cualquier señal discreta, ya sea periódicas o aperiódicas.
Análisis de materiales y estadística.
Síntesis, mediante la transformada inversa IFFT.
Algoritmos rápidos de convolución y correlación
Detección de movimiento
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
4
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
7.4.5. Teorema de muestreo de Nyquist
Este teorema puede expresarse tanto en el dominio del tiempo como en el de la frecuencia. Así entonces.
Teorema de Nyquist en el dominio del tiempo. Sea una señal sin componentes espectrales mayores a
)*+ ,-./, ésta queda determinada en forma única por sus valores en intervalos uniformes menores o
iguales a 1⁄2)*+ .
Teorema de Nyquist en el dominio de la frecuencia. La rapidez de muestreo 1 de una señal es por lo menos
el doble de la frecuencia máxima contenida en la señal ")*+ #: 1 2 2)*+ .
7.2. Uso de la Transformada Discreta de Fourier
Consideremos una señal periódica de la que se toma un espacio muestral con cardinalidad de en un
periodo de duración 3 tal como se ilustra en la figura 1.
Fig01
Figura 1
Según la figura
•
•
•
3 periodo de la señal
es el número de muestras
6
45 periodo de muestreo
De la figura 1, note que la muestra no forma parte del espacio muestral que se pretende analizar ya que
corresponde al siguiente periodo de la señal.
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
5
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
Luego se aplica la operación DFT a la señal. Para entender el significado del resultado, debe considerarse
que el espectro de una señal discreta y periódica es también discreto y periódico. La figura 2 ilustra un
periodo de tal espectro.
Figura 2. Espectro prototipo. El espectro consta de un número par de muestras.
De la figura 2 podemos establecer las siguientes relaciones
•
•
•
1 1⁄41 : frecuencia de muestreo
7 resolución frecuencial.
1 ⁄2 es la frecuencia máxima con significado en el espectro.
Note que:
•
•
La frecuencia máxima que se calcula en el espectro es 5 "1 1⁄# y no 5 debido a que esta última
frecuencia corresponde con el siguiente periodo del espectro: recuerde que el espectro es
periódico.
La frecuencia máxima con significado en el espectro es 5 ⁄2 . Esta frecuencia no es la frecuencia
máxima de la señal.
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
6
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
7.2.1. Periodicidad del espectro
La DFT es una operación para señales discretas periódicas, en consecuencia, el espectro es discreto y
periódico. Así entonces, el espectro de alguna señal que se ve en la figura 2 es sólo parte del espectro
mostrado en la figura 3.
Figura 3.
7.2.2. Corrección del espectro
La DFT, calculada a través de la FFT, nos genera un espectro como el de la figura 2. Podemos aprovechar la
periodicidad y simetría de que caracteriza a la DFT para generar un espectro como el mostrado en la figura
4, lo cual es más acorde con lo que esperamos ver.
Figura 4.
En Matlab, para lograr un espectro como el mostrado en la figura 4, se usa la función 89:;8. El siguiente
ejemplo ilustra el uso de la función:
t=0:0.003/(512-1):0.003;
X=sin(2*pi*1000*t);
F=fftshift(fft(X));
magnitude=abs(F);
%magnitud del espectro
plot(magnitude);
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
7
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
7.2.3. Factor de ajuste
Luego de aplicar el algoritmo de FFT, para obtener espigas con magnitudes que correspondan a la teoría, se
debe considerar un factor de ajuste:
GE8%D 7 GF98 1
(7.3)
En resumen, tenemos una nueva versión de la Transformada Discreta de Fourier, la cual está dada por
GE8%D_LF98 M 8"#
(7.4)
Donde
•
•
, , , Secuencia de muestras de una señal en el dominio del tiempo
, , , Secuencia de muestras del espectro de la señal.
7.3. Método de uso de la FFT con MATLAB
La FFT, aunque efectiva, no es una herramienta fácil de usar. Los siguientes pasos son una receta que puede
ser útil:
Paso 1: Se requieren de dos datos previos para preparar el cálculo de la DFT. El primer dato es la frecuencia
máxima contenida en el mensaje
)*+ ¿ ?
El segundo dato previo es el número de muestras de la señal. Este debe ser potencia de 2. Por lo general se
prefiere trabajar con 8192, 16384, 32768 o 65536 muestras:
8192
Paso 2: Calcule los parámetros espectrales:
5
@ 2ABC
7
MI. Mario Alfredo Ibarra Carrillo
5
DEF E;G 7 HF98D%
I9%$FE;ó DEF E;G$
[Escribir texto]
2009
8
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
Paso 3: Calcule parámetros temporales
1
5
45
3
45
ND;%7% 7 HF98D% 8HO%DG$
PFDGE;% 7$ 9OGE;% HF98DG$ 8HO%DG$
Paso 4: En el dominio del tiempo, calcule el vector de instantes de muestreo y la señal. La señal "8# puede
ser capturada por micrófono o generada por alguna ecuación: las muestras se almacenan en el vector .
8
1
0: 45 : 3 R1 S T 7$ 8;HO% % 7%H; ;% 8HO%DG$
"8#
F E;ó 7$ 8;HO%
Paso 5: En el dominio de la frecuencia, calcule el vector de frecuencias en hertz y el espectro
-.
5
5
1
: 7: R1 S
2
2
T 7 $G DEF E;G % 7%H; ;% 9OE8DG$
1
89:;8 U 8"#V T9OE8D% 7 $G 9ñG$ "9%$% HG& ;8F7#
Paso 6: Grafique la señal en el dominio del tiempo. A esta gráfica se le suele conocer vulgarmente como el
oscilograma.
;&FD"1#
O$%8"8, #
8;8$"X!9E;$%&DGHGX#
Es posible que el oscilograma se exhiba como un manchón, es decir, hay demasiadas muestras, tantas que
saturan el oscilograma. Para observar un fragmento de la señal graficada use la función axis antes de la
función title:
G;9",8H; 8HG YH; YHG/#
Donde 8H; 8HG especifican los límites temporales entre los cuales se visualiza la señal. Los valores
YH; YHG son los límites en magnitud entre los cuales se grafica la señal.
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
9
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
Paso 7: Grafique el espectro de la señal.
;&FD"2#
O$%8"-., GZ9"##
8;8$"XT9OE8D%X#
Observe el uso de la función GZ9" #. Esta función es necesaria ya que las muestras del espectro son
números complejos y sólo se desea exhibir la magnitud de tales.
Es posible que el espectro se exhiba como un pequeño manchón en el centro de la gráfica, es decir, el
espectro está concentrado en una pequeña banda de frecuencias. Para observar sólo esa banda de
frecuencias use la función axis:
G;9",H;
HG
0 .HG/#
Al usar la función axis para exhibir sólo frecuencias positivas, el espectro debe multiplicarse por un factor de
dos. A consecuencia, el código para exhibir el espectro de una señal, con sólo las frecuencias positivas,
queda como:
;&FD"2#
O$%8"-., 2 [ GZ9"##
G;9",H;
HG
8;8$"XT9OE8D%
MI. Mario Alfredo Ibarra Carrillo
\#
0 .HG/#
[Escribir texto]
2009
10
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
7.3.1. Ejemplo: Senoide
Calcule el espectro de una señal sinusoidal de 1000Hz. El equipo tiene capacidad para almacenar 256
puntos. Use una frecuencia de muestreo de 16 veces la frecuencia máxima.
% 1) La frecuencia máxima en la señal
fmax=1000;
% 2 El número de muestras
N=256;
% 3) Parámetros espectrales
fs=16*fmax;
df=fs/N;
% 4) Parámetros temporales
ts=1/fs;
T=N*ts;
% 5) Cálculo de la función senoidal
t=0:ts:T*(1-1/N);
X=sin(2*pi*1000*t);
% 6) Cálculo del espectro
fHz=-0.5*fs : fs/N : 0.5*fs*(1-1/N); %frecuencia en Hz
F=fftshift(fft(X)/N);
% 7) Oscilograma
figure(1)
subplot(2,1,1);
plot(t,X);
axis([0 0.003 -2 2]) % Se grafican 3ms de la señal o tres ciclos
title('Osciloscopio')
% 8) Espectro
subplot(2,1,2);
stem(fHz,abs(F));
axis([-2000, 2000, 0, 1])
title('Analizador de espectros')
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
11
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
La figura generada es:
Domino del tiempo
2
1
0
-1
-2
0
0.5
1
1.5
2
2.5
3
-3
x 10
1
0.5
0
-2000
-1500
-1000
-500
0
500
1000
1500
2000
Figura 5.
Observe que las amplitudes de las espigas son de 0.5,_/, esto es porque se cumple con una de las formas del
teorema de Parseval:
O%8 E;G
7 9ñG$
7%H; ;%
8;HO%
O%8 E;G
7 9ñG$
7%H; ;%
9OE8D%
Expresado en otra forma, se tiene que:
MI. Mario Alfredo Ibarra Carrillo
` `
(7.5)
[Escribir texto]
2009
12
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
7.3.2. Ejemplo: dos senoides
Calcule el espectro de:
9; "2a10008# b 29; "2a15008#
(7.6)
El equipo tiene capacidad para almacenar 256 puntos. Use una frecuencia de muestreo de 16 veces la
frecuencia máxima.
% 1) La frecuencia máxima en la señal
fmax=1000;
% 2 El número de muestras
N=256
% 3) Parámetros espectrales
fs=16*fmax;
df=fs/N;
% 4) Parámetros temporales
ts=1/fs;
T=N*ts;
% 5) Cálculo de la función senoidal
t=0:ts:T*(1-1/N);
X=sin(2*pi*1000*t) + 2*sin(2*pi*1500*t);
% 6) Cálculo del espectro
fHz=-0.5*fs : fs/N : 0.5*fs*(1-1/N); %frecuencia en Hz
F=fftshift(fft(X)/N);
% 7) Oscilograma
figure(1)
subplot(2,1,1);
plot(t,X);
axis([0 0.003 -3 3]) % Se grafican 3ms de la señal o tres ciclos
title('Osciloscopio')
% 8) Espectro
subplot(2,1,2);
stem(fHz,abs(F));
axis([-2000, 2000, 0, 2])
title('Analizador de espectros')
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
13
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
La figura generada es:
Domino del tiempo
2
0
-2
0
0.5
1
1.5
2
2.5
3
-3
x 10
Domino de la frecuencia
2
1.5
1
0.5
0
-2000
-1500
-1000
-500
0
500
1000
1500
2000
Figura 6.
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
14
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
7.3.3. Ejemplo: Desplazamiento en frecuencia
En este ejemplo vamos a comprobar una de las propiedades de la transformada de Fourier. La propiedad a
verificar es la traslación en frecuencia, es decir
"8# cd e "f f #
(7.7)
Este ejemplo consta de un desplazamiento a la derecha de 500Hz
9; "2a10008# ge
(7.8)
El equipo tiene capacidad para almacenar 256 puntos. Use una frecuencia de muestreo de 16 veces la
frecuencia máxima.
% 1) La frecuencia máxima en la señal
fmax=1000;
% 2 El número de muestras
N=512;
% 3) Parámetros espectrales
fs=16*fmax;
df=fs/N;
% 4) Parámetros temporales
ts=1/fs;
T=N*ts;
% 5) Cálculo de la función senoidal
t=0:ts:T*(1-1/N);
X=sin(2*pi*1000*t).*exp(i*2*pi*500*t);
% 6) Cálculo del espectro
fHz=-0.5*fs : fs/N : 0.5*fs*(1-1/N);
F=fftshift(fft(X)/N);
% 6) Oscilograma
figure(1)
subplot(2,1,1);
plot(t,abs(X));
axis([0 0.003 -2 2]) % Se grafican 3ms de la señal o tres ciclos
title('Domino del tiempo')
subplot(2,1,2);
stem(fHz,abs(F));
axis([-2000, 2000, 0, 1])
title('Domino de la frecuencia')
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
15
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
La gráfica generada tiene la forma
Domino del tiempo
2
1
0
-1
-2
0
0.5
1
1.5
2
2.5
3
-3
x 10
Domino de la frecuencia
1
0.5
0
-2000
-1500
-1000
-500
0
500
1000
1500
2000
Figura 7.
Observe que la gráfica del dominio del tiempo aparece rectificada debido a la función “abs()”.
La propiedad de desplazamiento en frecuencia afecta espectralmente a la señal y no la afecta en el dominio
del tiempo.
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
16
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
7.4. Cálculo de potencia
7.4.1. En el dominio del tiempo
El cálculo de la potencia de una señal continua y periódica, en el dominio del tiempo, queda expresado en la
ecuación 7.9
`"8# 1
i "8#78
3
(7.9)
6
Pero si la señal se discretiza, debemos discretizar la respectiva ecuación considerando las siguientes
relaciones
8
78
3
45
45
(7.10)
45
Así nos queda que la potencia de la señal se puede aproximar como:
`"8# h
1
" 41 #41
41
(7.11)
Dado que las muestras de "8# se almacenan en un vector , . . , , . . , , podemos escribir
1
`"8# h
41
41
(7.12)
Resolviendo los términos comunes
1
`"8# h MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
(7.13)
2009
17
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
Donde
•
•
es la n-ésima muestra.
es el número de muestras de la señal y dado que la señal se almacena en un vector, tal número
se consigue con la función MATLAB $ &8:"#.
Finalmente, dado que trabajamos ahora con un vector de muestras, , podemos expresar la potencia de tal
vector como sigue:
1
` (7.14)
Al estilo de MATLAB, hacemos
` 9FH".[ #/
(7.15)
Donde
•
•
es el vector renglón que contiene a las muestras de la señal.
es el número de muestras de la señal.
7.4.2. En el dominio de la frecuencia
El espectro de una señal quedó definido en la ecuación (7.4). Si se aplica inmediatamente el factor, de
ajuste, la ecuación resulta en:
1
8"#
(7.16)
Donde:
•
es el vector de muestras del espectro: , , , j , , El cálculo de potencia en la frecuencia, mediante la Transformada Discreta de Fourier, recordando que es
para señales discretas y periódicas, se calcula en el dominio de la frecuencia como:
` [
(7.17)
[Escribir texto]
2009
MI. Mario Alfredo Ibarra Carrillo
18
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
La ecuación 7.17, en el estilo de MATLAB queda como:
` 9FH".[ E% "##
(7.18)
Donde
•
•
es un vector que contiene las muestras del espectro.
E% "# es un vector que contiene las muestras conjugadas del espectro: las muestras del espectro
son números complejos.
7.4.3. Teorema de Parseval
El respectivo teorema de Parseval relaciona los cálculos de potencia en los dominios discretos del tiempo y
de la frecuencia de la forma siguiente:
` `
(7.19)
7.4.4. El código para cálculo de la potencia en el dominio de la frecuencia
%signal=<capturada o generada>
F=fftshift( fft(X)/lneght(X) ) ;
SF=sum(F.*conj(F));
7.5. Cálculos de relación señal a ruido
La Relación Señal a Ruido es factor que indica la calidad de una señal en alguna de las etapas de un sistema
de comunicación. Esta relación se define como:
I`I `9ñG$ N%8 E;G 7 9ñG$
`DF;7% N%8 E;G 7 DF;7%
(7.20)
En muchos experimentos sólo podemos medir
•
•
`9ñG$
`9ñG$ b DF;7%
Como observa, no se cuenta con la capacidad de medir directamente la potencia del ruido involucrado. Para
medir esta cantidad podemos considerar la siguiente relación, la cual se deriva del teorema de Parseval.
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
19
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
`9ñG$ b DF;7% `9ñG$ b `DF;7%
(7.21)
Sustituyendo esta relación de la ecuación 7.21 en la ecuación 7.20 resulta:
I`I `9ñG$
`9ñG$ b DF;7% `9ñG$
(7.22)
7.6. Estimación del espectro de una señal aleatoria
7.6.1. Teorema de equivalencia espectral de Maic
La DFT sólo es útil para señales discretas periódicas. Al respecto, ¿Qué pasa con las señales que son
aleatorias? Una forma de estudiar estas señales es mediante dos consideraciones:
a.
b.
Se obtiene un espacio muestral de la señal aleatoria y se considera que esta ventana es periódica.
Aplique el siguiente teorema: “El contenido espectral de la señal aleatoria es igual al contenido
espectral de la correlación cruzada promediada de tal señal consigo misma”. Este teorema es válido
cuando la curva de correlación sea una función causal y del tipo energía.
Las dos consideraciones pueden anotarse en forma de ecuación de la siguiente forma:
k`
h
[[ (7.23)
k` [[ Donde
•
•
•
•
•
es el vector de muestras de la señal.
` es la potencia de la señal en tiempo continuo calculada a partir de sus muestras.
[[ E%DD", XF Z;G97X#; es la correlación promediada es insesgadandel vector de muestras
consigo mismo.
` [[ es la potencia de la función que resulta de la correlación.
[[ es el espectro de la correlación: [[ 89:;8"8" [[ #/$ &8:" [[ #
Este teorema en forma de la ecuación 7.23 permite calcular, de forma aproximada, el espectro de una señal
cualquiera a partir de su correlación promediada, ecuación siguiente:
X MI. Mario Alfredo Ibarra Carrillo
k`
k` [[ [Escribir texto]
[[ (7.24)
2009
20
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
Si comparamos el cálculo de las potencias de los espectros definidos por las ecuaciones 7.16 y 7.24,
tendremos la siguiente relación
` `X
(7.25)
h X
(7.26)
No obstante que las magnitudes de las espigas entre y X son ligeramente diferentes:
7.6.2. Cálculo del espectro de una señal aleatoria
Los pasos que siguen nos indican cómo calcular el espectro.
1.
Capturar una muestra de una señal aleatoria. Es buena idea si el número de muestras es par y es aún
mejor idea si el número de muestras es una potencia de 2. La figura 8 ilustra un registro temporal u
oscilograma, de la palabra manzana.
0.015
0.01
0.005
0
-0.005
-0.01
-0.015
-0.02
0
200
400
600
800
1000
1200
Figura 8.
2.
Se obtiene la correlación cruzada promediada de tal muestra consigo misma. Úsese la función MATLAB
xcorr con el parámetro ‘unbiassed’, es decir, calcule una correlación sin errores de aproximación. La
figura 9 muestra la correlación cruzada de la señal consigo misma. Se puede observar que la curva de
correlación cruzada es simétrica y es de tipo energía.
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
21
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
0.025
0.02
0.015
0.01
0.005
0
-0.005
0
0.5
1
1.5
2
2.5
3
3.5
4
x 10
Figura 9.
3.
4.
Grafique la curva de correlación. Si esta curva parece ser del tipo energía, entonces proceda con el paso
4, de otra forma, termina. La gráfica anterior ilustra perfectamente una curva de correlación cruzada del
tipo energía ya que concentra sus cambios en un pequeño intervalo.
Extrae la mitad derecha de la curva de correlación: esta mitad corresponde con una función del tipo
causal. La figura 10 muestra que se ha extraído la mitad derecha de la curva de correlación cruzada. Esta
mitad corresponde con una señal de causal y de tipo energía.
0.025
0.02
0.015
0.01
0.005
0
-0.005
0
2000
4000
6000
8000
10000 12000 14000 16000
18000
Figura 10.
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
22
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
5.
Calcula de FFT de la curva de correlación. La gráfica está acotada en hertz y en valores pico.
0.025
0.02
0.015
0.01
0.005
0
-4000
-3000
-2000
-1000
0
1000
2000
3000
4000
Figura 8.
El código siguiente es una función que captura voz mediante un micrófono conectado a la laptop. Este
código funciona con palabras cortas como “manzana”.
function xpectrum(level)
%Parámetros de la señal
fs=8000; %sample frec.
N=16384;
%num. Samples
ts=1/fs;
T=N*ts;
input('Presione tecla para grabar voz')
onda=level*wavrecord(N,fs,1,'double');
disp('registrado')
figure(1)
plot(onda(1000:2000));
rxx=xcorr(onda,'unbiased');
figure(2)
plot(rxx)
rxx=rxx(ceil(0.5*length(rxx)):length(rxx));
figure(3)
plot(rxx)
onda_pow=sum(onda.*onda)/length(onda);
spec=fft(rxx)/length(rxx);
spec_pow=sum(spec.*conj(spec));
spectrum=sqrt(onda_pow/spec_pow)*abs(fftshift(spec));
f=-0.5*fs:fs/N:0.5*fs*(1-1/N);
figure(4)
plot(f,spectrum)
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
23
Sistemas de Comunicaciones
Capítulo 7. Análisis Espectral de Señales periódicas con FFT
Apéndice A. Generación de señales en MATLAB
La señal cuadrada
Para generar una señal cuadrada se usa la función square, la cual tiene las siguientes formas:
9lFGD "m#
9lFGD "m, 7F8Y#
Donde:
•
•
•
mn,0,2a/ para un solo ciclo.
7F8Y es el ciclo de trabajo expresado en porcentaje de 0 a 100.
La amplitud de la señal cuadrada varía de 1 a 1.
Para generar un tren de pulsos, basta con seguir la siguiente fórmula
L
¿?
; T9 $G GHO$;8F7 7$ 8D 7 OF$9%9
1
1
[ L [ 9lFGD"m, 7F8Y# b [ L ; 3D 7 OF$9%9
2
2
La señal diente de sierra
Para generar una señal diente de sierra se usa la función sawtooth, la cual tiene las siguientes formas:
9Go8%%8: "m#
9Go8%%: "m, 7F8Y#
Donde:
•
•
•
mn,0,2a/.
o;78: es el factor de simetría cuyo valor varía de de 0 a 1. Un valor de 0.5 genera una función
triangular.
La amplitud de la señal cuadrada varía de 1 a 1.
MI. Mario Alfredo Ibarra Carrillo
[Escribir texto]
2009
24