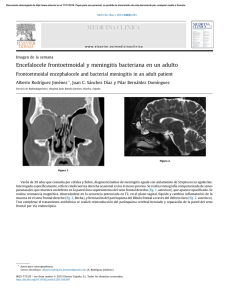
Procesos Estocásticos - OCW
Anuncio

Cadenas de Markov a tiempo continuo
Definición
Para extender la propiedad de Markov a tiempo continuo se requiere
definir la probabilidad condicional dado que conocemos el proceso en un
intervalo continuo [0, s] del tiempo, es decir, condicionar respecto a
eventos del tipo {Xt , 0 ≤ t ≤ s}.
Decimos que el proceso estocástico {Xt , t ≥ 0} es una Cadena de
Markov a tiempo continuo si para cualesquiera instantes del tiempo
0 ≤ s0 < s1 < . . . sn < s y cualquier conjunto de estados i0 , . . . , in , i, j se
verifica
P(Xt+s = j|Xs = i, Xsn = in , . . . , Xs0 = i0 ) = P(Xt+s = j|Xs = i)
Esto es, dado el presente, cualquier otra información pasada del proceso es
redundante para hacer pronósticos del futuro.
Raúl Jiménez y Rosario Romera (UC3M)
Procesos Estocásticos
Diciembre 2008
1 / 11
Cadenas de Markov a tiempo continuo
Ejemplo
Sea {N(t), t ≥ 0} el proceso de Poisson con intensidad constante λ y {Yn }
un CM a tiempo discreto con matriz de transición P. Entonces, el proceso
definido por Xt = YN(t) es una cadena de Markov a tiempo continuo.
Si S1 , S1 , . . . son los momentos de renovación del proceso N(t), entonces
{X0 , XS1 , . . .} es una CM a tiempo discreto con la misma ley que {Yn }
dado Y0 = X0 . Los tiempos transcurridos (Ti = Si − Si−1 ) entre los
instantes de actualización del proceso Xt son variables i.i.d exponenciales.
La propiedad de pérdida de memoria de la distribución exponencial es la
clave para que la cadena descrita sea de Markov.
La probabilidad de transición de esta cadena es
P(Xt = j|X0 = i) =
X
e −λt
n≥0
Raúl Jiménez y Rosario Romera (UC3M)
Procesos Estocásticos
(λt)n n
p (i, j)
n!
Diciembre 2008
2 / 11
Cadenas de Markov a tiempo continuo
Probabilidades y tasas de transición
Como en el caso discreto, supondremos que la cadena es homogénea,
P(Xs+t = j|Xs = i) = P(Xt = j|X0 = i)
y llamaremos matriz de probabilidades de transición a la matriz Pt con
componente i, j definida por
[Pt ]i,j = pt (i, j) = P(Xt = j|X0 = i)
Las probabilidades de transición satisfacen las ecuaciones de
Chapman-Kolmogorov, que para el caso continuo son
X
ps+t (i, j) =
ps (i, k)pt (k, j)
k
Definimos tasa de transición de i a j, y la denotamos por q(i, j), al valor
pt (i, j)
t
t→0
el cual se interpreta como la intensidad con que la cadena salta de i a j.
q(i, j) = lim+
Raúl Jiménez y Rosario Romera (UC3M)
Procesos Estocásticos
Diciembre 2008
3 / 11
Cadenas de Markov a tiempo continuo
Construcción de la CM a partir de las tasas de transición
La tasa con la cual la cadena deja el estado i la denotamos por λi :
X
λi =
q(i, j)
j6=i
Decimos que un estado i es absorbente si λi = 0, estable si 0 < λi < ∞ e
instantáneo si λi = ∞. La cadena deja los estados instantáneos de forma
inmediata, ası́ que siempre asumiremos λi < ∞. Si λi > 0 definimos las
probabilidades de transición
r (i, j) = q(i, j)/λi
Si X (s) = i y el estado i es absorbente, la cadena permanecerá en i por
siempre. Por el contrario, si el estado es estable, la cadena permanecerá en
i un tiempo distribuı́do exponencialmente con tasa λi y luego saltará a
otro estado con probabilidad de transición r (i, j). Usando recursivamente
este procedimiento construı́mos la cadena.
Raúl Jiménez y Rosario Romera (UC3M)
Procesos Estocásticos
Diciembre 2008
4 / 11
Cadenas de Markov a tiempo continuo
Ecuaciones diferenciales de Kolmogorov
Hemos discutido como a partir de las tasas de transición podemos
construir la cadena a tiempo continuo. Ya que la cadena está determinada
por las probabilidades de transición, entonces deberı́amos poderlas calcular
estas últimas a partir de las tasas de transición. La formalización de esta
construcción se expresa en el siguiente resultado:
Teorema 1. Supongamos que ningún estado es instantáneo. Entonces, las
probabilidades de transición son diferenciables en t y para cualquier par de
estados i, j se tiene
X
dpt
(i, j) =
q(i, k)pt (k, j) − λi pt (i, j) Backward equation
dt
k6=i
X
dpt
(i, j) =
q(k, j)pt (i, k) − λj pt (i, j) Forward equation
dt
k6=j
Raúl Jiménez y Rosario Romera (UC3M)
Procesos Estocásticos
Diciembre 2008
5 / 11
Cadenas de Markov a tiempo continuo
Comportamiento asintótico
Para el estudio asintótico de las cadenas de Markov a tiempo continuo no
requerimos la condición de aperiodicidad. Vamos a definir algunos
conceptos para el caso continuo antes de enunciar los resultados más
importantes.
1
Una cadena continua es irreductible si puede saltar de un estado a
otro en un número finito de saltos. Más formalmente, para todo par
de estados i, j existe una sucesión finita de estados
i = k1 , k2 , . . . , kn , kn+1 = j con q(km , km+1 ) > 0 para todo
1 ≤ m ≤ n.
2
Llamamos generador infinitesimal de la cadena a la matriz Q
definida por
q(i, j) si j 6= i
Q(i, j) =
−λi
si j = i
Raúl Jiménez y Rosario Romera (UC3M)
Procesos Estocásticos
Diciembre 2008
6 / 11
Cadenas de Markov a tiempo continuo
Distribución estacionaria
Decimos que π es una distribución estacionaria si para todo t > 0 es una
solución de π = πPt . O bien, elemento a elemento, sipara todo j y t > 0
X
π(j) =
π(i)pt (i, j)
i
Verificar por definión que una función de probabilidad es una distribución
estacionaria es en general difı́cil ya que, por un lado, tiene que cumplirse
π = πPt para todo t > 0 y, por otro, el cálculo de Pt puede ser
complicado. El siguiente teorema resuelve el problema.
Teorema 2. π es una distribución estacionaria para la cadena sii satisface
la ecuación de balance πQ = 0. O lo que es lo mismo, si y sólo si
X
π(i)q(i, j) = λj π(j)
i6=j
Raúl Jiménez y Rosario Romera (UC3M)
Procesos Estocásticos
Diciembre 2008
7 / 11
Cadenas de Markov a tiempo continuo
Teorema de convergencia
Al igual que en el caso discreto, de existir una distribución estacionaria, la
cadena la alcanza asintóticamente, con indepencia de la distribución
inicial. Es por ello que la distribución estacionaria es un objeto clave en el
estudio de modelos markovianos:
Teorema 3. Supongamos que la cadena a tiempo continuo {Xt , t > 0} es
irreductible y que tiene distribución estacionaria π. Entonces,
lim pt (i, j) = π(j)
t→∞
Adicionalmente, si G (i)
P es la ganancia obtenida cada vez que la cadena
alcanza el estado i y j |G (j)|π(j) < ∞, se tiene
1
t
Z
t
G (Xs )ds →
0
Raúl Jiménez y Rosario Romera (UC3M)
X
G (j)π(j), cuando t → ∞
j
Procesos Estocásticos
Diciembre 2008
8 / 11
Cadenas de Markov a tiempo continuo
Condición de balance detallado
Decimos que π satisface una condición de balance detallado si
πi q(i, j) = π(j)q(j, i), para todo par de estados i, j
(1)
sumando sobre todos los estados i 6= j, de la ecuación anterior resulta
X
X
πi q(i, j) = λj πj ⇒
πi q(i, j) − λj πj = [πQ]j = 0
i6=j
i6=j
Es decir, si π satisface (1) entonces satisface la ecuación de balance
πQ = 0 y en consecuencia es una distribución estacionaria.
Las ecuaciones de balance detallado (1) son en general sencillas de
resolver y se satisfacen para muchos modelos importantes.
Raúl Jiménez y Rosario Romera (UC3M)
Procesos Estocásticos
Diciembre 2008
9 / 11
Cadenas de Markov a tiempo continuo
Cadenas de nacimiento y muerte
Consideremos la cadena a tiempo continuo con espacio de estados
{0, 1, . . . } con
λi para j = i + 1
q(i, j) = µi para j = i − 1
0 para |j − i| > 1
El proceso se denomina de nacimiento y muerte, λn representa la tasa
de nacimiento y µn la tasa de muerte cuando hay n individuos.
Las ecuaciones de balance detallado de la cadena de nacimiento y muerte
son
π(n − 1)λn−1 = π(n)µn , para n ≥ 1
Usando recurrencia se obtiene
π(n) =
Raúl Jiménez y Rosario Romera (UC3M)
λn−1 λn−2 · · · λ0
π(0)
µn µn−1 · · · µ1
Procesos Estocásticos
Diciembre 2008
10 / 11
Cadenas de Markov a tiempo continuo
Ejemplos de Colas
1
M/M/1. Es la cola en un sistema con un servidor, tiempos entre
llegadas exponenciales con tasa λ y tiempos de servicio exponenciales
con tasa µ. Corresponde a un proceso de nacimiento y muerte con
λn = λ y µn = µ. Si la tasa de tráfico ρ = λ/µ < 1, su distribución
estacionaria es la distribución geométrica desplazada
π(n) = (1 − ρ)ρn para n ≥ 0
2
M/M/s. El mismo caso que antes pero con s servidores. Es el
proceso de nacimiento y muerte con λn = λ y
nµ 1 ≤ n ≤ s
µn =
sµ
n>s
Si ρ < s la cola tiene una distribución estacionaria que satisface
n+1
λ
π(s + n) =
π(s − 1)
sµ
Raúl Jiménez y Rosario Romera (UC3M)
Procesos Estocásticos
Diciembre 2008
11 / 11




![Práctico 2 - parte 1 1. ([2], p.8) Sea {X n}n≥0 una cadena de Markov](http://s2.studylib.es/store/data/005434198_1-4a9a3e72fcacb76f6647ccd064de45bd-300x300.png)