CRECIMIENTO y DESARROLLO Clase 2 Modelo de Solow 2012

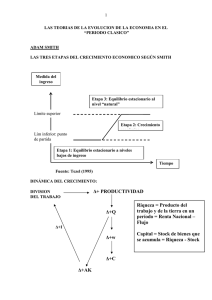
CRECIMIENTO y
DESARROLLO
Clase 2
Modelo de Solow
2012
La visión neoclásica de la
innovación tecnológica: la función
de producción
a nivel
microeconómico
Función de producción de la
empresa: tecnología
Mapa de isocuantas: tecnología
las técnicas y el cambio técnico
Técnica/ Tecnología
cambio técnico/cambio
tecnológico
Tecnología:
Técnica: K/L
Mapa de
iscuantas
(función de
producción)
Elección técnica
Rendimientos marginales
LEY DE RENDIMIENTOS MARGINALES
DECRECIENTES: un factor queda constante
• Cuando los recursos de capital son fijos, a
medida que se vayan agregando
trabajadores adicionales (marginales) al
proceso de producción, la productividad
laboral a la larga disminuirá, a pesar de
que aumenta la producción total
Rendimientos de escala
• Todos los factores aumentan en la misma proporción
cuánto aumenta la cantidad producida
• Rendimientos constantes a escala
f(kx1,kx2)= kf(x1, x2)
• Rendimientos crecientes a escala
f(kx1,kx2)> kf(x1, x2)
• Rendimientos decrecientes a escala
f(kx1,kx2)< kf(x1, x2)
Economías (deseconmías) de escala es cuando los
rendimientos crecientes se traducen en costos
decrecientes (crecientes)
A nivel
macroeconómico
"A Contribution to the Theory of Economic Growth",
Quarterly Journal of Economics, febrero, 1956.
Objetivo:
•
Solow quiere mostrar cómo se puede dar un
crecimiento equilibrado de pleno empleo si se
cumplen los siguientes requisitos:
1.
La asignación de los recursos se hace por medio
del mercado⇒ se maximiza la eficiencia y el
bienestar (óptimo de Pareto)
2.
Los precios son las variables de ajuste que
llevan al punto de equilibrio. El crecimiento
equilibrado lleva a términos dinámicos el
equilibrio general de la teoría estática de
Walras.
• Solow utiliza una función de
producción agregada
neoclásica como instrumento
para explicar el crecimiento:
Y=F(K,L) (L: trabajo y
K:capital)
Hipótesis del modelo
a) Los empresarios son maximizadores y tomadores de precios
(competencia perfecta).
b) Se utiliza una función de producción agregada como instrumento para
explicar el crecimiento:
Y=F(K,L) (L: trabajo y K: capital)
Intensidad capitalística (K/L):La función de producción permite la
sustituibilidad entre el capital y el trabajo
F(K,L) es una función homogénea de grado uno (exhibe rendimientos
constantes de escala (RCE)
F(K,L) exhibe productos marginales positivos y decrecientes: ley de la
productividad marginal decreciente
c) Cumple con el teorema de Euler: en equilibrio la empresa paga por cada
factor el valor de sus productividades marginales y eso agota
completamente el producto: Y=wL+iK (w=salarios; i=intereses)
d) El equilibrio se obtiene al mismo tiempo:
en el mercado de factores, a raíz de la hipótesis de sustituibilidad de los
factores de producción y flexibilidad de los precios.
en el mercado de los productos, a raíz de la hipótesis de igualdad entre la
inversión (I) y el ahorro (sY) (economía cerrada).
e) n>0 es la tasa de crecimiento del trabajo y es exógena; s>0 es la tasa de
ahorro y es exógena ; d>0 es la tasa de depreciación del capital y es
exógena.
¿Cómo se produce el crecimiento?
las fuentes de crecimiento del PIB son:
1. aumento de la fuerza de trabajo (L)
= n: es exógeno a la economía
2. aumento del stock de capital
(acumulación de K): el modelo de
crecimiento de Solow explica cómo
se produce esto.
F(K,L) en términos per cápita: y=F(k); en donde k=K/L
(cociente capital-trabajo) e y=Y/L (es el producto per cápita)
partiendo de que I=S y haciendo cuentas:
La ecuación fundamental:
∆k = sy-(n+d)k
• el ahorro debe financiar todo aumento de capital; el que se
necesita para reemplazar el que se deprecia, el que se necesita
para equipar a la nueva mano de obra y finalmente el que se
utiliza para aumentar la relación K/L
• se llama ampliación del capital al que se destina a nk
• se llama reemplazo del capital al que se destina a dk
• se llama profundización del capital al que se destina a
∆k⇒acumulación del capital
y
(n+d). k
y = f(k)
BA
s. y
A
kA
kB
k
Sendero de crecimiento:
El crecimiento de la productividad
resulta de incrementos de la
cantidad de capital que cada
trabajador debe operar⇒ ∆y=f(k).
No obstante, a medida que k aumenta
la productividad del capital declina.
El trabajo es el factor limitante.
La economía de dirige hacia un estado
estacionario
El estado estacionario:
Se define el estado estacionario (punto BA)
como la posición de equilibrio de largo
plazo de la economía⇒ k=kB es una
solución estable en donde ∆k=0.
Las diferentes variables (L,K,Y) crecen a una
misma tasa:
∆Y/Y=∆K/K=∆L/L = n
La intensidad capitalística (k=K/L) no crece
más.
La productividad del trabajo (y=Y/L) no
crece más.
conclusión: el crecimiento sostenido
del producto per cápita en el largo
plazo depende de cómo va a ir
deprimiendo la acumulación del
capital su productividad marginal y
de si existen fuerzas que
contrarresten la tendencia declinante
de esa productividad.
Y/L constante
No se explica en la historia económica de la
época de crecimiento de los treinta gloriosos
El ingreso per cápita de los países desarrollados creció durante los
treinta gloriosos (1950-70)
Debraj Ray: la acumulación del capital no es
suficiente para que la renta per cápita crezca
continuamente
El progreso técnico exógeno
El progreso técnico es una fuerza exógena que
contrarresta la declinación de la productividad
marginal del capital.
Concepción del progreso técnico
• Se define el progreso técnico como una
deformación de la función de producción.
• El progreso técnico debe ser
necesariamente extra-económico
(exógeno): por el teorema de Euler, una
vez pagados el capital y el trabajo, no
quedan recursos para compensar la
actividad científica-tecnológica.
• El conocimiento tecnológico es un bien
libre o público, es decir es algo que está
accesible para todo el mundo de forma
gratuita.
Concepción del progreso
técnico exógeno
• Se define el progreso técnico como
una deformación de la función de
producción.
• Progreso Técnico potenciador del trabajo
Y=F(K,AL)
• El progreso técnico constituye un factor exógeno que
crece a un ritmo constante y es esencial para el
crecimiento económico a largo plazo. El progreso
técnico mejora la productividad del trabajo, impidiendo la
baja del producto marginal del capital cuando la razón
aumenta. Considerando que a largo plazo el crecimiento
de la tecnología nunca llega al límite, a un tope, como
tampoco la productividad del trabajo, por consiguiente,
la tasa de crecimiento del ingreso real per capita no
puede ser reducida a cero.
• Para el contexto de este modelo, el crecimiento
económico es durable, pero los factores que explican la
tasa de crecimiento de largo plazo son analizados y
tomados exógenamente (tasa de crecimiento de la
población, tasa de crecimiento del progreso técnico).
• Esta concepción del progreso técnico es relativamente
débil, dado que su naturaleza no es especificada, y su
ritmo determinado fuera de la esfera económica.
La dinámica de transición hacia la convergencia
económica
• El modelo de Solow predice que en el largo plazo los
productos per cápita de todos los países crecerán a la
misma tasa (t) determinada exógenamente. Ello es así
porque la tecnología es un bien público.
• La dinámica de transición: al ser las condiciones
iniciales diferentes de un país a otro (relación inicial
entre capital y trabajo), las economías crecerán a
diferentes tasas en sus procesos hacia el equilibrio de
largo plazo.
• En los países en donde el capital es el factor
relativamente más escaso (países pobres) se espera
que las tasas de crecimiento sean más elevadas.
• A la larga, las brechas en los niveles de ingreso per
cápita entre países ricos y pobres deberían desaparecer
(siempre y cuando n, s y d sean idénticas).
Qué políticas de crecimiento?
• La recomendación genérica que se deriva
de este modelo propugna prescindir de la
intervención estatal, políticas de
liberalización económica y de
desregulación.
De la hipótesis de convergencia se
deduce que no es necesario aplicar
políticas regionales específicas.
• CONVERGENCIA ABSOLUTA: Si todas las
economías tienen acceso a las mismas
tecnologías, tienen tasa de ahorro, de
depreciación y de crecimiento demográfico
similares, tendrán el mismo estado estacionario
y, en consecuencia, los países más pobres
crecerán más rapidamente.
• Siendo la tecnología un bien público, si todos
los países comparten tasas similares de ahorro,
de crecimiento demográfico y de depreciación,
todos ellos deberán converger al mismo estado
estacionario.
• La CONVERGENCIA ABSOLUTA significa que
la tasa de crecimiento será mayor cuanto menor
sea el nivel de renta per-cápita del país.
Evidencia empírica
Crec. Interanual de la Renta por hbt. 1960
1960-1998
Relación entre 60 países: ¿Convergencia
Absoluta?
9%
R2= 0.029
y = 0.0033Ln(x) + 0.0072
6%
3%
0%
0
20
40
60
80
100
120
-3%
Renta per-cápita en relación a la de Estados Unidos en 1960
Fuente: Elaboración a partir de las World Penn Tables –curso Pompeu
Convergencia Ex-post
Los que ahora son “ricos”
Desarrollados Hasta España (>53% de la renta per cápita de EEUU en 1998)
7%
SINGAPUR
2
y = -0.0218Ln(x)
+ 0.1176
R = 0.8701
6%
5%
4%
España
3%
2%
Suiza
1%
0%
0
20
40
60
80
100
120
¿Hay otro club que converge más lentamente?
De Grecia a Bolivia (entre 10% y 50% de la Renta per-capita de USA en 1998)
Corea
6%
5%
2
y = -0.0152Ln(x)
+ 0.0651
R = 0.3853
4%
3%
Argentina
2%
1%
0%
0.00
10.00
20.00
30.00
40.00
50.00
60.00
70.00
Los más pobres
De la India a Tanzania (Menos del 10% de la renta per cápita de USA)
4%
y = -0.015Ln(x) + 0.0357
R2 = 0.392
India
Lesotho
3%
2%
1%
¡
0%
0.00
-1%
-2%
-3%
5.00
10.00
15.00
20.00
Zambia
República Centroafric.
Mozambique
25.00
Nicaragua
30.00
• CONVERGENCIA RELATIVA: Si los
países tienen acceso a las mismas
tecnologías y distintos estados
estacionarios, sus diferencias sólo pueden
explicarse por diferencias en sus tasas de
ahorro, crecimiento demográfico o tasas
de depreciación