laboratorio de fÃ−sica. práctica: osciloscopio. introducción.

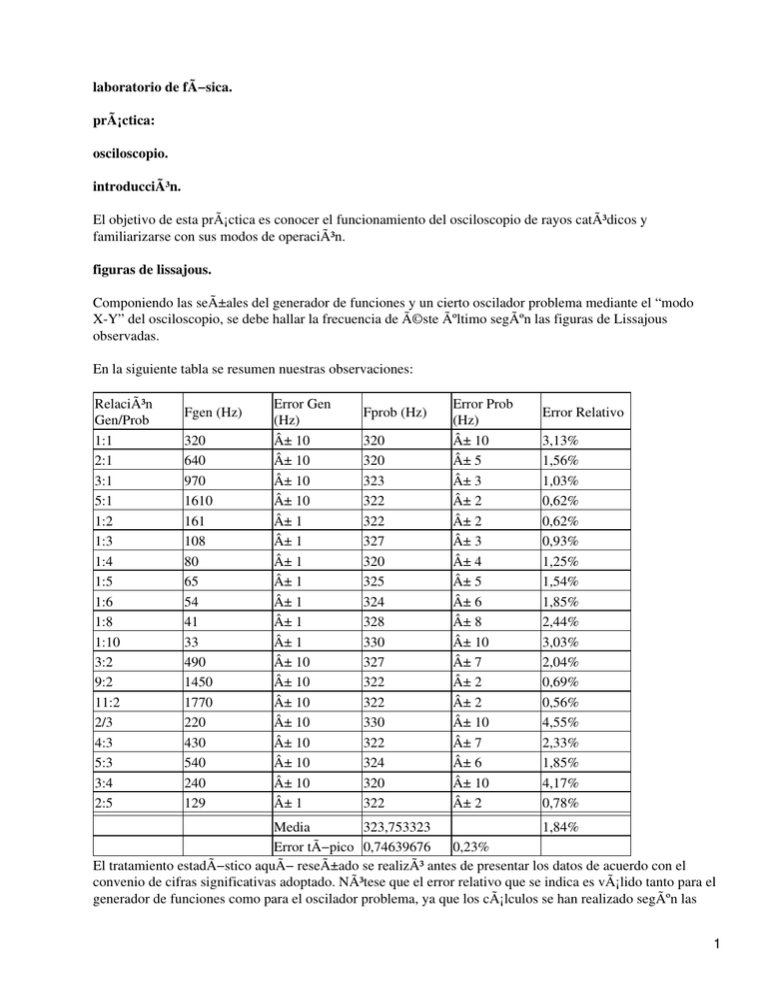
laboratorio de fÃ−sica.
práctica:
osciloscopio.
introducción.
El objetivo de esta práctica es conocer el funcionamiento del osciloscopio de rayos catódicos y
familiarizarse con sus modos de operación.
figuras de lissajous.
Componiendo las señales del generador de funciones y un cierto oscilador problema mediante el “modo
X-Y” del osciloscopio, se debe hallar la frecuencia de éste último según las figuras de Lissajous
observadas.
En la siguiente tabla se resumen nuestras observaciones:
Relación
Gen/Prob
1:1
2:1
3:1
5:1
1:2
1:3
1:4
1:5
1:6
1:8
1:10
3:2
9:2
11:2
2/3
4:3
5:3
3:4
2:5
Fgen (Hz)
320
640
970
1610
161
108
80
65
54
41
33
490
1450
1770
220
430
540
240
129
Error Gen
(Hz)
± 10
± 10
± 10
± 10
± 1
± 1
± 1
± 1
± 1
± 1
± 1
± 10
± 10
± 10
± 10
± 10
± 10
± 10
± 1
Fprob (Hz)
320
320
323
322
322
327
320
325
324
328
330
327
322
322
330
322
324
320
322
Error Prob
(Hz)
± 10
± 5
± 3
± 2
± 2
± 3
± 4
± 5
± 6
± 8
± 10
± 7
± 2
± 2
± 10
± 7
± 6
± 10
± 2
Error Relativo
3,13%
1,56%
1,03%
0,62%
0,62%
0,93%
1,25%
1,54%
1,85%
2,44%
3,03%
2,04%
0,69%
0,56%
4,55%
2,33%
1,85%
4,17%
0,78%
Media
323,753323
1,84%
Error tÃ−pico 0,74639676
0,23%
El tratamiento estadÃ−stico aquÃ− reseñado se realizó antes de presentar los datos de acuerdo con el
convenio de cifras significativas adoptado. Nótese que el error relativo que se indica es válido tanto para el
generador de funciones como para el oscilador problema, ya que los cálculos se han realizado según las
1
fórmulas
y
En resumen, para el oscilador problema hemos determinado
Método de la elipse.
Componiendo esta vez la señal del generador de funciones con otra desfasada mediante un circuito
capacitivo, determinaremos el valor de dicho desfase mediante el método descrito en el manual.
Nuestras observaciones se resumen a continuación:
Medidas
Valores
Errores
AB,
Error Ï
Error
CD Amplitud(V) sen Ï
Ï (rad)
Error sen Ï
(rad)
relativo Ï
(V)
Eje X
5,6 7,2
0,77777778 0,891122508 0,12345679 0,19641855 0,220417
Eje Y
8,8 12
0,73333333 0,823211977 0,072222222 0,10622957 0,12904279
<Ï >
0,857167243
0,03395527 0,03961335
Método
<sen Ï >
0,75555556 0,856501772 0,022222222 0,03392268 0,03960608
Según el método empleado en cada caso utilizamos propagación de errores o cálculo estadÃ−stico,
pero se observa que en ambos casos obtenemos unos valores finales muy similares:
Diodo.
Mediante distintas pruebas en distintos modos de funcionamiento del osciloscopio se estudiará un diodo y su
curva caracterÃ−stica.
Identificando en cada caso, hallamos:
Método
Curva CaracterÃ−stica
V0 (V)
VR0 (V)
VC (V)
1,5 ± 0,1
0,9 ± 0,1
0,4 ± 0,1
R= 10 kï”
Curva CaracterÃ−stica
1,5 ± 0,1
1,0 ± 0,1
0,5 ± 0,1
R= 1 kï”
Señales de entrada y
1,5 ± 0,1
1,0 ± 0,1
0,5 ± 0,1
salida
Se observa que para los tres casos el resultado es prácticamente igual.
Aumentamos la frecuencia manteniendo la amplitud, y hallamos los siguientes puntos en los que aparecÃ−a
una cierta corriente en sentido inverso:
Señal temporal: fC= 1000 ± 20 Hz
Curva caracterÃ−stica: fC= 950 ± 20 Hz
2
Al conectar el puente de diodos obtuvimos una señal rectificada en onda completa, esto es, los
semiperÃ−odos negativos, en vez de ser eliminados, son invertidos, de forma que lo que se obtiene a la salida
del puente de diodos es aproximadamente la señal senoidal en valor absoluto.
F= (323,8 ± 0,7) Hz (± 0,23%)
Ï = 0,85 ± 0,03 rad (± 3,4 %)
3