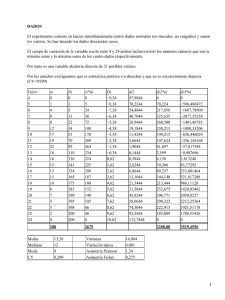
MODULO 06 *.

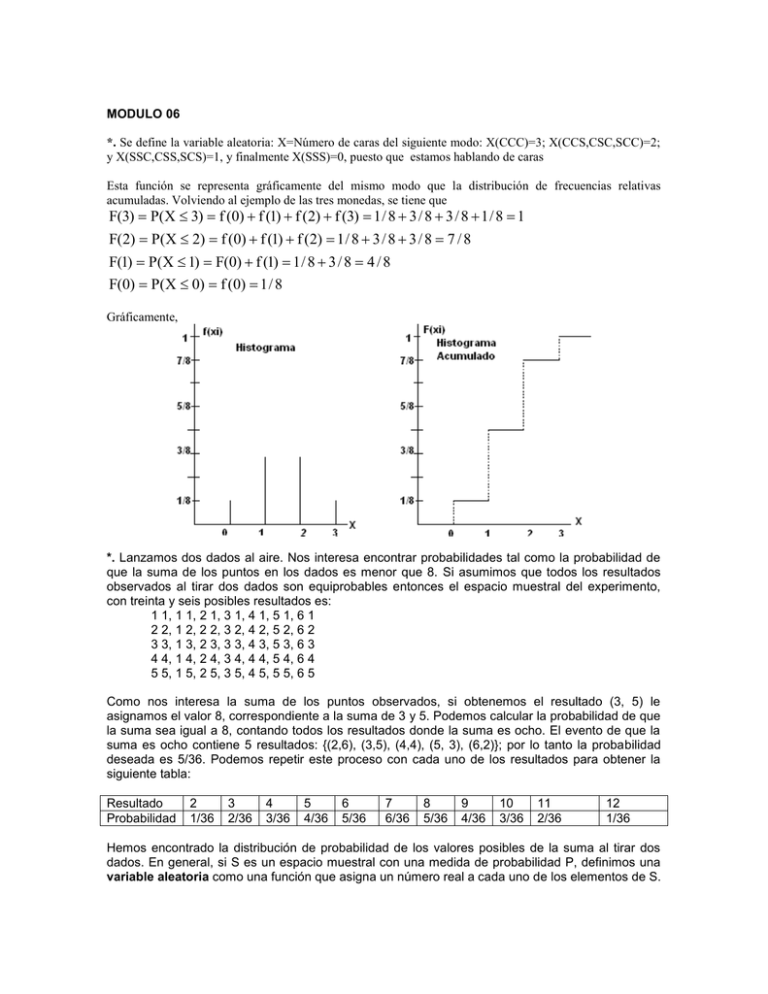
MODULO 06
*. Se define la variable aleatoria: X=Número de caras del siguiente modo: X(CCC)=3; X(CCS,CSC,SCC)=2;
y X(SSC,CSS,SCS)=1, y finalmente X(SSS)=0, puesto que estamos hablando de caras
Esta función se representa gráficamente del mismo modo que la distribución de frecuencias relativas
acumuladas. Volviendo al ejemplo de las tres monedas, se tiene que
F(3)  P(X  3)  f (0)  f (1)  f (2)  f (3)  1 / 8  3 / 8  3 / 8  1 / 8  1
F(2)  P(X  2)  f (0)  f (1)  f (2)  1 / 8  3 / 8  3 / 8  7 / 8
F(1)  P(X  1)  F(0)  f (1)  1 / 8  3 / 8  4 / 8
F(0)  P(X  0)  f (0)  1 / 8
Gráficamente,
*. Lanzamos dos dados al aire. Nos interesa encontrar probabilidades tal como la probabilidad de
que la suma de los puntos en los dados es menor que 8. Si asumimos que todos los resultados
observados al tirar dos dados son equiprobables entonces el espacio muestral del experimento,
con treinta y seis posibles resultados es:
1 1, 1 1, 2 1, 3 1, 4 1, 5 1, 6 1
2 2, 1 2, 2 2, 3 2, 4 2, 5 2, 6 2
3 3, 1 3, 2 3, 3 3, 4 3, 5 3, 6 3
4 4, 1 4, 2 4, 3 4, 4 4, 5 4, 6 4
5 5, 1 5, 2 5, 3 5, 4 5, 5 5, 6 5
Como nos interesa la suma de los puntos observados, si obtenemos el resultado (3, 5) le
asignamos el valor 8, correspondiente a la suma de 3 y 5. Podemos calcular la probabilidad de que
la suma sea igual a 8, contando todos los resultados donde la suma es ocho. El evento de que la
suma es ocho contiene 5 resultados: {(2,6), (3,5), (4,4), (5, 3), (6,2)}; por lo tanto la probabilidad
deseada es 5/36. Podemos repetir este proceso con cada uno de los resultados para obtener la
siguiente tabla:
Resultado
Probabilidad
2
1/36
3
2/36
4
3/36
5
4/36
6
5/36
7
6/36
8
5/36
9
4/36
10
3/36
11
2/36
12
1/36
Hemos encontrado la distribución de probabilidad de los valores posibles de la suma al tirar dos
dados. En general, si S es un espacio muestral con una medida de probabilidad P, definimos una
variable aleatoria como una función que asigna un número real a cada uno de los elementos de S.
Es decir X es una función cuyo dominio es el espacio muestral S y su codominio es el conjunto de
números reales
Interpretamos, por ejemplo X = 8 como el evento de que se observó el resultado 8 al tirar los dos
dados, es decir el evento { (2,6), (3,5), (4,4), (5, 3), (6,2)} ocurrió. También asignamos a X = 8 la
probabilidad de ese evento. Así vemos que P( X = 8 ) = P({ (2,6), (3,5), (4,4), (5, 3), (6,2)}) = 5/36.
Nota que a pesar de que X es una función, usualmente no se escribe el argumento de la función,
es decir, si s es un elemento del espacio muestral S, en vez de escribir X(s), sencillamente
escribimos X. Es usual denotar las variables aleatorias por letras mayúsculas y los valores que
puede asumir por letras minúsculas.
Para el ejemplo de la suma de los puntos al tirar dos dados, los valores de esta función están
dados en la Tabla, la cual se puede reescribir usando los conceptos estudiados.
x
2
3
4
5
6
7
8
9
10
11
12
f( x)
1/36
2/36
3/36
4/36
5/36
6/36
5/36
4/36
3/36
2/36
1/36
La probabilidad de observar un valor particular de la variable aleatoria, digamos X = 3 está dado
por la altura de la barra sobre el 3, es decir P(X = 3) = 2/36. De igual manera, en vez de asociar la
altura de la barra con la probabilidad, podemos ver que el área de la barra sobre el 3 es 2/36 1 =
2/36, ya que la altura de la barra es 2/36 y su ancho es 1. Usar el área de las barras para
representar la probabilidad es muy útil para extender la noción de probabilidad a otras variables.
Podemos usar el histograma de probabilidad para calcular probabilidades tal como P( X 4).
Vemos que P(X 4) = P(X =2 ó X =3 ó X =4) = P(X = 2) + P(X = 3) + P(X = 4) , ya que los eventos
donde X = 2, X= 3 y X=4 son disjuntos. Entonces P( X 4) = 1/36 + 2/36 + 3/36 = 6/36, sumando
las áreas de la barras que están sobre el 4 y a su izquierda. Debemos ser muy cuidadosos con las
desigualdades, ya que P( X 4) = 6/36, mientras que P( X< 4) = 3/26.
*. En el Lanzamiento de una Moneda, X: Número de Sellos
*. X es la Suma Obtenida en el Lanzamiento de dos Dados:
*. Si X: Diferencia en Valor Absoluto, entre los dos Sectores de una Ficha de Dominó:
*. Cálculo de probabilidades para el lanzamiento del par de dados, donde X es la suma obtenida:
Consultando directamente en la función de distribución de esta variable discreta, F(x)=p(X≤x)
tenemos:
Cálculo de probabilidades: supongamos que un practicante de tiro al blanco siempre acierta
indistintamente, en un círculo de 20 centímetros de radio.
La distancia que hay entre el punto “a=0” (centro) y cualquier punto de la circunferencia “b=20” es
20-0.
Entonces,
¿ Cuál es la probabilidad que un disparo impacte a menos de 15 cm del centro? ¿ a más de 9
centímetros? ¿Entre 7 y 14 centímetros?
*. Para fichas de dominó, si X representa la diferencia absoluta entre los dos números, representar
y calcular la probabilidad de ocurrencia de los siguientes eventos:
a La diferencia sea menor o igual a 5
b La diferencia sea mayor que 2
c La diferencia sea mayor que 2 pero menor o igual 5
d La diferencia sea mayor que 5 ó menor que 3
Ejemplo, Consideramos una variable aleatoria discreta con función de probabilidad:
Obtener:
1. El valor de la constante c para que sea una función de probabilidad.
2. Los valores de las funciones de probabilidad y distribución para
3. Calcular
Solución:
y
.
1.
ya que tenemos la suma de una progresión geométrica de razón menor que la unidad:
Luego c=3. Así la función de probabilidad es:
Ejemplo, Calculemos sucesivos valores de f(x) y F(x):
xi
f(x)
F(x)
2
3/4=0,75
0,75
3
3/16=0,19
0,94
4
3/64=0,047 0,987
5
3/256=0,012 0,999
Se observa que cuando
,
y
Ejemplo, Consideremos una variable aleatoria continua con función de densidad
Se pide:
1. El valor de la constante c para que sea una función de densidad.
2. La función de distribución.
3. La media o valor esperado.
4. Probabilidad de que la variable este comprendida entre 0,2 y 0,7
Solución:
1.
Por ser f una densidad se ha de verificar:
2.
Luego, la función de distinción es
3. Media :
4.
Ejemplo, La variable aleatoria continua X tiene como función de densidad:
Determinar :
1. Media
2. Varianza
3.
Solución:
1.
2.
1 ya
ha
2es:
Luego
3. Hay que calcular la probabilidad del intervalo de la Figura:
Ejercicio, Se desarrolla un compuesto para aliviar las migrañas. El fabricante afirma que es efectivo en un
90% de los casos. Se prueba sobre 4 pacientes. Sea X el número de pacientes que obtiene alivio.
a. Encontrar la fdp para X, suponiendo que la afirmación del fabricante sea correcta.
b. Encontrar p(X1)
c. Si el compuesto no alivia a ninguno de los pacientes ¿es esa una razón para poner en duda la eficacia
afirmada por el fabricante? Razonar sobre la base de la probabilidad implicada.
d. Calcular la media. ¿Qué significa en este ejemplo?
Solución. a. Representando por a que un paciente tenga alivio y por n que no lo tenga, el espacio muestral
para el problema es  = {aaaa, naaa, anaa, aana, aaan, ..., nnnn}, Si es cierta la afirmación del fabricante
p(a)=0,9 y p(n)=0,1. La v.a. X: número de pacientes que tienen alivio puede tomar los valores 0, 1, 2, 3, 4. La
tabla con la fdp inducida es
X
Sucesos
f(x)
0
{nnnn}
0,14
1
{annn, nann, nnan, nnna}
4x0,9x0,13
2
{aann, anan, anna, naan, nana, nnaa }
6x0,92x0,12
3
{aaan, aana, anaa, naaa}
4x0,93x0,1
4
{aaaa}
0,94
4
3
b. p(X1) = f(0) + f(1) = 0,1 + 4x0,9x0,1 = 0,0037
c. La probabilidad de que no alivie a ningún paciente es f(0)=0,0001. Es una probabilidad tan baja que,
efectivamente, si ese fuera el resultado hay suficientes razones para poner en duda la afirmación de que alivia
al 90% de los pacientes.
d.
Si se repitiera un número suficientemente grande de veces la experiencia de administrar el fármaco a 4
pacientes, el número promedio de pacientes que experimentarían alivio sería 3,6.
Ejercicio, Sea X el tiempo de supervivencia en años después de un diagnóstico de leucemia aguda. La fdp
para X es f(x) = -x/2 + 1, para 0 < x < 2.
a. Comprobar que es una fdp.
b. Hallar p(X>1)
c. Hallar p(X=1)
d. Hallar p(X1)
Ayuda: hacerlo todo gráficamente
e. Calcular la media y la varianza (Sólo para iniciados).
Solución
a. La gráfica de la fdp es
La condición equivalente a
para variables continuas es que el área bajo la fdp sea 1. De modo general ese área se calcula mediante cálculo
integral, pero en este caso se puede calcular por la conocida fórmula del área de un triángulo A = (bxh)/2, es
decir A = (2x1)/2=1
b.
Gráficamente, la probabilidad pedida es el área coloreada de verde, por lo tanto se puede calcular
también con la fórmula del área del triángulo. Ahora b=1 y para calcular h hay que ver que valor
toma la fdp cuando x=1, y = -1/2 + 1 = 1/2. Por lo tanto, la probabilidad es (1x1/2)/2 = ¼
c. Como en toda variable continua la probabilidad de que tome un valor concreto es 0, por lo tanto
p(X=1) = 0
d. Obviamente p(X 1) = p(X >1) = ¼
e. Media
varianza