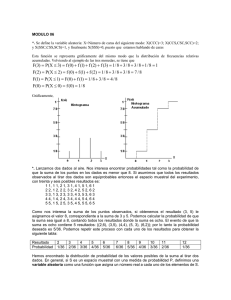
05 – Funciones de densidad de probabilidad
Anuncio

05 – Funciones de densidad de probabilidad Diego Andrés Alvarez Marín Profesor Asistente Universidad Nacional de Colombia Sede Manizales 1 Contenido ● FDP uniforme ● FDP beta ● FDP exponencial ● FDP normal ● FDP gamma 2 Sobre la selección de las FMPs/FDPs La elección de una FMP/FDP para representar un fenómeno de interés práctico debe estar motivada tanto por la compresión de la naturaleza del fenómeno en sí, como por la posible verificación de la FMP/FDP seleccionada a través de la evidencia empírica. 3 FDP Uniforme ~U(a,b) La variable aleatoria toma valores sobre un intervalo de manera que la medida de probabilidad se encuentra uniformemente distribuída sobre ese intervalo. Esto es, la probabilidad que la variable aleatoria tome un valor en cada subintervalo de igual longitud es la misma. 4 FDP Uniforme ~U(a,b) Momentos de la FDP: Ejemplo: redondeo del peso de una persona: 67 kg significa un peso entre 66.5 kg y 67.5 kg El error de redondeo se encuentra distribuído uniformemente en el rango [-0.5kg, 0.5 kg] 5 FDP Uniforme ~U(a,b) 6 Principio de indiferencia de Laplace http://en.wikipedia.org/wiki/Principle_of_indifferen ce ● La dirección según la cual las ondas producidas por un terremoto pueden aproximarse a una estructura pueden considerarse en ausencia de información en contra, que se distribuye ○ ○ uniformemente en el intervalo [0 , 360 ). 7 FDP Uniforme en MATLAB 8 FDP Beta ~ B(α,β) Se utiliza para representar variables físicas cuyos valores se encuentran restringidos a un intervalo de longitud finita ej: distribución de artículos defectuosos sobre un intervalo de tiempo. Como es una FDP muy flexible, generalmente se utiliza para la descripción empírica de datos 9 FDP Beta ~ B(α,β) 10 11 12 La FDA Beta ~ B(α,β) 13 La FDA Beta ~ B(α,β) 14 FDP Beta en MATLAB y MS EXCEL 15 FDP Exponencial Con la FDP exponencial se modela el lapso de tiempo entre dos eventos consecutivos de Poisson que ocurren de manera independiente y a una frecuencia constante. Ejemplo: intervalo de tiempo entre los arribos de vehículos a un punto. 16