97 - IES Los Pedroches
Anuncio

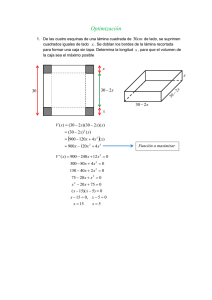
I.E.S. Los Pedroches. 2º de Bachillerato - Matemáticas II de las CC.SS. Curso 2003-04. EJERCICIO 1 DE SELECTIVIDAD Sep’97 A Cada mes una empresa puede gastar, como máximo 1000000 pta en salarios y 1800000 pta en energía (electricidad y gasoil). La empresa sólo elabora dos tipos de productos A y B. Por cada unidad de A que elabora gana 80 pta y 50 pta por cada unidad B. El coste salarial y energético que acarrea la elaboración de una unidad del producto A y una del B aparece en la siguiente tabla: A B Coste salarial 200 100 Coste energético 100 300 Se desea determinar cuántas unidades de cada uno de los productos A y B debe producir la empresa para que el beneficio sea máximo. Producto A Producto B Total Coste salarial en ptas/u Coste energético en ptas/u Beneficio en ptas/u 200 100 80 100 300 50 # 1.000.000 # 1.800.000 Nº de unidades x y Beneficio: z 80 x 50 y (ha de ser máximo). Restricciones: 200 x 100 y # 1.000.000 Y 2x y # 10.000 100 x 300 y # 1.800.000 Y x 3y # 18.000 x $ 0 ; y $ 0 (el número de unidades es no negativo) Región factible. Rectas: r1 / y 10.000 2x Y 18.000 x Y 3 x $ 0 Y r3 / x 0 r2 / y x y x y 0 5.000 10.000 0 18.000 3.000 0 5.000 y $ 0 Y r4 / y 0 Semiplanos: < P1 (0 , 0) Y 2 · 0 0 # 10.000 (V) Y P1 0 S1 (semiplano por debajo de r1 , incluida r1) 2x y # 10.000 /00 < P2 (0 , 0) Y 0 3 · 0 # 18.000 (V) Y P2 0 S2 (semiplano por debajo de r2 , incluida r2) x 3y # 18.000 /00 < x $ 0 e y $0 Y primer cuadrante incluidos los ejes . La región factible es la zona poligonal ABCD, incluidos los lados. Maximización. Vector director de la recta d / 80x 50y 0 Y vP (50 , 80) . (5.000 , 8.000) . El máximo se obtiene desplazando d paralelamente a sí misma dentro de la región factible: - el óptimo máximo se alcanza en C, punto de dicha región más alejado hacia la derecha. y 10.000 2x 18.000 x Y 10.000 2x Y x 2400 / C r1 _ r2 Y y 18.000 x 00 3 00 Y y 5200 Y C (2400, 5200) 3 0 Luego, se han de producir 2400 unidades de A y 5200 unidades de B. El máximo beneficio es: zmáx 80 · 2400 50 · 5200 452.000 ptas .