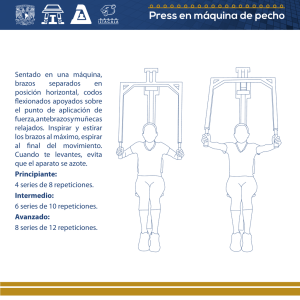
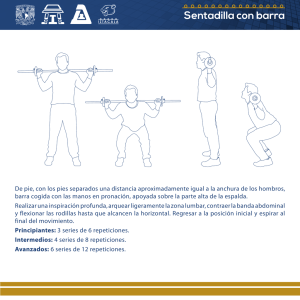
Series de Tiempo
Anuncio

Series de Tiempo Una serie de tiempo es una secuencia de datos puntuales medidos en tiempos sucesivos a intervalos de tiempo uniformes. La caracterización de las propiedades de una serie de tiempo se puede obtener mediante un modelo matemático que represente las variaciones observadas en los datos. Estos modelos proporcionan una representación compacta de las características de los datos en términos de unos cuantos parámetros (análogo al ajuste de distribuciones paramétricas de probabilidad). Los métodos de series de tiempo son adecuados cuando el orden de los datos en el tiempo es importante para una aplicación dada. Las observaciones atmosféricas separadas por períodos de tiempo relativamente cortos tienden a ser similares o a estar correlacionadas. Analizar y caracterizar la naturaleza de esas relaciones a lo largo del tiempo es útil para entender los procesos atmosféricos y para pronosticar eventos futuros. Es necesario tomar en cuenta esas correlaciones para hacer inferencias estadísticas válidas. Estacionariedad Estacionariedad.- Con frecuencia es razonable asumir que los valores pasados y futuros de una serie de tiempo son estadísticamente similares. La estacionariedad implica que la media y la función de autocovarianza de la serie de datos no cambian con el tiempo. • Cualitativamente, porciones diferentes de una serie de tiempo estacionaria son estadísticamente parecidas, aún cuando los valores individuales pueden ser muy diferentes. • Asumiendo estacionariedad, las propiedades estadísticas implícitas en el modelo (o proceso teórico) pueden usarse para inferir las carácterísticas de los valores aún no observados de la serie. • La mayoría de los métodos para el análisis de series de tiempo suponen estacionariedad en los datos. Sin embargo, muchos procesos atmosféricos no son estacionarios, p.e., datos que exhiben ciclos diurnos o anuales como la temperatura o el viento. • Existen dos formas para tratar con series no-estacionarias. Ambas incluyen el procesamiento de los datos de modo que permitan suponer estacionariedad de manera razonable. • Primera: Transformación matemática de los datos no-estacionarios para aproximar la estacionariedad. P.ej., restar una función periódica a los datos que están sujetos a un ciclo anual producirá una serie de datos transformados con media constante (cero). Para producir una serie que tenga media y varianza constantes, se pueden estandarizar las anomalías. Los datos que se vuelven estacionarios después de quitarles el ciclo anual se dice que exhiben cicloestacionariedad. • Segunda: Dividir los datos para realizar análisis separados sobre subconjuntos que sean suficientemente cortos para ser considerados como cercanamente estacionarios. Existen dos aproximaciones fundamentales para el análisis de series de tiempo: 1) en el dominio del tiempo, 2) en el dominio de la frecuencia. Son métodos complementarios que están ligados matemáticamente. • Métodos en el dominio del tiempo: Buscan caracterizar las series de datos en los mismos términos en los que son observados y reportados. Una herramienta primordial para la caracterización de las relaciones entre los datos en la aproximación del dominio del tiempo es la función de autocorrelación. Dominio del tiempo Datos discretos - La clase más común de modelo, o proceso estocástico, usado para representar series de tiempo de variables discretas es conocido como cadena de Markov, que puede considerarse como una colección de estados de un sistema. Datos continuos – Para la representación de la estructura de series de tiempo de variables continuas se utilizan modelos conocidos como modelos Box-Jenkins. El más simple es el modelo de autoregresión de primer orden, que es el análogo continuo de la cadena de Markov de primer orden para datos discretos. Autoregresión de primer orden (AR(1)) – Es una regresión lineal simple donde el predictando es el valor de la serie de tiempo al tiempo t + 1, xt+1, y el predictor es el valor actual de la serie de tiempo, xt. El modelo AR(1) puede escribirse como sigue: La serie de tiempo de x se supone estacionaria, de modo que su media μ es la misma para cada intervalo de tiempo. Las є's son cantidades aleatorias mutuamente independientes que tienen media μє = 0 y varianza σє2. Con frecuencia se asume además que siguen una distribución Gaussiana. El modelo AR(1) puede representar una correlación serial o persistencia de una serie de tiempo. Diagrama de dispersión de las temperaturas mínimas en Canandaigua durante Enero de 1987: los primeros 30 valores en el eje horizontal y del 2 al 31 en el eje vertical. El modelo AR(1) también puede interpretarse como un algoritmo para generar series de tiempo sintéticas de valores de x. Para valores positivos de ϕ, la serie de tiempo sintética exhibirá una correlación serial positiva ya que cada nuevo valor generado incluye alguna información del valor precedente. Este modelo comparte con la cadena de Markov de primer orden la propiedad de que la historia completa de la serie de tiempo anterior a xt no proporciona información adicional para xt+1, una vez que xt es conocido. AR(1) también es conocido como un proceso de ruido rojo, ya que un valor positivo del parámetro ϕ promedia o suaviza las fluctuaciones de corto plazo en la serie de valores independientes ε, mientras que afecta mucho menos las variaciones aleatorias más lentas o de baja frecuencia. Estimación de los parámetros del modelo autoregresivo de primer orden: μ es simplemente el promedio muestral del conjunto de datos y ϕ es igual al coeficiente de autocorrelación con retraso 1 ( ). Para que se cumpla la estacionariedad se requiere que -1 < ϕ < 1. Para la mayoría de las series de tiempo atmosféricas ϕ será positivo, lo cual refleja la persistencia. Valores negativos de ϕ corresponden a series de tiempo con valores alternados por encima y por debajo de la media o anticorrelacionados. La función de autocorrelación para una serie de tiempo gobernada por un proceso AR(1) puede escribirse en términos del parámetro autoregresivo como La varianza residual es también conocida como la varianza de ruido blanco y expresa la variabilidad o incertidumbre en la serie de tiempo que no es explicada por la correlación serial. Una forma de estimarla es mediante Proceso estocástico o aleatorio es lo contrario a un proceso determinístico. En lugar de tratar con una sola forma posible en la que el proceso pueda evolucionar en el tiempo, en un proceso estocástico hay alguna indeterminación descrita por distribuciones de probabilidad. Esto significa que aún si la condición inicial es conocida, existen muchas posibilidades hacia donde pueda ir el proceso, pero algunas trayectorias pueden ser más probales que otras. Modelos autoregresivos de orden K, AR(K) Dominio de la frecuencia – Análisis armónico • El análisis en el dominio de la frecuencia involucra la representación de series de datos en términos de contribuciones hechas en diferentes escalas de tiempo. • Una serie de tiempo de temperaturas horarias generalmente presenta variaciones en la escala de tiempo diaria (ciclo diurno del calentamiento solar) y en la escala de tiempo anual (paso de las estaciones). • En el dominio del tiempo, estos ciclos aparecerán como valores positivos grandes en la función de autocorrelación para retrasos de 24 horas y de 24x365 = 8760 horas. • En el dominio de la frecuencia tendremos contribuciones grandes a la variabilidad total de la serie de tiempo en períodos de 24 y 8760 horas, o en frecuencias de 1/24 = 0.0417 h-1 y 1/8760 = 0.000114 h-1. ● El análisis armónico consiste en la representación de las fluctuaciones en el tiempo mediante la suma de una serie de funciones seno y coseno. La suma de estas ondas reproduce los datos originales, pero son las intensidades relativas de las componentes individuales lo que más interesa. • Las funciones seno y coseno son armónicas en el sentido de que se escogen de modo que tengan frecuencias que son múltiplos enteros de la frecuencia fundamental determinada por el tamaño de la serie de tiempo. • Las funciones seno y coseno se calculan para ángulos positivos y negativos. Su patrón se repite cada 2π radianes o 360º. coseno seno radianes grados • Para cambiar de tiempo a frecuencia. Se considera la longitud de la serie de tiempo, n, como un ciclo completo o período fundamental. Como el ciclo completo corresponde a 360º o 2π radianes, se reescala proporcionalmente el tiempo a una medida angular usando: Frecuencia fundamental. Es una frecuencia angular que tiene dimensiones físicas de radianes por unidad de tiempo. Especifica la fracción del ciclo completo, que abarca n unidades en tiempo, que es ejecutada durante una unidad de tiempo. El subíndice 1 indica que pertenece a la onda que ejecuta un ciclo completo sobre toda la serie de datos. • Para representar las fluctuaciones en los datos. • C1 es la amplitud y es el ángulo fase. • La función tiene un máximo para Estimación de la amplitud y la fase de un armónico Similar a una regresión con dos predictores Es matemáticamente equivalente representar una onda armónica como una función coseno con amplitud C1 y fase ϕ1 o como la suma de dos funciones un coseno y un seno sin desplazamiento con amplitudes A1 y B1. En general, se puede usar el método de mínimos cuadrados para obtener el valor de los parámetros A1 y B1. Si nuestros datos están igualmente espaciados en el tiempo y no hay huecos en la serie, se pueden usar las siguientes relaciones: