Ejercicios de Gráficos Relleno de Pol´ıgonos
Anuncio
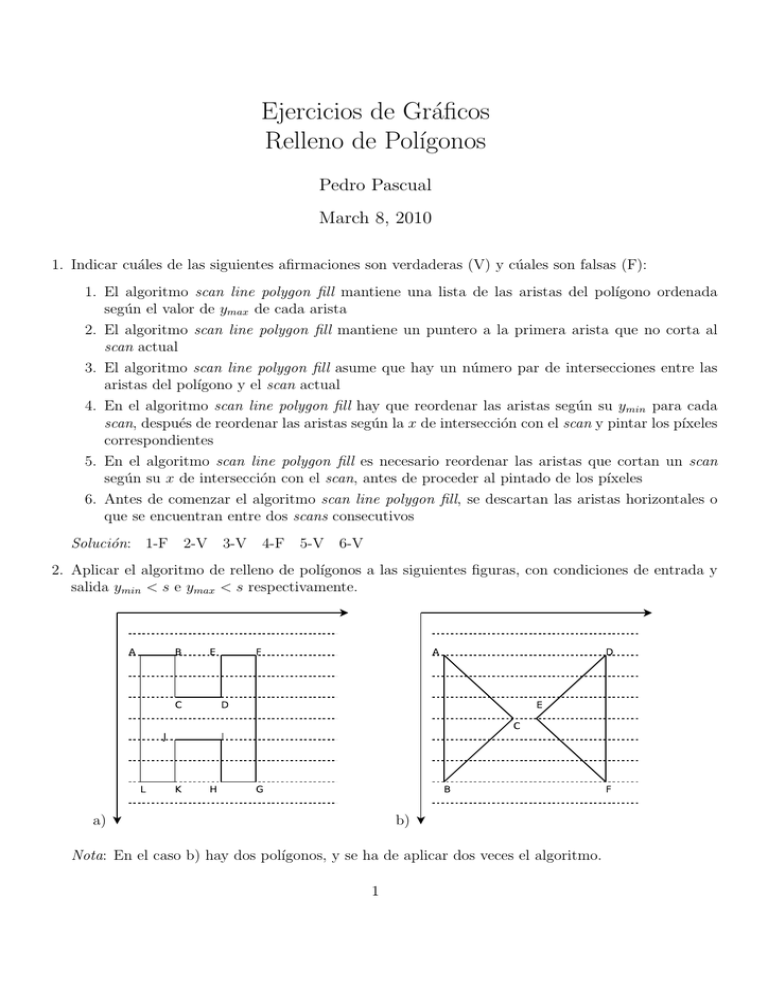
Ejercicios de Gráficos Relleno de Polı́gonos Pedro Pascual March 8, 2010 1. Indicar cuáles de las siguientes afirmaciones son verdaderas (V) y cúales son falsas (F): 1. El algoritmo scan line polygon fill mantiene una lista de las aristas del polı́gono ordenada según el valor de ymax de cada arista 2. El algoritmo scan line polygon fill mantiene un puntero a la primera arista que no corta al scan actual 3. El algoritmo scan line polygon fill asume que hay un número par de intersecciones entre las aristas del polı́gono y el scan actual 4. En el algoritmo scan line polygon fill hay que reordenar las aristas según su ymin para cada scan, después de reordenar las aristas según la x de intersección con el scan y pintar los pı́xeles correspondientes 5. En el algoritmo scan line polygon fill es necesario reordenar las aristas que cortan un scan según su x de intersección con el scan, antes de proceder al pintado de los pı́xeles 6. Antes de comenzar el algoritmo scan line polygon fill, se descartan las aristas horizontales o que se encuentran entre dos scans consecutivos Solución: 1-F 2-V 3-V 4-F 5-V 6-V 2. Aplicar el algoritmo de relleno de polı́gonos a las siguientes figuras, con condiciones de entrada y salida ymin < s e ymax < s respectivamente. b) a) Nota: En el caso b) hay dos polı́gonos, y se ha de aplicar dos veces el algoritmo. 1 March 8, 2010, Ejercicios de Gráficos-Relleno de Polı́gonos 2 3. Repetir el ejercicio anterior para las siguientes condiciones de entrada y salida: a) ymin ≤ s e ymax < s b) ymin ≤ s e ymax ≤ s c) ymin < s e ymax ≤ s 4. En el algoritmo de relleno de polı́gonos, ¿qué sucede en los siguientes casos?: a) ymin es un número entero. b) ymax es un número entero. c) ymin e ymax son distintos, pero tienen la misma parte entera. d) ymin e ymax son iguales, pero distintos de su parte entera. e) ymin e ymax son números enteros iguales. 5. Sea el polı́gono con vértices A = (10.5, 20.5), B = (30, 40) y C = (10.5, 59.5). Aplicar el algoritmo de relleno de polı́gonos con condiciones de entrada y salida ymin < s e ymax < s: a) Calcular para cada arista ymin , ymax , dx y el valor inicial de xint . b) Calcular smin y smax . c) Indicar cómo va progresando el algoritmo, con los cambios que hay en la lista de aristas y el puntero pout . No es preciso dar el valor de xint en cada scan, y basta indicar el rango de lı́neas en que la situación no cambia. Solución: arista ymin AB 20.5 BC 40 CA 20.5 ymax 40 59.5 59.5 dx 1 -1 0 xint 10 30 10.5 smin = 21, smax = 59 scan inicial 21 22 23 ... 39 40 41 42 ... 59 lista AB,CA,BC CA,AB,BC CA,AB,BC CA,AB,BC ... CA,AB,BC CA,AB,BC CA,BC CA,BC ... CA,BC xint pintado 10.5,11 10.5,12 10.5,13 ... 10.5,29 10.5,30 10.5,29 10.5,28 ... 10.5,11 11-11 11-12 11-13 ... 11-29 11-30 11-29 11-28 ... 11-11 Repetir el ejercicio para condiciones de entrada y salida ymin ≤ s e ymax ≤ s.