Autoevaluación 1. a) ¿A qué velocidad debe ser lanzada una bola
Anuncio
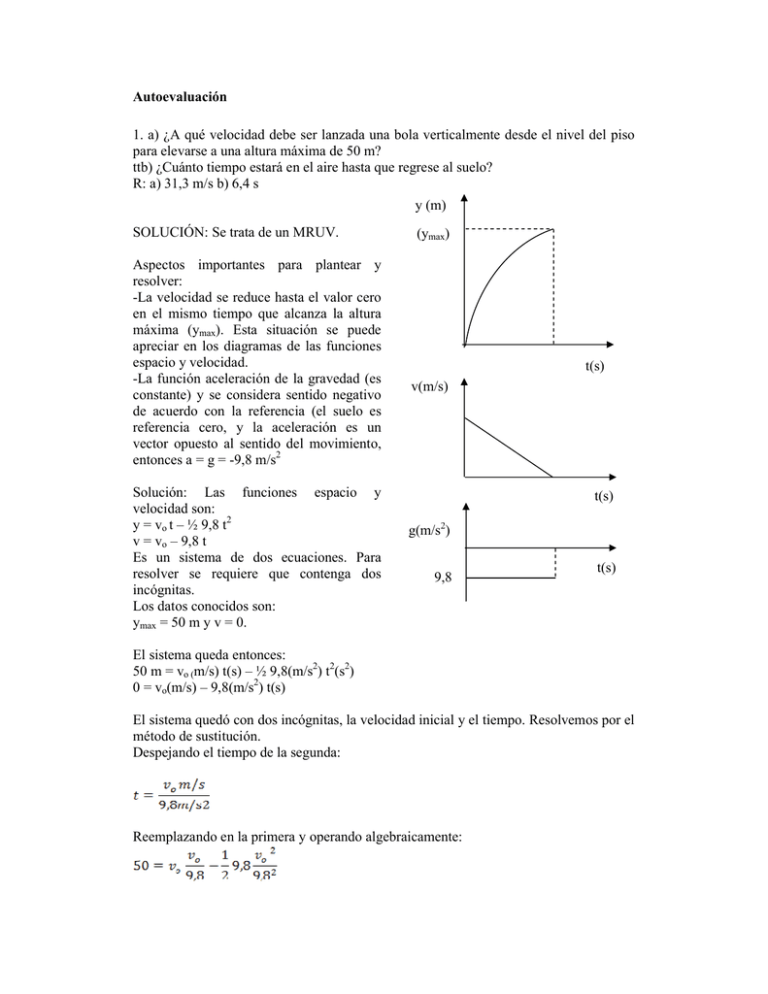
Autoevaluación 1. a) ¿A qué velocidad debe ser lanzada una bola verticalmente desde el nivel del piso para elevarse a una altura máxima de 50 m? ttb) ¿Cuánto tiempo estará en el aire hasta que regrese al suelo? R: a) 31,3 m/s b) 6,4 s y (m) SOLUCIÓN: Se trata de un MRUV. Aspectos importantes para plantear y resolver: -La velocidad se reduce hasta el valor cero en el mismo tiempo que alcanza la altura máxima (ymax). Esta situación se puede apreciar en los diagramas de las funciones espacio y velocidad. -La función aceleración de la gravedad (es constante) y se considera sentido negativo de acuerdo con la referencia (el suelo es referencia cero, y la aceleración es un vector opuesto al sentido del movimiento, entonces a = g = -9,8 m/s2 Solución: Las funciones espacio y velocidad son: y = vo t – ½ 9,8 t2 v = vo – 9,8 t Es un sistema de dos ecuaciones. Para resolver se requiere que contenga dos incógnitas. Los datos conocidos son: ymax = 50 m y v = 0. (ymax) t(s) v(m/s) t(s) g(m/s2) 9,8 t(s) El sistema queda entonces: 50 m = vo (m/s) t(s) – ½ 9,8(m/s2) t2(s2) 0 = vo(m/s) – 9,8(m/s2) t(s) El sistema quedó con dos incógnitas, la velocidad inicial y el tiempo. Resolvemos por el método de sustitución. Despejando el tiempo de la segunda: Reemplazando en la primera y operando algebraicamente: = 31,3 m/s Para calcular el tiempo, podemos utilizar las dos funciones. Si utilizamos la función velocidad, calcularemos el tiempo que demora en alcanzar la altura máxima, así: y para conocer el tiempo total hasta que regresa al suelo, se multiplica por dos: 2.3,2 s = 6,4 s Si utilizamos la función espacio, calcularemos el tiempo total igualando a cero la función (y = 0) de esta manera encontraremos el valor del tiempo en el momento de llegar al suelo, así: Despejando el tiempo (utilizamos la fórmula ) Vemos que la función cuadrática corta el eje x-x en dos puntos, uno es el origen y otro es un valor positivo. Esto nos anticipa que una raíz vale cero. Las raíces son: t1 = 0 s; t2 = 6,4 s 2. Un canguro es capaz de saltar hasta una altura de 2,62 m. Determine la velocidad de “despegue” del canguro. (velocidad inicial, al comienzo del salto). R. : 7,17 m/s SOLUCIÓN: Este ejercicio es similar al anterior, y se debe utilizar la misma herramienta matemática, por tratarse de un MRUV. Las funciones espacio y velocidad y los respectivos gráficos son igual. Datos: se conoce la altura máxima ymax = 2,62 m También es dato (si bien no se menciona) pero queda implícito, la velocidad al momento de altura máxima v = 0. y (m) (ymax) t(s) v(m/s) Las funciones espacio y velocidad forman un sistema de dos ecuaciones con dos incógnitas: vo y t. 2,62 m= vo (m/s) t(s) – ½ 9,8(m/s2) t2(s2) 0 = vo(m/s) – 9,8(m/s2) t(s) Despejamos el tiempo t de la segunda ecuación y reemplazando en la primera, luego de operar algebraicamente se obtiene la la fórmula Despejando t(s) g(m/s2) 9,8 t(s) (Se acepta el redondeo) 3. ¿Qué tan alto puede un humano tirar una pelota verticalmente hacia arriba si la velocidad inicial que puede imprimirle es de 40,23 m/s? R: 82,57 m SOLUCIÓN: Se trata de un MRUV. Las funciones espacio y velocidad forman un sistema de dos ecuaciones con dos incógnitas: Altura máxima (ymax) y el tiempo (t). y (m) = 40,23 (m/s) t(s) – ½ 9,8(m/s2) t2(s2) 0 = 40,23(m/s) – 9,8(m/s2) t(s) Despejamos el tiempo t de la segunda ecuación y reemplazando en la primera, luego de operar algebraicamente se obtiene la la fórmula 4. Se tira una pelota verticalmente hacia abajo con una velocidad inicial de 20,5 m/s desde una altura de 58,8 m. a) ¿Cuál será su velocidad justo antes de golpear contra el suelo? b) ¿Cuánto tiempo le lleva a la pelota llegar al suelo? R: a) 39,7 m/s b) 1,96 s y (m) SOLUCIÓN: Se trata de un MRUV. En este 58,8 caso la velocidad inicial tiene sentido hacia abajo, coincide con el sentido negativo de la aceleración “g” de la gravedad. Decimos que la velocidad aumenta con signo negativo. Las funciones espacio y velocidad forman un sistema de dos ecuaciones con dos incógnitas: velocidad de llegada (v(m/s) y el tiempo (t). 0=58,8 (m) -20,5 (m/s) t(s) – ½ 9,8(m/s2) t2(s2) v(m/s) = -20,5(m/s) – 9,8(m/s2) t(s) t(s) v(m/s) -20,5 Despejando el tiempo de la primera ecuación (utilizamos la fórmula ) podemos reemplazar en la segunda y resolvemos la velocidad. De acuerdo con el gráfico de la función cuadrática, obtendremos dos raíces: t1 = -24,5 s -39,12 t(s) 2 g(m/s ) 9,8 t2 = 1,9 s El valor que corresponde para el cálculo es t = 1,9 s Entonces la velocidad es: v = -20,5 m/s – 9,8 m/s2 1,9 s = -39,12 m/s t(s)