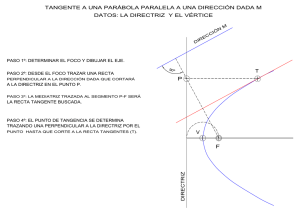
PARÁBOLA
Anuncio
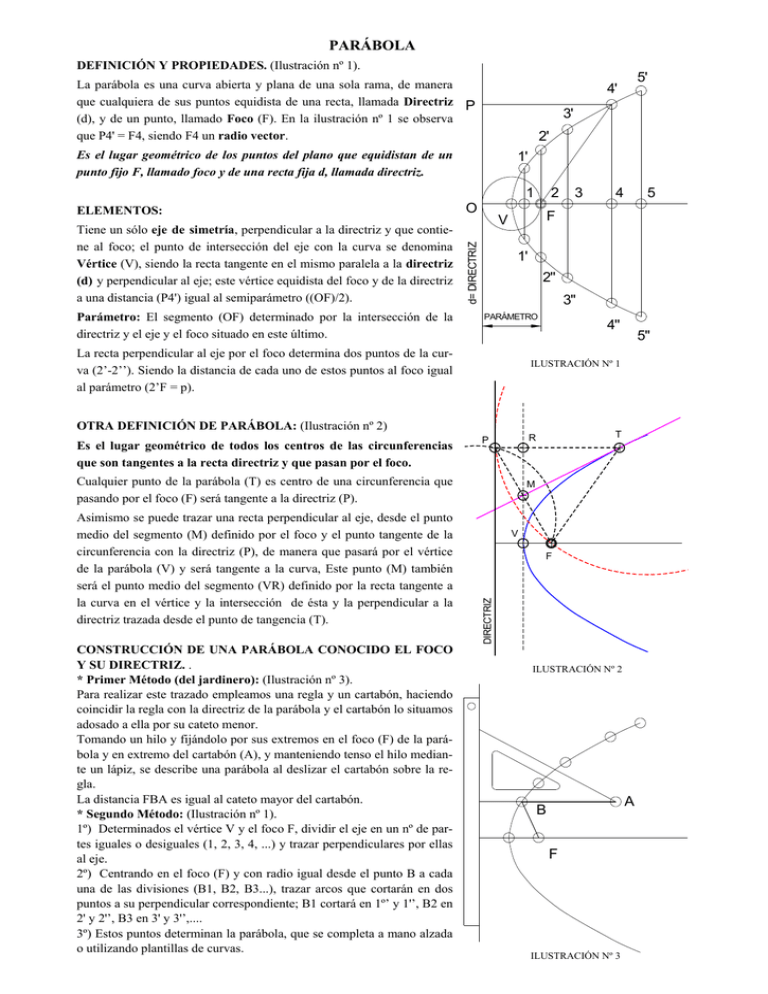
PARÁBOLA DEFINICIÓN Y PROPIEDADES. (Ilustración nº 1). La parábola es una curva abierta y plana de una sola rama, de manera que cualquiera de sus puntos equidista de una recta, llamada Directriz P (d), y de un punto, llamado Foco (F). En la ilustración nº 1 se observa que P4' = F4, siendo F4 un radio vector. 3' 2' Es el lugar geométrico de los puntos del plano que equidistan de un punto fijo F, llamado foco y de una recta fija d, llamada directriz. 1' ELEMENTOS: O Tiene un sólo eje de simetría, perpendicular a la directriz y que contiene al foco; el punto de intersección del eje con la curva se denomina Vértice (V), siendo la recta tangente en el mismo paralela a la directriz (d) y perpendicular al eje; este vértice equidista del foco y de la directriz a una distancia (P4') igual al semiparámetro ((OF)/2). d= DIRECTRIZ 1 Parámetro: El segmento (OF) determinado por la intersección de la directriz y el eje y el foco situado en este último. 4 5 1' 2'' 3'' PARÁMETRO 4'' 5'' ILUSTRACIÓN Nº 1 T R P Cualquier punto de la parábola (T) es centro de una circunferencia que pasando por el foco (F) será tangente a la directriz (P). M V F DIRECTRIZ CONSTRUCCIÓN DE UNA PARÁBOLA CONOCIDO EL FOCO Y SU DIRECTRIZ. . * Primer Método (del jardinero): (Ilustración nº 3). Para realizar este trazado empleamos una regla y un cartabón, haciendo coincidir la regla con la directriz de la parábola y el cartabón lo situamos adosado a ella por su cateto menor. Tomando un hilo y fijándolo por sus extremos en el foco (F) de la parábola y en extremo del cartabón (A), y manteniendo tenso el hilo mediante un lápiz, se describe una parábola al deslizar el cartabón sobre la regla. La distancia FBA es igual al cateto mayor del cartabón. * Segundo Método: (Ilustración nº 1). 1º) Determinados el vértice V y el foco F, dividir el eje en un nº de partes iguales o desiguales (1, 2, 3, 4, ...) y trazar perpendiculares por ellas al eje. 2º) Centrando en el foco (F) y con radio igual desde el punto B a cada una de las divisiones (B1, B2, B3...), trazar arcos que cortarán en dos puntos a su perpendicular correspondiente; B1 cortará en 1º’ y 1'’, B2 en 2' y 2'’, B3 en 3' y 3'’,.... 3º) Estos puntos determinan la parábola, que se completa a mano alzada o utilizando plantillas de curvas. 3 F OTRA DEFINICIÓN DE PARÁBOLA: (Ilustración nº 2) Asimismo se puede trazar una recta perpendicular al eje, desde el punto medio del segmento (M) definido por el foco y el punto tangente de la circunferencia con la directriz (P), de manera que pasará por el vértice de la parábola (V) y será tangente a la curva, Este punto (M) también será el punto medio del segmento (VR) definido por la recta tangente a la curva en el vértice y la intersección de ésta y la perpendicular a la directriz trazada desde el punto de tangencia (T). 2 V La recta perpendicular al eje por el foco determina dos puntos de la curva (2’-2’’). Siendo la distancia de cada uno de estos puntos al foco igual al parámetro (2’F = p). Es el lugar geométrico de todos los centros de las circunferencias que son tangentes a la recta directriz y que pasan por el foco. 5' 4' ILUSTRACIÓN Nº 2 A B F ILUSTRACIÓN Nº 3