Popiedades y Simplificación de Radicales
Anuncio
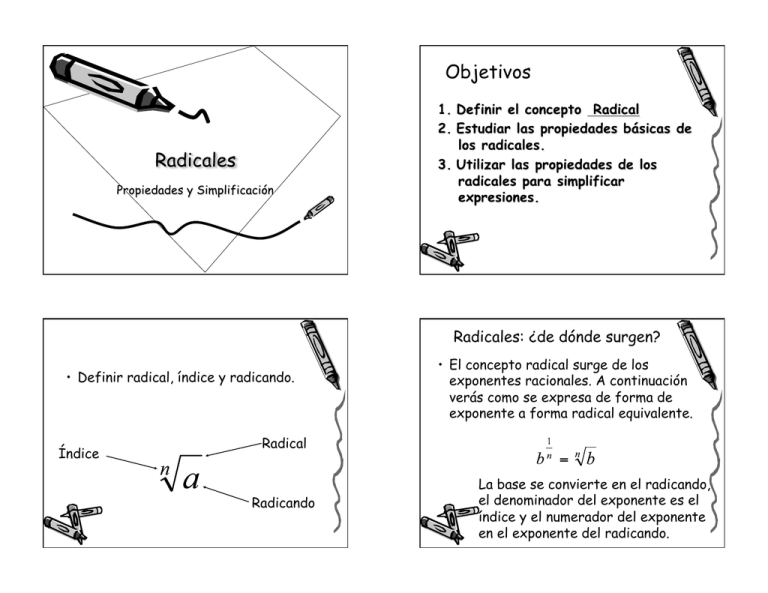
9/9 Objetivos Radicales: ¿de dónde surgen? • Definir radical, índice y radicando. Índice • El concepto radical surge de los exponentes racionales. A continuación verás como se expresa de forma de exponente a forma radical equivalente. Radical Radicando La base se convierte en el radicando, el denominador del exponente es el índice y el numerador del exponente en el exponente del radicando. 9/9 Ejemplos. Expresa en forma radical equivalente. Expresar en forma de exponentes. • Para expresar en forma de exponentes hacemos el proceso inverso: el radicando pasa a ser la base, el índice el denominador del exponente y el exponente de radicando el numerador del exponente. Nota: Cuando el índice es 2 no se escribe. Ejemplos: Expresa en forma de exponente racional. Propiedades 1) Ejemplos Si el índice y el exponente del radicando son iguales, podemos extraer la base. 2) Ejemplos Si tenemos un producto adentro de un radical, lo podemos separar como el producto de los radicales. 9/9 3) Ejemplos. Simplifica utilizando las propiedades. Ejemplos Un radical adentro de otro radical, multiplicamos los índices. 4) 1) = = Ejemplos Si el índice y el exponente del radicando tienen factor en común, los simplificamos. 5) Ejemplos = 2) 3) Un cociente adentro del radical, lo podemos separar como el cociente de dos radicales. = = = = = 4) 5) = 6) 7) = = = 9) = = = = 8) = = = = = = 10) = = = ¡Fin! 9/9 Ej. Propiedad #1 Ej. Propiedad #2 Si el índice y el exponente del radicando son iguales, podemos extraer la base. Si tenemos un producto adentro de un radical, lo podemos separar como el producto de los radicales. Regresar a Propiedades Ej. Propiedad #3 Regresar a propiedades Ej. Propiedad #4 Un radical adentro de otro radical, multiplicamos los índices. Regresar a propiedades Si el índice y el exponente del radicando tienen factor en común, los simplificamos. Regresar a propiedades 9/9 Ej. Propiedad #5 Un cociente adentro del radical, lo podemos separar como el cociente de dos radicales. Forma más simple de un radical 1. Ningún radicando (la expresión que está adentro del radical) contiene una potencia mayor o igual al índice. Viola condición 1 2. Ninguna potencia del radicando y el índice tienen factor común. Viola condición 2 3. No hay radicales en el denominador. Si el radical del denominador no simplifica, entonces RACIONALIZAMOS el denominador. ¿Qué es racionalizar? Viola condición 3 4. No hay fracción adentro del radical. Viola condición 4 Simplificación de Radicales La racionalización del denominador Al proceso de escribir una expresión racional con radicales en el denominador como otra expresión que no tiene radicales en el denominador se denomina como racionalizar el denominador. Aclaración: Para racionalizar el denominador de una expresión que tiene un solo término con raíz en el denominador, se multiplica el numerador y el denominador por una expresión con radical que eleve cada factor dentro del radicando a una potencia que coincida con el índice del radical. “De igual forma podemos racionalizar el numerador.” Racionalizar





