Planos de sombra
Anuncio
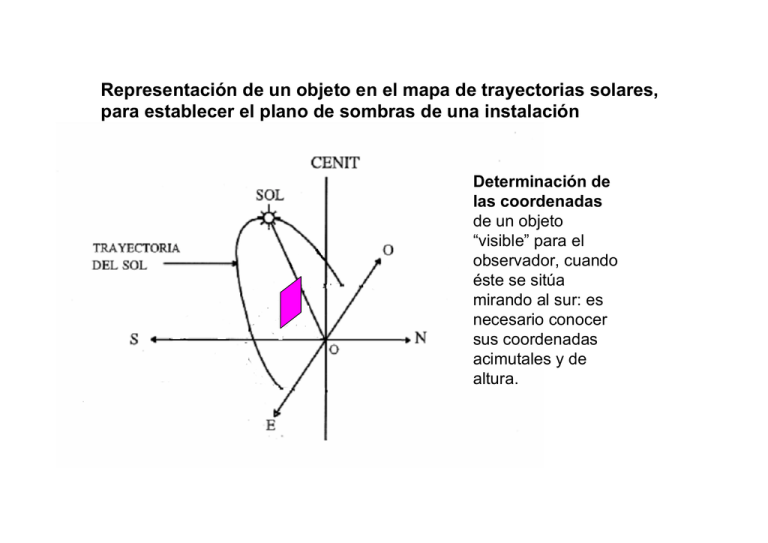
Representación de un objeto en el mapa de trayectorias solares, para establecer el plano de sombras de una instalación Determinación de las coordenadas de un objeto “visible” para el observador, cuando éste se sitúa mirando al sur: es necesario conocer sus coordenadas acimutales y de altura. Coordenadas x (eje del acimut) de un objeto en el mapa de las trayectorias solares a Objeto: b Línea a: delimita el “acimut” (izquierdo) del objeto para el observador. Es decir cuánto a la izq o derecha del S está el objeto respecto al observador. Línea b: delimita el acimut derecho. Estos ángulos son los que se utilizan en el mapa de las trayectorias solar en la coordenada x Vista aérea del objeto (plano horizontal) Cálculo de los ángulos acimutales del objeto: El ángulo Ψ a, definido por la línea a y el eje N-S, se calcula con x1 e y. El ángulo Ψ b definido por la línea b y el eje N-S se calcula con x2 e y. Cada ángulo es el arc tan(x/y) E Estos valores, Ψa y Ψb son los que se utilizan en el eje de la gráfica del plano de sombras (mapa de trayectorias solares) Observación: El cálculo de estos ángulos es trigonométrico. La utilización de signos negativos para la mañana para el ángulo acimutal (o al revés), es sólo un criterio (ver explicación en el pdf de ángulos posición relativa sol-tierra. Coordenadas y (eje de la altura solar en el mapa de las trayectorias solares d c Objeto: Línea c: define la altura del objeto en su parte izquierda, según lo ve el observador. La línea d define la altura del objeto en su parte derecha. Si el objeto está razonablemente alejado de la instalación, y su perfil es recto (no es un edificio que grande que tenga distintas alturas en su perfil frontal), se puede calcular uno sólo de estos valores (ya que son muy similares). Estos ángulos son los que se utilizan en el mapa de las trayectorias solar en la coordenada y Altura de un objeto, αr, en el mapa de las trayectorias solares (plano de sombras) Cénit del observador (línea perpendicular a su plano horizontal) O h S αr (x,y) r N E Para calcular el ángulo αr hay que utilizar h y r . r es la línea (verde) de la proyección de la línea que une el observador con el objeto (línea roja); es decir, se calcula como raiz_cuadrada de los valores x e y del objeto. El ángulo será arc tan(h/r). Donde h es la altura real del objeto. Este es el valor que hay que utilizar en el mapa de las trayectorias solares, en el eje y, el de la altura solar. Cuando se han “dibujado todos los objetos en el mapa de las trayectorias solares, se sombrea la zona “ocupada” por estos objetos. Si esta zona sombreada tiene zonas comunes con las líneas del mapa del plano de sombras (intersección), los objetos harán sombra en la instalación (ver figura inferior). Utilizando las tablas facilitadas se calcula, en función del porcentaje de área ocupada por el objeto, cuánta energía se perderá. Hay distintas tablas, para distintas inclinaciones del campo de paneles. 1 2 El objeto 1 produce sombras durante las dos primeras horas del día (las horas son las líneas “perpendiculares” que unen los distintos días), para el día representado en rojo y durante una fracción de la segunda hora para el día “azul”. El resto de los días no produce sombras. El objeto 2 nunca produce sombras. Los días de esta gráfica son días “representativos” del año: solsticio de verano (verde), de invierno (rojo), equinoccios (azul).