RESPUESTAS del Examen de PROCESAMIENTO IMÁGENES / 19

RESPUESTAS del
Examen de PROCESAMIENTO IMÁGENES / 19-IX-2008
1. Determina unos valores de los parámetros, a, b y c, de la transformación
si 0  u  c
0
T (u )  
2
si c  u  1
a  bu
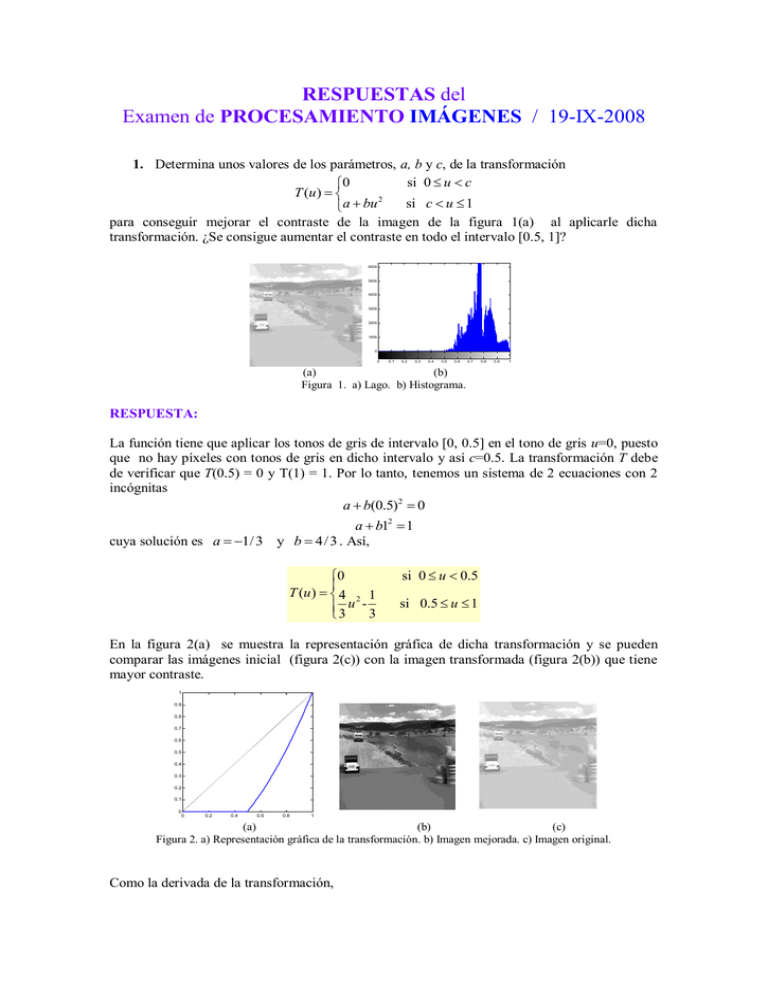
para conseguir mejorar el contraste de la imagen de la figura 1(a) al aplicarle dicha
transformación. ¿Se consigue aumentar el contraste en todo el intervalo [0.5, 1]?
6000
5000
4000
3000
2000
1000
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
(a)
(b)
Figura 1. a) Lago. b) Histograma.
RESPUESTA:
La función tiene que aplicar los tonos de gris de intervalo [0, 0.5] en el tono de gris u=0, puesto
que no hay píxeles con tonos de gris en dicho intervalo y así c=0.5. La transformación T debe
de verificar que T(0.5) = 0 y T(1) = 1. Por lo tanto, tenemos un sistema de 2 ecuaciones con 2
incógnitas
a  b(0.5)2  0
a  b12  1
cuya solución es a  1/ 3 y b  4/ 3 . Así,
0

T (u )   4 2 1
 3 u - 3
si 0  u  0.5
si 0.5  u  1
En la figura 2(a) se muestra la representación gráfica de dicha transformación y se pueden
comparar las imágenes inicial (figura 2(c)) con la imagen transformada (figura 2(b)) que tiene
mayor contraste.
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0
0.2
0.4
0.6
0.8
1
(a)
(b)
(c)
Figura 2. a) Representación gráfica de la transformación. b) Imagen mejorada. c) Imagen original.
Como la derivada de la transformación,
0

T '(u )   8
u

3
si 0  u  0.5
si 0.5  u  1
es mayor que 1 en el intervalo [0.5, 1] resulta que se consigue aumentar el contraste de la
imagen en todo el intervalo de definición.

2. ¿Cómo restaurarías la imagen de la figura 2, movida en la dirección de 45o, a partir de
un filtro de convolución de tamaño 5×5 y utilizando la transformada de Fourier?
(a)
(b)
Figura 3. a) Imagen movida. b) Imagen restaurada.
RESPUESTA:
Una plantilla de tamaño 5×5 que aplicada como filtro produce el efecto de la borrosidad por
desplazamiento en la dirección de 45o es la siguiente:
0
0
0.0501 0.0304 
 0


0
0.0519 0.1771 0.0501 
 0
h 0
0.0519 0.1771 0.0519
0 


0
0 
 0.0501 0.1771 0.0519
 0.0304 0.0501
0
0
0 

Sus elementos suman uno y van disminuyendo conforme nos retiramos del elemento central,
siendo la disminución menor en la dirección de 45o. La imagen borrosa obtenida, fo, mostrada en
la figura 3, correspondería a la convolución de la imagen real, f, con la plantilla h. Es
decir, fo  f  h . Se trata ahora de determinar f conociendo h y fo. Para ello aplicamos la
transformada de Fourier que nos lleva a:
Fo  F  H
Donde Fo, F y H las transformada de Fourier de fo, f y h, respectivamente. De aquí se obtiene
que F  F0 / H y así a transformada de Fourier inversa aplicada a F0 / H nos conduce a f, la
imagen real no distorsionada con la plantilla h, que se muestra en la figura 3(b).

3. ¿Cómo eliminarías las líneas más delgadas de la figura 3(a), sin apenas alterar el resto
de la imagen, mediante filtrado de la imagen, para conseguir la figura 3(b)?
(a)
(b)
Figura 4. a) Circuito. b) Circuito modificado.
RESPUESTA:
Las líneas delgadas se pueden considerar como ruido dentro de la imagen y se eliminan
aplicándole el filtro mediana con una ventana de tamaño, por ejemplo, 5×5, que garantiza que
en un entorno de tamaño 5×5 de un pixel de una línea delgada no haya mayoría de píxeles de
dicha línea, por lo que el filtro mediana sustituirá el tono de gris del píxel de la línea (blanco)
por el valor mediano de los píxeles del entorno (negros). En la figura 4(b) se muestra la imagen
resultante.

4. El filtro de paso baja de Butterworth. ¿Cómo medirías el deterioro (borrosidad) de la
imagen según el valor del parámetro Do seleccionado?
RESPUESTA:
Ver apuntes de clase.

5. Deduce el operador de Laplace como un operador de segundo orden y muestra cómo
cualquier imagen se puede descomponer en suma de dos imágenes, una imagen de bordes y una
imagen borrosa (suavizada). ¿Cuál es el filtro de paso baja complementario al de Laplace?
RESPUESTA:
Ver apuntes de clase.

6. Transformaciones lineales para la compresión de imágenes.
RESPUESTA:
Ver apuntes de clase.

7. Explica con detalle el proceso de segmentación de imágenes que seguirías que seguirías para
determinar el número de monedas que aparecen en la figura 4, así como su tamaño y su posición
en la imagen.
Figura 5. Monedas.
RESPUESTA:
Ver apuntes de clase.
8.- ¿Cómo extraerías el fondo de la imagen de la figura 5 mediante un operador
morfológico? ¿Cómo corregirías el efecto de la iluminación no uniforme en la imagen de
cromosomas?
Figura 6. Cromosomas.
RESPUESTA:
Para extraer el fondo de la imagen de cromosomas se aplica el operador morfológico de
dilatación para imágenes en tonos de gris, es decir, el operador que consiste en sustituir el tono
de gris de cada pixel por el tono de gris mayor que presenten los pixeles de su entorno. Si
tomamos un elemento estructurador de tamaño 20×20 garantizamos que en un entorno de dicho
tamaño de cualquier pixel de un cromosoma haya píxeles del fondo y entonces el tono de gris de
dicho pixel será sustituido por el tono de gris de un pixel del fondo que es más luminoso. De
esta manera se obtiene la imagen de la figura 7.
Figura 7. Fondo de la imagen
Figura 8. Cromosomas.
A la imagen de fondo obtenida, que es más luminosa que la original, se le resta la imagen
original, con lo que se consigue un fondo homogéneo y oscuro puesto que los píxeles del fondo
tienen valores similares en las dos imágenes. Los cromosomas tienen ahora un tono de gris que
es el complementario con respecto al fondo. Por lo tanto, la imagen complementaria de la
imagen diferencia entre la imagen de fondo y la imagen original nos da la imagen de los
cromosomas con un fondo más uniforme (ver la imagen de la figura 8). En la figura 9 se
muestra el programa Matlab que realiza el proceso explicado.
PROGRAMA MATLAB
I=imread('chromos2.tif');
SE=strel('rectangle',[25 25]);
F=imdilate(I,SE);
imshow(F)
R=256-(F-I);
figure,imshow(R)
Figura 9. Programa en Matlab.

RESPUESTAS AL EXAMEN DE
PROCESAMIENTO DE IMÁGENES /01-II-2007
1. Analiza con detalle el efecto que produce la transformación siguiente sobre el contraste de la
imagen digital de la figura 1, cuyos tonos de gris están normalizados en el intervalo [0,1]:
100
4u 2 si 0  u  0.5
T (u )  
si 0.5<u  1
1
50
0
0
0.5
1
Figura 1. Reloj e histograma.
RESPUESTA:
Se trata de encontrar los intervalos donde la función T(u) tiene una pendiente mayor que la
unidad. Como la pendiente viene dada por la derivada de la función, es decir,
dT (u ) 8u si u [0,0.5]

,
si u  (0.5,1]
dt
0
resulta que la pendiente de dicha función es mayor que 1 siempre y cuando u  (1/8,0.5] . Por lo
tanto, en el intervalo de tonos de gris, (1/8,0.5] , se mejora el contraste de la imagen, a costa de
reducirlo en los intervalos restantes, [0,1/8) y (0.5,1] .
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Figura 2. Representación gráfica de la función T(u).
2. Filtros recursivos: si filtramos la imagen de la figura 1 utilizando la plantilla, M1= [¼ ½ ¼],
y a continuación filtramos la imagen resultante con la plantilla,
M2 =
1 / 4
 
1 / 2
1 / 4
 
, ¿cómo es la plantilla equivalente a la aplicación consecutiva de estas dos plantillas?
RESPUESTA:
Sea f(i,j) el tono de gris del píxel (i,j). La aplicación de la plantilla M1 sobre la imagen
transforma el tono de gris del píxel (i,j) según la expresión siguiente (notación cartesiana):
f *(i, j ) 
1
1
1
f (i, j )  f (i  1, j )  f (i  1, j )
2
4
4
La aplicación de la plantilla M2 a la imagen resultante f* transforma el tono de gris del píxel (i,j)
según la expresión siguiente:
f **(i, j ) 
1
1
1
f *(i, j )  f *(i, j  1)  f *(i, j  1)
2
4
4
1 1
1
1
1
1
 1 1

  f (i, j )  f (i  1, j )  f (i  1, j )    f (i, j  1)  f (i  1, j  1)  f (i  1, j  1) 
2 2
4
4
4
4
 4 2

1 1
1
1

  f (i, j  1)  f (i  1, j  1)  f (i  1, j  1) 
4 2
4
4

= M  f (i, j ) , siendo
1/16 1/ 8 1/16 
M   1/ 8 1/ 4 1/ 8 
1/16 1/ 8 1/16 
Es decir, es equivalente a aplicar directamente un filtrado lineal con la plantilla M a la imagen f.
Obsérvese que dicha matriz viene dada por el producto de las respectiva matrices de M2 y M1:
1/4 
1/16 1/ 8 1/16 
 


1/2  (1/ 4 1/2 1/4)   1/ 8 1/ 4 1/ 8 
1/16 1/ 8 1/16 
1/4 


 
3. ¿Qué es un cuantificador? ¿En qué consiste el problema de determinar un cuantificador
óptimo?
RESPUESTA:
Un cuantificador Q (escalar) es una aplicación de  en el conjunto discreto de puntos
C={r1, r2 ,...., rL} llamado tabla de códigos. La cantidad r=log2L se llama resolución y mide el
número de bits necesarios para representar los códigos. Es decir, los niveles de gris de la imagen
muestreada. Por ejemplo, si representamos la intensidad luminosa de una
números
del
conjunto {0,1, ...., 255}, tenemos
imagen f(x,y) por
una resolución r=log2256=8. Cada
cuantificador de L puntos tiene asociada una partición de  en L regiones Ri
i=1,2, .... L,
definidas por la expresión:
Ri= { t : Q (t) = ri }, i=1,2,…,L.
L
de manera que
 Ri  , Ri  R j  , i  j .
i 1
La intensidad luminosa se puede representar mediante una variable aleatoria U que toma
valores en
el conjunto { f(x,y): (x,y)} con función de densidad pU(u). Dicha función de
densidad se puede estimar por las frecuencias relativas de los tonos de gris. El problema de
determinar un cuantificador óptimo consiste en determinar los niveles de transición ti y los
niveles de reconstrucción ri de tal manera que se minimice el error cuadrático medio
ECM  E (U  U ')  
2
tL1
 (u  u ')
2
 pU (u ) u
t1
donde U' es la variable aleatoria, U’ = Q(U), y E es el operador esperanza matemática (media)
de una variable aleatoria. La expresión anterior se puede escribir también como
L ti 1
ECM    (u  ri )2  pU (u ) du
i 1 ti
4. Disponemos de una imagen digital, I, distorsionada mediante un filtro lineal de paso baja
cuya plantilla h es conocida. ¿Cómo obtendrías la imagen original no distorsionada?
RESPUESTA:
La nueva imagen distorsionada mediante un filtro de paso baja cuya plantilla es h viene dada
por la siguiente expresión:
  

I 0 (m, n)     h(m  k , n  j )  I (k , j )  ,
 k  j 

El problema de la reconstrucción de la imagen inicial I a partir de la imagen distorsionada
I0(m,n), consiste en determinar la función de restauración hR(m,n) que nos proporcione una
estimación de la imagen original a través de la expresión:
I (m, n) 


  h (m  k , n  j )  I
k  j 
R
0
(k , j )
 hR (m, n)  I 0 (m, n)
 hR (m, n)   h(m, n)  I (m, n)
Si aplicamos la transformada de Fourier, tenemos
FI (u, v)  H R (u, v)   H (u, v)  FI (u, v)
Si ahora elegimos como función de reconstrucción aquella cuya transformada de Fourier es la
inversa de la transformada de Fourier de la plantilla de paso baja h, es decir,
H R (u, v) 
1
H (u, v)
Por lo tanto, se obtiene que FI (u, v)  FI (u, v) .
Es decir, I  I . Por lo tanto, se puede reconstruir la imagen distorsionada sin más que tomar
como función de reconstrucción aquella cuya transformada de Fourier es la inversa de la
transformada de Fourier de la plantilla correspondiente al filtro de pasa baja.
5. La modulación delta: Transformación, cuantificación y codificación. ¿Qué ocurre si se elige
un valor de delta demasiado pequeño?
RESPUESTA:
Apuntes de la asignatura
6. Los descriptores de Fourier: ¿Qué interpretación tienen? ¿Para que son útiles? ¿Qué
propiedades tienen sus magnitudes y sus fases?
1 N 1
2 nui
Z (u )   z (n)exp(
)
N n 0
N
RESPUESTA:
Apuntes de la asignatura
7. Explica la transformada de Hough para la detección de objetos cuadrados de la figura 3,
teniendo en cuenta que un cuadrado de centro (a, b) y longitud de lado 2l viene descrito por la
ecuación:
max  ( x  a , y  b   l
Figura 3. Tarjeta gráfica.
RESPUESTA:
La transformada de Hough de un punto (x1, y1) del espacio cartesiano XY se hace corresponder
al cuadrado de centro dicho punto y lado 2l en el espacio paramétrico de cuyos ejes de
coordenadas corresponden a los parámetros a y b.
Max  x1  a , y1  b   l
Si un punto (a1,b1) del espacio paramétrico es intersección de n cuadrados con longitud del lado
2l quiere decir que hay n puntos (x1, y1), (x2, y2),…, (xn, yn), que son los centros de los mismos y
que verifican:
Max  xi  a1 , yi  b1   l , i=1,2,…,n.
Por lo tanto, dichos puntos pertenecen a un cuadrado del espacio cartesiano de centro (a1,b1) y
lado 2l.
En consecuencia, las intersecciones de los cuadrados en el espacio paramétrico corresponde a
los centro de cuadrados en el espacio cartesiano.
Algoritmo para determinar cuadrados:
Paso 0: Poner a cero los contadores A(a,b,l).
Paso 1: Para a = a1, a2,….,ar realizar los pasos siguientes.
Paso 2: Para b = b1, b2,….,bs realizar los pasos siguientes.
Paso 3: Para i = 1, 2, …, n, determinar
l  Max  xi  a , yi  b 
e incrementar el contador: A(a,b,l) = A(a,b,l) +1.
fin
fin
fin
fin
Paso 4: Identificar los contadores cuyo valor es superior a un valor umbral t (t es el número
mínimo de puntos que deben configurar un cuadrado para que se considere como tal). Los
parámetros de estos contadores corresponden a los centros y a la mitad de las longitudes de los
lados de los cuadrados encontrados.
8. ¿Cómo determinarías el número de arandelas que hay en la imagen de la figura 4 que tienen
un radio interior de 3 píxeles y exterior de 6 píxeles, utilizando operadores morfológicos?
Figura 4. Arandelas.
RESPUESTA:
Mediante el operador de aciertos y fallos (hit-miss). Para ello utilizamos dos elementos
estructurantes disjuntos, g1 y g2. El primero se utiliza con el operador erosión para determinar
los píxeles en los que coinciden todos los unos del elemento estructurante con unos en la
subimagen correspondiente centrada en ellos. El segundo se utiliza también con el operador
erosión aplicado al negativo de la imagen f para identificar los píxeles en los que coinciden los
unos del elemento estructurante g2 con unos del negativo de la subimagen correspondiente
centrada en ellos. Por lo tanto, el operador de aciertos y fallos viene dado por la expresión
f  g  ( f g1 )  ( f g2 )  ( f g1 )  ( f  g2 )
En este problema utilizaríamos como elemento estructurantes g1 el correspondiente a la plantilla
de la figura 5 y como elemento estructurante g2 el que se presenta en la figura 6.
Figura 5. Elemento estructurante g1.
Figura 5. Elemento estructurante g2.
RESPUESTAS AL EXAMEN DE
PROCESAMIENTO DE IMÁGENES /15-II-2006
1. Define analíticamente la transformación de tramos lineales que utilizarías para mejorar el
contraste de la imagen de la figura 1(a) en los intervalos de tonos de gris [0, 50] y [100, 180] a
costa de anular el contraste en los intervalos restantes.
(a)
(b)
(c)
Figura 1. a) Fotógrafo. b) Histograma de la imagen. c) Imagen mejorada.
RESPUESTA:
La transformación de tramos lineales puede ser la siguiente:
si
0  u  50
2u
100
si 50  u  100

T (u )  
155
100  80 (u  100) si 100  u  180

si 180  u  255
255
puesto que incrementa el contraste en el intervalo [0, 50] por tener la transformación pendiente
dos, que es mayor que uno, y en el intervalo [100, 180] por tener pendiente 155/80, que también
es mayor que uno. En los intervalos restantes la pendiente es cero por lo que se anula el
contraste al asignarle el mismo tono de gris a todos los puntos de dichos intervalos.
La figura 2 muestra la representación gráfica de dicha transformación.

Figura 2. Gráfica de la transformación T(u).
2. Cuando se reduce el tamaño de una imagen se suele producir un efecto conocido como
“aliasing” que consiste en la aparición de contornos escalonados o rizados, sobre todo en las
zonas de alto contraste de la imagen (figura 3). ¿Cómo reducirías una imagen de tamaño
256256 a tamaño 6464 de manera que se atenúe el efecto “aliasing”?
(a)
(b)
Figura 3. a) Imagen de reloj después de la
reducción directa. b) Imagen deseada.
RESPUESTA:
Se divide la imagen en bloques (ventanas) de píxeles de tamaño 44 y se sustituye cada ventana
por un píxel que tiene como tono de gris el valor medio o el valor mediano de los tonos de gris
de los píxeles de dicha ventana. Sin embargo, dicha reducción puede producir el efecto de
“aliasing” en las zonas de más alto contraste. Una forma de atenuarlo consiste en suavizar
previamente la imagen utilizando un filtro de paso baja, como puede ser el filtro gaussiano.

3. ¿Cómo eliminarías las rayas o las líneas delgadas de una imagen (figura 4) mediante filtrado
sin apenas alterarla y sin introducir ruido? ¿Cómo eliminarías sólo las rayas verticales?
Figura 4. Ojo humano.
RESPUESTA:
Se utiliza un filtro mediana cuya plantilla tenga un tamaño tal que al aplicarlo sobre los píxeles
de la raya siempre haya en el entorno que define la plantilla un número superior del píxeles que
no sean píxeles de la raya. De esta forma el tono de gris de cada píxel de una raya se sustituye
por el tono de gris correspondiente al valor mediano de los tonos de gris de los píxeles que
cubre la plantilla.
En el caso de rayas verticales se utiliza un filtro mediana cuya plantilla es de tamaño 1m
(m3).

4. ¿Qué propiedades caracterizan a un píxel del contorno de un objeto, o de su interior, en
términos de sus 8 vecinos en un entorno 33? Identifica el contorno de los objetos (perímetro)
de la figura 5 a partir de un filtrado lineal por convolución con una plantilla de tamaño 33.
(a)
(b)
Figura 5. a) Imagen binaria de un circuito.
b) Contorno de los objetos.
RESPUESTA:
Un píxel interior de una imagen binaria se puede definir como aquel cuyo entorno 33 contiene
todos sus píxeles con el mismo tono de gris. Un píxel es del contorno si alguno de los píxeles de
su entorno 33 presenta un tono de gris diferente del suyo.
Si suponemos que los objetos se corresponden con píxeles blancos y el fondo con píxeles
negros, podemos determinar el conjunto de píxeles interiores de los objetos mediante un filtro
de paso baja cuya plantilla tiene tamaño 33 y todos sus elementos valen 1/9.
1/ 9 1/ 9 1/ 9 
g  1/ 9 1/ 9 1/ 9 
1/ 9 1/ 9 1/ 9 
La imagen filtrada tiene un valor igual a uno para todos los píxeles interiores de los objetos, un
valor cero para los píxeles interiores del fondo y un valor del intervalo [1/9, 8/9] para los píxeles
del contorno. Por lo tanto, un píxel del contorno viene caracterizado por que su tono de gris en
la imagen filtrada pertenece a dicho intervalo. Si se desea una representación gráfica del
contorno sobre un fondo negro (figura 5b) basta con realizar la siguiente transformación sobre la
imagen obtenida:
1 8

si u  [ , ]
1
T (u )  
9 9

0
en
otro
caso

8.- Define el operador morfológico TopHat para imágenes monocromáticas (en tonos de
gris). ¿Cómo sería la imagen resultante al aplicarle dicho operador a la imagen de la figura 5
con un elemento estructurante que no está contenido en ningún grano de arroz de la imagen.
Figura 6. Imagen de granos de arroz.
RESPUESTA:
El operador morfológico TopHat viene definido por la expresión:
TopHat ( f )  f  f  g

donde f  g   f g   g , ( f g )(m, n)  min f (m  i, n  j )  g (i, j ) (i, j )  Dg

( f  g )(m, n)  max f (m  i, n  j )  g (i, j ) (i, j )  Dg


y
Si aplicamos el operador erosión (MÍNIMO), con un elemento estructurante de tamaño dado,
sobre un píxel de un objeto pueden ocurrir tres cosas:
a) Que el elemento estructurante quede contenido en el objeto, en cuyo caso el nuevo
valor del píxel será el tono de gris mínimo de los píxeles de dicho objeto cubiertos por
la plantilla. En este caso el píxel del objeto no pasa a ser un píxel del fondo. Por lo tanto
no queda eliminado totalmente el objeto (no se confunde con el fondo).
b) Que el elemento estructurante cubra completamente al objeto, es decir, que al aplacar el
operador erosión con dicho elemento estructurante siempre se coge algún píxel del
fondo (más oscuro) y, por lo tanto, sustituirá su tono de gris por un tono de gris del
fondo. En este caso el objeto se convierte en fondo (queda eliminado).
c) Que no ocurra ninguno de los casos anteriores. Al aplicar el operador erosión sobre un
píxel de un objeto concreto lo transforma en un píxel del fondo, puesto que para que se
transforme en un píxel del objeto es necesario que todos los píxeles de la plantilla sean
del objeto (caso (a)).
En el caso a) si aplicamos el operador abertura obtendríamos la imagen de la figura 7 donde
los objetos que contienen a la plantilla asociada al elemento estructurante no ha quedado
eliminados. Obsérvese que al aplicar primero la erosión se eliminan (o atenúan) los granos
de arroz “pequeños”, es decir, los que no contiene a la plantilla. Al aplicar el operador de
dilatación (MÁXIMO) los granos de arroz recuperan su tamaño original pero cogiendo la
forma cuadrada de la plantilla utilizada (figura 7).
Figura 7. Imagen f g.
Figura 8. Imagen f f g.
Si a la imagen original de la figura 6 le restamos la imagen obtenida (figura 7) se obtiene la
imagen de la figura 8 que viene caracterizada por un fondo uniforme y constituida por los
granos de arroz más pequeños.
En los casos b) y c) el operador erosión f g nos genera una imagen del fondo, ya que el tono
de gris de cada píxel es sustituido por el tono de gris mínimo del entorno determinado por el
elemento estructura que siempre contendrá píxeles del fondo (oscuro). En la figura 9 se presenta
la imagen obtenida que revela una iluminación no uniforme en la imagen original. La parte
inferior de la imagen está más oscura (menos iluminada). Al aplicarle a continuación el
operador dilatación se obtiene una imagen del fondo un poco más luminosa (figura 10).
Figura 9. Imagen fg.
Figura 10. Imagen ( fg)g.
Al restarle a la imagen original dicha se obtiene la imagen de la figura 11 cuya iluminación es
uniforme y contiene a todos los objetos.

Figura 11. Imagen final uniforme.
E. T. S. I. Informática
Universidad de Málaga
RESPUESTAS del Examen de
PROCESAMIENTO DE IMÁGENES
/ 16-II-2005
1. ¿Qué efecto produce sobre el contraste de la imagen de la figura 1 la transformación y=x3,
cuya gráfica se muestra en la figura 1, suponiendo que sus tonos de gris están normalizados en
el intervalo [0,1]? Indica los tonos de gris en los que se mejora el contraste y en los que se
empeora.
Figura 1. a) Transformación cúbica. b) Mamografía.
Respuesta:
Hay que analizar los puntos donde la pendiente de la curva es mayor que uno, pues en ellos se
aumenta el contraste de la imagen, a costa de reducirse en los puntos de menor pendiente.
Como la pendiente viene dada por la tangente a la curva, es decir, su derivada, resulta que
y '  3x 2  1  x 2 
Por lo tanto, para x 
1
3
1
3
se obtiene una pendiente mayor o igual a uno y, por tanto, un
 1 
aumento del contraste de la imagen en el intervalo  `,1 a costa de reducirlo en el intervalo
 3 
 1 
0, ` .
3

2.- Indica un procedimiento para obtener el contorno de los objetos de la imagen de la figura
2(a) para conseguir la imagen de la figura 2(b) utilizando un filtro no lineal.
Figura 2. a) Objetos. b) Contornos.
Respuesta:
Como en la imagen de la figura 2 los objetos son oscuros con un fondo más claro podemos
utilizar el filtro MAX de tamaño 33 pues en los píxeles del contorno de los objetos toma el
valor de fondo y así produce una erosión de los mismos. Si le restamos a la imagen resultante la
imagen original conseguiremos la imagen del contorno de los objetos. Aplicando el operador
umbral con el valor umbral que sea inferior al valor mínimo del fondo conseguiremos la imagen
binaria de la figura 2(b).
Una manera más eficiente computacionalmente es aplicar primero el operador umbral
complementario
si f ( m, n)  t
0
T ( f (m, n))  
si f (m, n)  t
1
siendo t un valor entre el valor inferior al valor mínimo del fondo. La imagen que se obtiene es
binaria con los objetos blancos y el fondo negro. Le aplicamos el filtro MIN de tamaño 33,
pues en los píxeles del contorno de los objetos toma el valor de fondo negro y así produce una
erosión de los objetos. Restando a la imagen original la imagen transformada conseguimos la
imagen del contorno de los objetos en blanco con fondo negro. Finalmente, la imagen de la
figura 2(b) se obtiene como la complementaria (negativo) de la imagen conseguida.
f(m,n)
f(m,n)
UMBRAL T
MIN33
DIFERENCIA
NEGATIVO
t
3. La imagen de la figura 3 corresponden a una fotocopia (dos cuadrados sobre un fondo gris)
que ha sufrido un oscurecimiento progresivo al no colocarse bien el soporte que presiona sobre
el cristal a la imagen original. ¿Cómo restaurarías dicha imagen suponiendo que la última
columna de la matriz asociada a la imagen obtenida corresponde a los valores correctos.
Figura 3. Fotocopia.
Respuesta:
Se trata de una imagen con iluminación no uniforme. Por lo tanto, en primer lugar vamos a
obtener el fondo de la imagen ya que contiene la información del oscurecimiento progresivo de
derecha a izquierda. Como el fondo es más oscuro que los objetos utilizamos el operador MIN
con una plantilla cuyo tamaño garantice que al aplicarlo sobre una píxel cualquiera contenga
píxeles del fondo. Como la imagen es de tamaño 222285 se puede tomar, por ejemplo, una
plantilla de tamaño 7419. Se obtiene la siguiente imagen:
Figura 4. Imagen del fondo
A continuación se resta a la imagen original la imagen del fondo, con lo cual se obtiene una
imagen con iluminación uniforme, como se muestra en la figura 5 (después de una suavización).
Figura 5. Imagen con iluminación uniforme.
Finalmente, se puede conseguir una imagen realzada aplicando la igualación del histograma,
como se muestra en la figura 6.
Figura 6. Imagen final.
6. ¿Cómo detectarías la posición de la planta química (edificio grande de color blanco) de la
figura 7 mediante el método de segmentación basado en las proyecciones?
Figura 7. a) Imagen aérea. b) Histograma.
Respuesta:
Se determinan las proyecciones de la imagen sobre los ejes de coordenadas,
256
pi   f (i, j ) y
j 1
256
p j   f (i, j ) ,
i, j = 1,2,…,256
i 1
cuyas representaciones gráficas se representan en las figuras 8 y 9, respectivamente.
Figura 8. Gráficas de las proyecciones verticales.
Figura 9. Gráficas de las proyecciones verticales.
A partir de los valores máximos de las proyecciones se identifica la planta química que es el
objeto más claro, como se muestra en la figura 10.
Figura 10. Identificación de la planta basada en las proyecciones.
8. Determinación de la distribución del tamaño de los objetos pequeños (partículas) de
una imagen en tonos de gris (figura 11) mediante operadores morfológicos.
Figura 11. Nódulos.
Respuesta:
Se trata de determinar la distribución de los objetos según su tamaño. En primer lugar pasamos
a una imagen binaria aplicando el operador umbral. Se obtiene la imagen de la figura 12.
Figura 12. Figura original binaria
Como los objetos son negros y el fondo es blanco se aplica el operador cierre con elementos
estructurantes circulares de diferente radio. Al aplicar el operador cierre con un elemento
estructurante de radio r vamos a obtener una imagen en la que se eliminan los objetos
contenidos en círculos de radio inferior a r. Si aplicamos dicho operador cierre sucesivamente,
incrementando los valores de r, y restamos a cada imagen obtenida la anterior, vamos
obteniendo las imágenes que contienen sólo a los objetos de un tamaño determinado, es decir,
que están contenidos en círculos de radio r+1 pero no están contenidos en círculos de radio r.
Por ejemplo, si aplicamos el operador cierre con elementos estructurantes circulares, cuyos
radios son 5, 6, 7, 8, 9, 10, 11, 12, 13 y 14, obtenemos la imagen (a) de la figura 13 para r=5, la
imagen (b) para r=6, la imagen (c) para r=7, la imagen (d) para r=8, la imagen (e) para r=9, la
imagen (f) para r=10, la imagen (g) para r=11, 12 y 13, y la imagen (h) para r=14, la imagen
(d).
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Figura 13. Figura 11. (a) Imagen resultante al aplicar el operador cierre con un disco de radio 5. (b)
Con un disco de radio 6. (c) Con un disco de radio 7. (d) Con un disco de radio 8. (e) Con un disco de
radio 9. (f) Con un disco de radio 10. (g) Con un disco de radio 11, 12 ó 13. (h) Con un disco de
radio 14 ó 15.
Si a continuación restamos a la imagen obtenida aplicando el operador cierre con el elemento
estructurante de radio r+1 la imagen obtenida al aplicarlo con radio r obtenemos una imagen
con sólo los objetos de “tamaño r” pues están contenidos en un disco de radio r+1 y no los
cubre uno de radio r. Por ejemplo, si restamos a d) la imagen c) obtenemos la imagen de la
figura 14 que contiene sólo los elementos de radio 7 (menor que 8).
Figura 14. Imagen con los nódulos de tamaño 7.
Para obtener la distribución según el tamaño de los objetos se determina la suma de los valores
(tonos de gris) de todos los píxeles de la imagen obtenida por diferencia con la imagen anterior;
dicha suma es el área de los objetos de la misma. Podemos representar gráficamente el área de
cada una de las superficies obtenidas frente al radio de los elementos estructurantes (discos).
Además, si los objetos tienen la forma del elemento estructurante empleado, como ocurre en
este caso, y el área de cada objeto es r2, podemos determinar el número de objetos que hay en
la imagen sin más que dividir el área total por el tamaño del objeto. Por lo tanto, se obtiene la
distribución de los nódulos según su tamaño que se muestra en la tabla I.
Radio de los
objetos
5
6
7
8
9
10
11
12
13
14
15
Nº de
objetos
24
25
9
2
1
2
0
0
1
0
3
Tabla I. Distribución de los nódulos de radio superior a 4.
También podemos representar gráficamente el área total de los objetos de cada imagen obtenida
mediante el operador cierre con los distintos valores del radio del elemento estructurante. Dicha
gráfica se muestra en la figura 15.
Figura 13. Representación gráfica del área total de los
objetos frente al radio del elemento estructurante.
Como se puede observar, el mayor número de objetos corresponde a los objetos de menor
tamaño. Los máximos locales de la función indican una mayor abundancia de los objetos del
tamaño correspondiente frente a los objetos de tamaño más próximo.
E. T. S. I. Informática
Universidad de Málaga
Examen de PROCESAMIENTO DE IMÁGENES /
9-II-2005
1.
Define la transformación de tramos lineales que utilizarías para mejorar el contraste de la
imagen de la figura 1(a) cuyos tonos de gris están concentrados en el intervalo [30,235].
Figura 1. a) Aeropuerto. b) Histograma de la imagen.
Respuesta:
Teniendo en cuenta la forma del histograma se puede utilizar una función continua de tramos
lineales cuyas pendientes en el intervalo [30, 235] sean mayores que uno para aumentar el contraste
en dicho intervalo en el que están concentrados los tonos del gris de la imagen. La pendiente será
mayor cuanta más concentración de píxeles haya en el intervalo correspondiente.
0

1.3 f (m, n)  30
f * (m, n)   99
  f (m, n)  150  156
 85
 255
si
f (m, n)  30
si 30  f(m,n)  150
si 150  f (m, n)  235
si 235  f ( m, n)  255
Fig. 2. Transformación de tramos lineales.
2. ¿Cómo eliminarías las rayas o las líneas delgadas de una imagen (figura 3) mediante filtrado sin
apenas alterarla y sin introducir ruido? ¿Cómo eliminarías sólo las rayas verticales?
Respuesta
Se puede utilizar un filtro mediana de tamaño 33 para eliminar las rayas delgadas si en cada
entorno de tamaño 33 de los píxeles que configuran las líneas delgadas hay cuatro, o menos de
cuatros, píxeles de la línea, como se muestra en la figura 4.
Figura 3. Ojo humano.
Figura 4. Entorno 33.
Análogamente, las rayas verticales se pueden eliminar mediante un filtro mediana de tamaño 13.
3. Filtrado en el dominio de las frecuencias: El filtro de paso alta de Butterworth.
Respuesta: Apuntes de clase
4. Detección del iris (figura 2) mediante la transformada de Hough. ¿Cuál es la principal ventaja
del método basado en la transformada de Hough?
Respuesta: Apuntes de clase
5. Los descriptores de Fourier: ¿Qué interpretación tienen? ¿Para que son útiles? ¿Qué
propiedades tienen sus magnitudes y sus fases?
1 N 1
2 nui
Z (u )   z (n)exp(
)
N n 0
N
Respuesta: Apuntes de clase
6. Segmentación basada en regiones: Divisiones y uniones.
Respuesta: Apuntes de clase
7. El operador morfológico copa de sombrero (Top-Hat): Defínelo e indica para qué se puede
utilizar en la imagen de la figura 1.
Respuesta: Apuntes de clase
8.- Propón una medida de la rectangularidad de un objeto basada en el rectángulo base. Explica
por qué es adecuada.
Figura 3. Rectángulo base de un objeto.
Respuesta:
Si representamos por a y b las longitudes de los lados del rectángulo base que contiene al
objeto, una medida razonable para medir la rectangularidad viene dada por el cociente
entre el área de objeto, que representaremos por A, y el área del rectángulo dada por ab, es
decir:
Rectangularidad =
A
ab
E. T. S. I. Informática
Universidad de Málaga
Examen de PROCESAMIENTO DE IMÁGENES / 4-II-2004
1. ¿Qué transformación de tramos lineales utilizarías para aumentar todo lo que se pueda el
contraste en la imagen digital de la figura 1?
(a)
(b)
Figura 1. (a) Tomografía axial del cráneo. (b) Histograma de la imagen.
Respuesta:
Se puede utilizar la transformación de tramos lineales siguiente (ver la figura 2):
0
2 f (m, n)  0.65

f * (m, n)  
4 f (m, n)  0.70  0.10

  f (m, n)  0.90  0.90
f (m, n)  0.65
si
si 0.65  f(m,n)  0.70
si 0.70  f (m, n)  0.90
si 0.90  f (m, n)  1
f*(m,n)
f(m,n)
Figura 2. Transformación de tramos lineales.
2. Explica las características de la imagen filtrada con la plantilla [1 1 1 1 1]. ¿Conservaría
las altas frecuencias?
Respuesta:
La plantilla se puede descomponer de la forma
[1 1 1 1 1] = [0 0 1 0 0 ] + [1 1 0 1 1]
Por lo tanto, la imagen resultantes correspondería a la imagen original más una imagen
correspondiente a las aristas verticales y así será como la imagen original pero con los bordes
verticales resaltados. Por lo tanto, es una plantilla para el realzado de dicha imagen.
3. Una imagen digital se degrada (filtra) utilizando la siguiente plantilla:
0
0
0
0
0
0.03
0.07
0
0
0
0
0
0
0 0.03
0.03 0.1
0.1 0.03
0.03
0
0
0
0.03
0.1
0.03
0
0
0
0.03
0.1
0.03
0
0
0
0.03 0.07
0.1 0.03
0.03 0
0
0
0
0
0
0
0
0
a) ¿ Qué tipo de borrosidad produce sobre la imagen
original?
b) ¿ Cómo se obtendría la imagen original a partir de
la imagen degradada?
Respuesta:
a) La borrosidad corresponde al efecto de un movimiento relativo en la dirección de 45º a poca
velocidad puesto que sólo afecta a los píxeles de un entorno 77.
b) Sea F(u,v) la transformada de Fourier discreta de la imagen digital y H(u,v) la transformada
de Fourier de la plantilla 77 que provoca el efecto de borrosidad. Como la transformada de
Fourier de la imagen distorsionada con dicha plantilla viene dada por la expresión:
F*(u,v)=F(u,v)H(u,v)
resulta que la imagen original se obtiene aplicando la transformada de Fourier inversa a la
expresión
F*(u,v)[H(u,v)]-1
4. (Ver apuntes de clase)
5. ¿Cómo detectarías la textura de una imagen constituida por dos elementos de textura de
tamaño 3232 que se repiten según se muestra en la figura 3.
Figura 3. Textura.
Respuesta:
Mediante la matriz de relación espacial tomando como relación espacial la siguiente:
R0,64 :
(i, j)  (i , j+64)
R64,0 :
(i, j)  (i+64 , j)
o bien,
Dicha matriz va a tener sus elementos positivos en la diagonal principal.
6. Segmentación: Explica la transformada de Hough para encontrar los objetos cuadrados de
la imagen digital de la figura
Respuesta:
La ecuación de un cuadrado con centro (a,b) y lado l viene dada por la expresión:
l
(1)
Maxx  a , y  b  
2
La transformada de Hough de un punto (x1, y1) del espacio cartesiano XY se hace corresponder
al cuadrado de centro dicho punto y lado l en el espacio paramétrico de cuyos ejes de
coordenadas corresponden a los parámetros a y b.
l
Maxx1  a , y1  b  
2
Si un punto (a1,b1) del espacio paramétrico es intersección de n cuadrados de lado l quiere decir
que hay n puntos (x1, y1), (x2, y2),…, (xn, yn), que son los centros de los mismos y que verifican:
l
Maxxi  a1 , yi  b1   , i=1,2,…,n.
2
Por lo tanto, dichos puntos pertenecen a un cuadrado del espacio cartesiano de centro (a1,b1) y
radio l.
En consecuencia, las intersecciones de los cuadrados en el espacio paramétrico corresponde a
los centro de cuadrados en el espacio cartesiano.
Algoritmo para determinar cuadrados:
Paso 0: Poner a cero los contadores A(a,b,l).
Paso 1: Para a = a1, a2,….,ar realizar los pasos siguientes.
Paso 2: Para b = b1, b2,….,bs realizar los pasos siguientes.
Paso 3: Para i = 1, 2, …, n, determinar
l  2Maxxi  a , yi  b 
e incrementar el contador: A(a,b,l) = A(a,b,l) +1
Paso 4: Identificar los contadores cuyo valor es superior a un valor umbral t (t es el número
mínimo de puntos que deben configurar un cuadrado para que se considere como tal). Los
parámetros de estos contadores corresponden a los centros y longitudes de los dados de los
cuadrados encontrados.
7. Describe un algoritmo que a partir de la imagen 1 nos determine la imagen 2 donde sólo
aparecen los nódulos cuyo radio tiene una longitud inferior a 8 píxeles.
(a)
(b)
(c)
Figura 4. a) Imagen de nódulos. b) Histograma. c) Nódulos de tamaño superior a 8 píxeles.
Respuesta:
Paso 1: Convertir la imagen a binaria mediante el operador umbral con parámetro t=150 (ver
histograma) y determinar su complementaria (fondo negro):
Figura 5. Imagen binaria.
Paso 2: Aplicar el operador erosión con un elemento estructurante circular de radio 8 (plantilla
1717):
Figura 6. Imagen erosionada.
Paso 3: Aplicar el operador dilatación con un elemento estructurante circular de radio 8
(plantilla 1717):
Figura 7. Imagen dilatada.
Paso 4: Restar a la imagen de la figura 5 la imagen de la figura 7:
8. ¿Cómo identificarías una arandela partida, como las mostradas en la figura 5, en una imagen
de constituida por diferentes objetos?
Figura 5. Arandelas partidas.
Respuesta:
Mediante el índice de circularidad dado por la expresión:
C  4
área
 perímetro2
Si r es el radio menor de la arandela y R es su radio mayor, resulta que:
área de la media arandela = (R2 r2)/2
perímetro de media arandela = R + r + 2(Rr)
C
2
Rr 4 Rr


1
Rr  Rr
Si R=2r entonces
C
6 2
=0.71.
9 2  3  4
E. T. S. I. Informática
Universidad de Málaga
Examen de PROCESAMIENTO DE IMÁGENES /
5-II-2003
1. ¿Qué transformación puntual utilizarías para aumentar todo lo que se pueda el
contraste en la región de interés señalada con un recuadro en la imagen digital de la figura
1 (que tiene 256 tonos de gris)?
Figura 1. Región de interés de una galaxia.
Respuesta:
Se trata de aumentar el contraste de la imagen en la zona más iluminada (blanca) de la
galaxia a costa de reducirlo o anularlo en el resto de la imagen. Teniendo en cuenta que los
tonos de gris de la imagen de interés varían aproximadamente entre 100 y 200, como se
observa en el histograma de la figura 4, la transformación puntual más sencilla para
conseguir el objetivo es la siguiente (ver figura 5):
0

T (u )   256
(u  100)

100
si u  100, 200
si u  100,200
Figura 4. Imagen de interés y su histograma
Figura 5. Transformación puntual y la imagen resultante
2. Calcula la transformada de Fourier discreta del filtro cuya plantilla es [-1 0 1]. Si
F(u,v) es la transformada de Fourier discreta de la imagen digital f(m, n) ¿Cuál sería la
transformada de Fourier discreta de la imagen filtrada? La figura 2(b) muestra el espectro
de frecuencia |F(u, v)| de f(m,n).
Figura 2. a) Imagen de Saturno. b) Imagen espectral.
Respuesta:
La transformada de Fourier discreta se determina de la siguiente manera:
1 0
1 0
 2i ( u  v )
 2i ( u  v ) 
1
3
1
H (u, v)  (1)e
e 3 1 
3

2iu
2iu

1 
 e 3  e 3 
3

2
2
  isen( u ) .
3
3
Figura 6. Espectro de Fourier
En la figura 6 se representa gráficamente el espectro de Fourier |H(u,v)|. Como se puede
observar corresponde a un filtro de paso alta.
Si F(u,v) es la transformada de Fourier de una imagen digital f(m,n), entonces la
transformada de Fourier de la imagen filtrada por H(u,v) es la siguiente:
F * (u, v)  F (u, v) H (u, v) ,
puesto que la transformada de Fourier de la convolución de funciones es el producto de las
transformadas de Fourier de dichas funciones.
3. Hemos capturado una imagen digital fo(m, n) que corresponde a una imagen digital
f(m, n) distorsionada por convolución mediante una función de degradación h(m, n), sin
ruido adicional. Encuentra la función de reconstrucción g(m, n) que permite reconstruir de
forma exacta, por convolución, la imagen digital original f(m, n).
Respuesta
Como la imagen digital fo(m, n) corresponde a la imagen digital f(m, n) distorsionada por
convolución con la función de degradación h(m, n), resulta que:
f o (m, n)   h(i, j ) f (m  i, n  j )
i
i
Su transformada de Fourier discreta es
Fo (u, v)  H (u, v) F (u, v)
Ahora se trata de encontrar una función de reconstrucción g(m, n) tal que
f (m, n)   g (i, j ) f o (m  i, n  j ) .
i
i
Si tomamos la transformada de Fourier en la expresión anterior, se tiene que dicha
condición es equivalente a que
F (u, v)  G(u, v) Fo (u, v)
Por lo tanto, basta con tomar como función de reconstrucción aquella cuya transformada de
Fourier discreta es la inversa de H, es decir,
G(u,v)=1/H(u,v).
4. Determina los bordes da la imagen de la figura 3
utilizando un método basado en un operador no lineal.
Figura 3. Columna vertebral
Respuesta
Podemos utilizar el operador MIN con una plantilla 3x3, que sustituye el tono de gris de
cada píxel por el valor mínimos de tono de gris de los píxeles de su entorno 3x3. Segiremos
el diagrama de operaciones que se muestra en la figura 7; restamos a la imagen original la
imagen resultante y obtenemos la imagen de bordes. Para poderla ver mejor le aplicamos el
operador umbral al nivel 4 (ver el histograma de la imagen diferencia en la figura 8(a)) y
obtenemos la imagen de bordes que se muestra en la figura 8(b).
f(m,n)
DIFERENCIA
MIN
UMBRAL
t=4
Imagen
de
Bordes
Figura 7. Diagrama de Operaciones
(a)
(b)
Figura 8. (a) Histograma de la imagen diferencia.
(b) Imagen de bordes.
5. Define el filtro ideal de paso baja en el dominio de las frecuencias. ¿Cómo
determinarías su radio r para conseguir una potencia del 95%.
Respuesta:
Viene recogida en los apuntes de clase.
6.- El operador erosión con el elemento estructurante 3x3 (todos unos) se aplica
sucesivamente en una imagen binaria con un solo objeto hasta que este desaparece. Sea d el
número de veces que se ha aplicado dicho operador. Construye un descriptor de forma
basado en dicho valor d y en el área A del objeto para medir cómo de alargado es el objeto.
Respuesta:
Si a un objeto de una imagen binaria con fondo negro le aplicamos el operador erosión con
un elemento estructurante cuadrado de tamaño 3x3 se obtiene una nueva imagen que ha
perdido los píxeles de su contorno. Si volvemos a aplicar dicho operador la imagen se sigue
reduciendo. En el caso de un círculo de radio r, desaparece después de r aplicaciones del
operador. Para una figura de igual área que el círculo pero más alargada necesitaríamos
aplicar el operador erosión un número menor de veces para eliminar el objeto. Por ejemplo
una región cuadrada de tamaño 3x100 desaparecería después de aplicar dos veces dicho
operador. Por lo tanto, d es menor cuanto más delgado sea el objeto, siempre comparando
objetos con igual área, y así es una media del grosor máximo del objeto. Por lo tanto, una
media de cómo de alargado (delgado) es un objeto, puede ser
I1 
área
d2
Se divide por el cuadrado de d en lugar de dividir simplemente por d para conseguir una
medida adimensional. Sin embargo, esta medida no está normalizada (acotada). Por
ejemplo, para un círculo vale π y para un rectángulo 2xL vale 2xL (proporcional a L). Sería
conveniente utilizar
d2
I2  
área
Dicha medida vale para uno para un círculo y es menor que uno para el resto de los objetos;
es una medida de la circularidad del objeto. Por ejemplo, para un rectángulo 2xL vale
π/(2L), que nos dice que es inversamente proporcionar a la longitud L del rectángulo.
7. Segmentación de imágenes basada en división de regiones.
Respuesta:
Viene recogida en los apuntes de clase.
8. La modulación delta: Transformación, cuantificación y codificación.
Respuesta:
Viene recogida en los apuntes de clase.
Respuesta a las cuestiones del Examen de
PROCESAMIENTO DE IMÁGENES
18-II-2002
1. ¿Qué transformación puntual utilizarías para aumentar el contraste de la imagen
digital de la figura 1 observando su histograma (figura 2).
Figura 1. Imagen Digital.
Figura 2. Histograma.
Respuesta:
Observando el histograma se tiene obtiene que imagen original tiene su rango de
variabilidad de tonos de gris en el intervalo [100, 240]. En el intervalo [200, 240] se
concentra el mayor número de píxeles; por ello, utilizaríamos la siguiente transformación
de tramos lineales:
0
a( x  100)

T ( x)   255 - 100a
( x  200)  100a

40

255
si
0  x  100
si 100  x  200
si 200  x  240
si 240  x
Tomaríamos a<255/140 para garantiza que la pendiente del primer tramo lineal sea menor
que la del segundo, donde está el mayor número de píxeles (ver la figura 3).
0
100 200 240
Figura 3. Transformación de tramos lineales.
3. Determina la transformada de Fourier discreta de la máscara M=[1/3 1/3 1/3]. ¿Es
un buen filtro de paso baja?
Respuesta:
F (u, v) 
11
(1)u 0v  1 1
0u 0v  1 1
u 0v 



exp  2 i(
 ) 
exp  2 i(  )  
exp  2 i(  ) 
33
3
3  33
3
3  33
3 3 



1
1 1
 exp(2 ui / 3)   exp(2 ui / 3)
9
9 9
1 2
=  cos(2 u / 3)
9 9
Esta función está representada en la figura 4. Como puede observarse la función es
periódica de periodo 3 y simétrica con respecto al origen; se repite la función definida en el
intervalo [-3/2, 3/2]. Como es decreciente en el intervalo [0, 3/2] atenúa más las altas
frecuencias por lo que se trata de un filtro de paso bajotambién deja pasar cientos rangos
de altas frecuencias, que pueden corresponder a cierto tipo de ruido. Nos es un buen filtro
de paso bajo.
1
0.8
0.6
0.4
0.2
0
-0.2
-0.4
-4
-3
-2
-1
0
1
2
3
4
Figura 4. Transformada de Fourier del filtro.
4. Identificación de patrones: ¿Cómo identificarías en una imagen el lugar donde se
encuentra un objeto determinado cuya imagen es bien conocida? (figura 5).
objeto
Figura 5. Imagen ósea.
Figura 6. Mamografía
Respuesta:
Se utiliza una plantilla del tamaño del objeto, cuyos valores son los tonos de gris
correspondientes del objeto en cuestión. Se selecciona el nivel de gris de un pixel central de
dicha plantilla y se recorre la imagen original identificando los píxeles que presentan el
mismo tono de gris que el píxel seleccionado. Sobre cada píxel identificado de la imagen se
superpone la plantilla y se calcula la diferencia entre las matrices correspondientes a dichas
ventanas. Si la matriz resultante es nula, el pixel identificado nos la una posición donde se
encuentra un objeto idéntico al de la plantilla.
6. Detección de un vaso capilar en la mamografía de la figura 6 mediante la transformada
de Hough (se supone que los vasos capilares vienen dados por dos rectas paralelas y que se
pueden encontrar múltiples rectas paralelas por no estar bien definidos).
Respuesta:
Partimos de una imagen binaria de bordes, B(x, y), y del conjunto de píxeles C={(x,y):
b(x,y)=1} que suponemos que tiene P píxeles.
Se trata de identificar el par de restas paralelas más destacado. Se sabe que dos rectas son
paralelas si sus valores del parámetro  son idénticos o, también, si sus valores son o y o
+, siempre que o  [/2, 0], para garantizar que pasen por el primer cuadrante que es el
que contiene la imagen digital. Por lo tanto, podemos utilizar el algoritmo basado en la
transformada de Hough pero con la siguiente modificación: el par de rectas paralelas
corresponde a aquellas dos rectas cuyos contadores C(,1) y C(,2) ó C(,3) y C(
+,4) conduce a un valor máximo de su suma, C(,i) + C(,2) ó C(,3) + C( +,4).
Algoritmo:
Iniciar contadores a cero: C(,) = 0.
Para i =1 a P
Para  =/2 a 
 = xicos+yisen
C(,) = C(,) + 1
fin
fin
Determinar *, 1* y  2* que corresponden al máximo de las dos siguientes cantidades:
Max C ( , 1 )  C ( , 2 ) ó
1 , 2 ,
Max
1 , 2
 [  / 2,0]
C ( , 1 )  C (   , 2 )
7.- ¿Cuál es el efecto de los operadores morfológicos de abertura y cierre sobre los
contornos convexos y sobre los contornos cóncavos de un objeto de la imagen?
Respuesta:
El operador abertura impone la forma de la plantilla sobre las partes convexas de un
contorno y así se puede suavizar el contorno convexo:
Si se utiliza como elemento estructurante una plantilla vertical 31 se suaviza un poco la
parte convexa, como se muestra a continuación:
Operador Abertura
y apenas modifica las partes cóncavas. En cambio, si hubiéramos utilizado como elemento
estructurante una cruz,
el contorno convexo no se altera.
Por otra parte, el operador cierre impone la forma de la plantilla sobre las partes cóncavas
del contorno y así se puede suavizar el contorno cóncavo.
Si se utiliza como elemento estructurante una plantilla vertical 31 se suaviza la parte
cóncava, como se muestra a continuación:
Operador Cierre
y apenas modifica las partes convexas. En cambio, si hubiéramos utilizado como elemento
estructurante una cruz,
el contorno cóncavo no se altera.
NOTA: Las demás cuestiones han sido desarrollas en clase y están recogidas en
los apuntes.
E.T.S.I. Informática
Universidad de Málaga
RESPUESTAS a las cuestiones del
Examen de PROCESAMIENTO DE IMÁGENES / 2-II-2001
1. ¿Cómo deducirías que una imagen binaria tiene ejes a partir de la matriz de
relación espacial?
Respuesta: Un eje vertical, de 45o o de –45o, viene caracterizado porque el pixel de
su izquierda vale cero y el de su derecha uno, o el de su izquierda uno y el de su derecha
cero, como se muestra en las figuras 1(a) y 1(b).
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
(a)
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
1
0
0
1
1
0 1
1 1
1 1
1 1
(b)
1
1
1
1
1
1
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0 0
0 0
1 1
1 1
(c)
0
0
1
1
0
0
1
1
Figura 1. (a) Imagen con una arista vertical. (b) Imagen
con una arista de 45º. (c) Imagen con una arista horizontal.
Si elegimos la relación, (i, j)  (i+1, j), obtenemos una matriz de relación espacial
cuyo elemento (1, 2) nos da el número de pixeles con valor 0 cuyo pixel de la derecha
tiene valor 1, y el elemento (2,1) nos da el número de pixeles que tienen valor 1 y cuyo
pixel de la derecha tiene valor cero. La suma de los valores de dichos elementos de la
matriz nos dan el número total de ejes locales verticales o de 450. Así, la matriz de
relación espacial de la imagen de la figura 1(a) es:
8 4 


 0 12 
En valor 4 del elemento (1, 2) nos indica la presencia de 4 ejes locales según la relación
previamente establecida.
Análogamente, con la matriz de relación espacial basada en la relación, (i, j)  (i, j+1),
los valores de los elementos (1,2) y (2,1) nos determinan el número total de ejes locales
horizontales o de 450. La matriz de relación espacial de la figura 1(c) según dicha
relación es:
7 0


7 7
Por lo tanto, a partir de dicha matriz podemos tener una idea del tamaño de los
contornos de los objetos de la imagen binaria.
2. ¿Qué transformación de tramos lineales utilizaría para mejorar la calidad de la
imagen de la figura 1, teniendo en cuenta su histograma?
Respuesta: Utilizaríamos la curva de tramos lineales que se muestra en la figura 2, que
tiene tramos con pendiente mayor que uno en las zonas del histograma que
corresponden a frecuencias relativas más altas, y pendiente menor que uno en las más
bajas.
Figura 2. Imagen de la luna junto con su histograma.
3. Determina la transformada de Fourier discreta de la máscara M=[1 0 2 0 1]
y analiza sus características. ¿Corresponde a un filtro de paso de banda?
Respuesta: La transformada de Fourier discreta de dicha máscara es la siguiente:
1
H (u, v)  (1) exp( 2i(2)u / 5)  2 exp( 2i(0)u / 5)  (1) exp( 2i(2u / 5))
5
=
2   exp( 4iu / 5)  exp( 4iu / 5) 
1 

5  
2

2
1  cos(4u / 5)
5
Su representación gráfica se muestra en la figura 3. Como se puede observar acentúa
sólo ciertas bandas de frecuencias y atenúa las restantes. Es un filtro de paso banda.
=
Figura 3. Transformada de Fourier discreta
del filtro de paso de banda.
También se puede demostrar, en el dominio espacial, que es un filtro de paso banda,
pues basta con expresarlo como diferencia de un filtro de paso baja con otro de paso
baja (con plantilla de mayor tamaño que el anterior), es decir:
1
1
1
[1 0 2 0 1] = [0 1 2 1 0] 
[1 1 0 1 1].
4
4
4
También se puede expresar como sigue:
1
1
1
[1 0 2 0 1] = [0 1 3 1 0] 
[1 1 1 1 1].
5
5
5
4. ¿Cómo conseguirías una imagen donde apareciera sólo la carretera (línea blanca) de
la figura 1 en un fondo más o menos uniforme?
Respuesta: Aplicamos el operador MIN, con el tamaño apropiado de plantilla (77), a
la imagen de tonos de gris de la figura 5 y conseguimos eliminar la carretera de la
imagen al mismo tiempo que erosionamos las zonas más blancas (como el lago). A
continuación aplicamos el operador MAX para dilatar la imagen obtenida. Finalmente,
restamos a la imagen inicial la imagen que acabamos de obtener. La imagen resultante
contiene la carretera con un fondo más o menos negro.
f(m,n)
f(m,n)
MIN
MAX
RESTAR
fc(m,n)
Figura 4. Proceso de identificación.
Figura 5. Imagen aérea.
5. Deduce el filtro seudoinverso que se utiliza para la restauración de imágenes.
Respuesta: Ha sido desarrollada en clase y viene recogida en los apuntes.
6. Describe la modulación delta para la compresión de imágenes: Transformación,
cuantificación y codificación.
Respuesta: Ha sido desarrollada en clase y viene recogida en los apuntes.
7. La elongación se puede definir como la razón entre la longitud de lado mayor, a, y
la longitud del lado menor, b, de rectángulo de área mínima que contiene al objeto.
b
a
Figura 6. Rectángulo de menor área que contiene a un objeto
¿Qué inconvenientes presenta? ¿Cómo definirías una medida de rectangularidad?
Respuesta: No es una buena media de elongación, pues, por ejemplo, al objeto de la
figura le asigna valor 1, y sin embargo, es un objeto alargado.
Figura 7. Objeto alargado.
Una medida de rectangularidad viene dada por el cociente entre el área del objeto y el
área de rectángulo de menor área que lo contiene, es decir,
=
área de objeto
,
ab
siendo a y b las longitudes de los lados del rectángulo de menor área que contiene a
dicho objeto. Para cualquier rectángulo  siempre vale la unidad y es una medida
normalizada,
01.
8. Aproximaciones poligonales de contornos basadas en el criterio minimax.
Respuesta: Ha sido desarrollada en clase y viene recogida en los apuntes.
RESPUESTAS A LAS CUESTIONES DEL EXAMEN DE
PROCESAMIENTO DE IMÁGENES
DEL DÍA 12-9-2001
1. Por tratarse de ruido granular se utiliza el filtro mediana siguiente:
f*(m,n) = mediana {f(m-1,n-1}, f(m,n), f(m+1,n+1)}
que corresponde a la plantilla
0 0 1
0 1 0
1 0 0
Figura 1. Eliminación del ruido granular.
2. Se puede utilizar la transformación de tramos lineales siguiente (ver la figura 2):
0
si
f (m, n)  r1

255
 255
f * (m, n)  
f (m, n) 
r1
si r1  f (m, n)  r2
r

r
r

r
2
1
2
1


si
f (m, n)  r2
255
f*(m,n)
f(m,n)
r1
r2
Figura 2. Transformación de tramos lineales
Figura 3. Transformación de la imagen
3. Como los bordes (aristas) de una imagen corresponden a las posiciones donde se
produce una transición de valores positivos a valores negativos (o al revés) en la
transformación que corresponde al filtro Laplaciano de la Gaussiana, basta con asignarle el
blanco a los valores positivos y el negro a los negativos. Los contornos de la nueva imagen
binaria nos dan las aristas de la imagen original.
4. La transformada de Fourier discreta de la plantilla [1/3 1/3 1/3] es:
1
exp (2i(1)u / 3  exp (2i0u / 3  exp (2i1u / 3
3
1
exp( 2iu / 3)  exp( 2iu / 3) 
= 1  2

3
2
F(u,v) =
=
1
1  2 cos(2u / 3)
3
La representación gráfica, que se muestra en la figura 3, nos indica que no es un buen filtro
de paso baja, pues sólo atenúa ciertas bandas de alta frecuencia.
Figura 3. Transformada de Fourier discreta del filtro.
5. Viene recogida en los apuntes de clase.
6. Para eliminar el hueco blanco del círculo negro grande (ver la figura 4) se utilizaría el
operador cierre, asignando el valor 1 al objeto, es decir, a los círculos, y el valor 0 al
fondo.
f*(m,n)=(f(m,n)h(m,n)) h(m,n)
siendo h el elemento estructurante
0
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
1
1
1
0
Asimismo, para eliminar los círculos pequeños (del tamaño de la plantilla), se utilizaría el
operador abertura,
f*(m,n)=(f(m,n)  h(m,n)) h(m,n)
Figura4. Esmalte.
7. Viene recogida en los apuntes de clase.
8. Si deseamos detectar todos cuadrados, cuya longitud del lado es l, podemos utilizar la
transformación de Hough. A cada conjunto de píxeles {(xi, yi), iC} que configura un
cuadrado, en la imagen de aristas, cuya longitud de cada uno de sus lados es igual a l, se le
asigna un punto en el espacio de los parámetros (a,b), que corresponde al centro de dicho
cuadrado. A cada píxel se le asigna un cuadrado en el espacio de los parámetros (a,b),
determinado por la ecuación:
Maxx  a , y  b  
y
l
2
b
(xi,yi )
(ao,bo)
(ao,bo)
x
a
Figura 4. Transformación de Hough.
Todos los cuadrados del espacio paramétrico (a,b) correspondientes a los píxeles de los
lados de un cuadrado del espacio (x,y), con centro en (ao,bo) se cortan en el punto (ao,bo). El
contador A(ao,bo,l) nos dirá el número de cuadrados del espacio paramétrico que se cortan
simultáneamente en el punto (ao,bo). Es decir, el número de píxeles que configuran el
cuadrado del espacio cartesiano (x,y) que tiene como centro (ao,bo) y lado l.
Algoritmo:
Paso 0: A(a,b,l)=0, a=a1, a1+1,....,a1+c, b=b1, b1+1,....,b1+d, l=1,2,...,h
Paso 1: Para i=1,2,...,m, j=1,2,…,n
Para a=a1, a1+1,....,a1+c
Para , b=b1, b1+1,....,b1+d
l  2Maxx  a , y  b 
A(a,b,l)=A(a,b,l)+1
fin
fin
fin
Paso 2: Para a=a1, a1+1,....,a1+c
Para b=b1, b1+1,....,b1+d
Para l=1,2,...,h
Si A(a,b,l) umbral entonces
detectamos un cuadrado con centro (a,b) y lado l
fin
fin
fin
Respuestas a las cuestiones del examen de
Procesamiento de Imágenes del día 18-2-2000
1. La transformada de Fourier de la función de interpolación utilizada en el teorema de
Witaker-Shanon viene dada por la expresión:
T T
F (u, v)   1 2
0
para u  u c y v  v c
en otro caso
siendo T11/(2u1) y T21/(2v1).
2. Cuantificadores uniformes: Desarrollado en clase (ver apuntes).
3. La transformada de Fourier de la plantilla [ 1/16 0 1/8 0 1/16 ] es la
siguiente:
1
1
1
1 1
F (u, v) 
exp( 2 2ui)  exp( 2 0ui) 
exp( 2 (2)ui)   cos(4u )
16
8
16
8 8
Su representación gráfica como función de u se puede ver en la figura 1:
Figura 1. Representación gráfica de la transformada de Fourier de la plantilla dada.
Se puede observar que se trata de un filtro de paso de banda que atenúa las bajas
frecuencias y, también, ciertas bandas de alta frecuencia.
Para ver que es un filtro de paso de banda en el dominio espacial expresamos dicha
plantilla como diferencia de dos plantillas de paso baja, una de tamaño 3 y la otra de
tamaño 5:
[ 1/16 0 1/8 0 1/16 ] =
[ 0 1/4
1/2
1/4 0 ]  [ 1/16 1/4 6/16 1/4 1/16 ]
Esta descomposición no es única, otras posibles son:
[ 0 1/8
[ 0 1/16
6/8
14/16
1/8 0 ]  [ 1/16 2/16 10/16 2/16 1/16 ]
1/16 0 ]  [ 1/16 1/16 12/16 1/16 1/16 ]
4. Filtros recursivos: La plantilla equivalente a la aplicación consecutiva de las
plantillas dadas se obtiene de la forma siguiente:
M  1/2f*(i,j) + 1/4f*(i,j+1) + 1/4f*(i,j-1)=
=1/2[1/2f(i,j)+1/4f(i-1,j)+1/4f(i+1,j)] + 1/4[1/2f(i,j+1)+1/4f(i-1,j+1)+1/4f(i+1,j+1)] +
+ 1/4[1/2f(i,j-1)+1/4f(i-1,j-1)+1/4f(i+1,j-1)]
1 / 16 1 / 8 1 / 16
=  1 / 8 1 / 4 1 / 8   f (i, j )
1 / 16 1 / 8 1 / 16
5. Para la identificación de los cuadrados 33 en una imagen binaria utilizaremos el
operador morfológico de aciertos y fallos. Se toman como plantillas
0
0

g 1  0

0
0
0 0 0 0
1 1 1 0
1 1 1 0 ;

1 1 1 0
0 0 0 0
1
1

g 2  1

1
1
1 1 1 1
0 0 0 1
0 0 0 1

0 0 0 1
1 1 1 1
y el centro de dichos cuadrados viene dado por lo pixeles con valor uno en la imagen
binaria siguiente:
b(m,n) = [f(m.n)
g1(m,n) ]  [f (m.n)
g2(m,n) ]
6. Se trata de determinar las dos restas paralelas más destacadas que tomaremos como
modelo para identificar el vaso capilar presente en la mamografía. Para ello utilizamos
la transformada de Hough. Primero se aplica un filtro de paso alta a la imagen original
f(·,·), como puede ser el filtro de Sobel, y a la imagen obtenida se le aplica el operador
umbral, que nos da una imagen binaria donde los pixeles de las aristas más destacadas
valen uno y los demás cero. A continuación detectamos mediante el siguiente algoritmo
las líneas rectas de la imagen de aristas.
1. Partimos de los contadores igualados a cero, es decir,
C(, r ) = 0, para  = 1,...,a, r = r1,...,rb.
2. Para  = 1,...,a hacemos:
Para todos los pixeles (xi, yi) con f(xi, yi)=1 determinamos
r = xi cos  + yi sen 
y ponemos C(, r ) = C(, r ) + 1.
El algoritmo nos da la matriz de contadores C(, r ). Las restas paralelas son aquellas
que tiene un mismo valor de . Sea C(i, r1(i)) el valor máximo de la fila i de dicha
matriz y C(i, r2(i)) el segundo valor mayor de dicha fila. Podemos tomar como vaso
capilar aquellas dos rectas que corresponden al valor h cuya suma
C(i, r1(i)) + C(i, r2(i)).
es máxima.
Es decir, que corresponde a la fila cuya suma de sus dos mayores elementos es máxima.
Fig. 2. Mamografía
7. Detección de aristas: Una vez aplicado un filtro de segundo orden, como el filtro de
Laplace, pasamos a una imagen binaria donde los valores negativos son negros y los
positivos son blancos. Los puntos frontera de esta imagen binaria nos dan las aristas de
la imagen original pues corresponde a los pixeles donde se producen los cambios de
valores positivos a negativos y de negativos a positivos.
1 (blanco)
e(m, n)  
0 (negro)
si f (m, n)  L(m, n)  0
si f (m, n)  L(m, n)  0
Como el filtro de Laplace es muy sensible al ruido es conveniente filtrar previamente la
imagen original con un filtro de paso baja, como puede ser el filtro Gaussiano. De esta
forma se obtiene el filtro LG (Laplaciano de la Gaussiana), que consiste en aplicarle
el filtro Laplaciana a la imagen obtenida después de aplicarle el filtro Gaussiano a la
imagen original.
Saturno
Aristas
Figura 3. Imagen de Saturno.
8. Corrección de la iluminación irregular. Para conseguir la imagen e) con
iluminación uniforma basta dividir la imagen a) por la imagen c). Los pixeles de fondo
tomaran el valor 1, y los pixeles de los objetos tomaran valores mayores que uno si son
más luminosos que el fondo y valores menores que uno si son menos luminosos.
Observando el histograma de la imagen e) sólo tenemos que multiplicar por una
constante para aumentar el brillo, pero la imagen resultante tiene ya iluminación
uniforme y en ella se distinguen perfectamente los diferentes objetos para poder
segmentarla utilizando los mínimos del histograma como valores umbrales. Se obtiene
así dos valores umbrales que nos conducen a tres tipos de objetos: los círculos oscuros,
los círculos claros (que ahora se diferencian mejor del fondo) y el fondo (ver la figura
4).
Figura 4. Corrección de la iluminación irregular.
Málaga, a 22 de marzo de 2000
Fdo. José Muñoz Pérez
Respuesta a las cuestiones del Examen de
PROCESAMIENTO DE IMÁGENES
19-IX-2000
1.- ¿Cómo eliminarías el ruido de la imagen de la figura 1 evitando que los ejes
horizontales queden difuminados?
Figura 1.
Respuesta:
Mediante un filtro mediana horizontal de tamaño 1(2r+1), dado por la expresión:
f*(m,n) = Mediana { f(m-r,n), f(m-r+1,n),...,f(m,n),..., f(m+r-1,n), f(m+r,n) }.
4.- ¿Cómo corregirías el efecto de una iluminación no uniforme en una imagen como
la que aparece en la figura 2?
Figura 2.
Respuesta:
Se aplica el operador MiN, con una ventana de tamaño (2K+1)(2K+1), K15, a la
imagen:
f*(m,n) = MÍNIMO{ f(m-K, n+K), f(m-K-1,n+K),..., f(m,n),..., f(m+K, n-K) }
Esta imagen mantiene el efecto de iluminación no uniforme de la imagen original. Se
resta a la imagen original f(m,n) la imagen f*(m,n). Con ello se consigue una imagen
como la original (un poco más oscura) pero con iluminación uniforme. Para mejorar la
imagen sólo tendríamos que aplicarle un operador de igualación del histograma.
5.- ¿Cuál es el efecto de los operadores morfológicos de abertura y cierre sobre los
contornos convexos y sobre los contornos cóncavos de un objeto de la imagen?
Respuesta:
El operador abertura impone la forma de la plantilla sobre las partes convexas de un
contorno y así se puede suavizar el contorno convexo:
Si se utiliza como elemento estructurante una plantila 33 se suaviza un poco la parte
convexa, como se muestra a continuación:
Operador Abertura
y apenas modifica las partes concavas. En cambio, si hubiéramos utilizado como
elemento estructurante una cruz,
el contorno convexo no se altera.
Por otra parte, el operador cierre impone la forma de la plantilla sobre las partes
cóncavas del contorno y así se puede suavizar el contorno cóncavo.
Si se utiliza como elemento estructurante una plantila 33 se suaviza la parte cóncava,
como se muestra a continuación:
Operador Cierre
y apenas modifica las partes convexas. En cambio, si hubiéramos utilizado como
elemento estructurante una cruz,
el contorno cóncavo no se altera.
7.- Qué información nos da la matriz de relación espacial (co-occurrence matrix)
acerca de la textura? Aplícala a las dos imagen binarias siguientes:
1212
1212
1212
1212
1111
2222
1111
2222
Respuesta:
La matriz de relación espacial permite detectar texturas en una imagen, buscando una
relación entre pixeles adecuada, cuando los elementos positivos de la misma están en
torno a la diagonal principal. Si tomamos la relación (m,n)  (m,n+1) la matriz de
relación espacial de la primera imagen es:
6 0


0 6
que indica la existencia de una textura. Análogamente, para la relación (m,n) (m+1,n)
la matriz de la segunda imagen es la misma que la anterior e indica, por tanto, la
presencia de una textura.
Las respuestas a las preguntas 2, 3, 6 y 8 vienen recogidas en los apuntes de clase.