Page 1 Capítulo 5 / Sección 5.4 11 SOLUCIONES 1. En cada uno
Anuncio
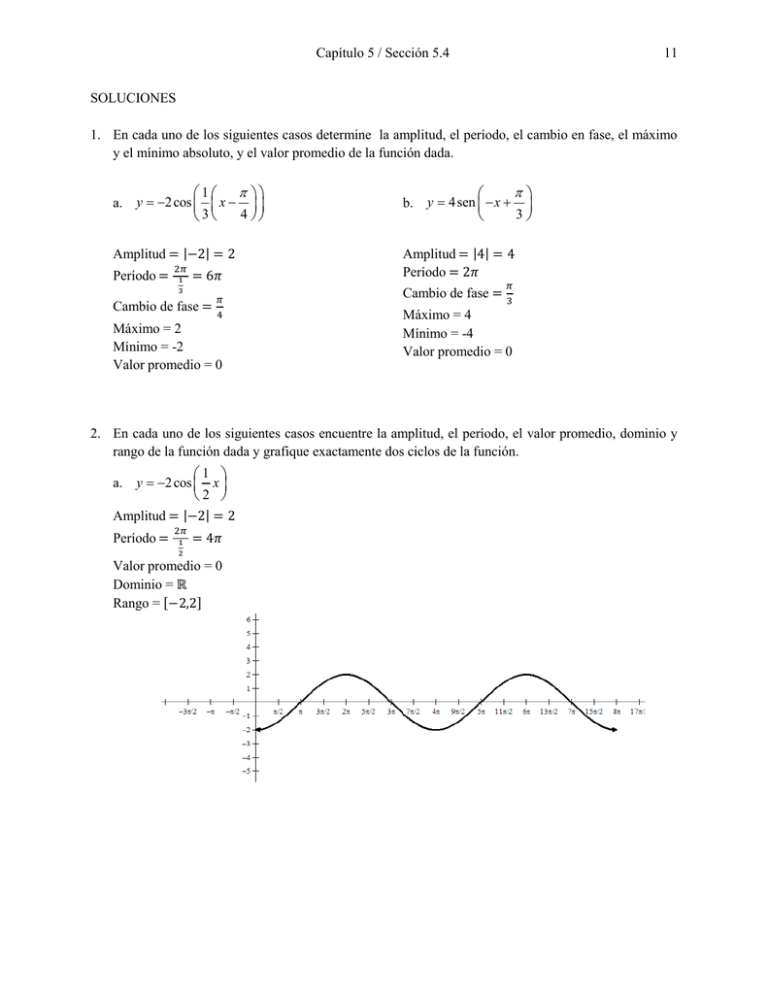
Capítulo 5 / Sección 5.4 11 SOLUCIONES 1. En cada uno de los siguientes casos determine la amplitud, el período, el cambio en fase, el máximo y el mínimo absoluto, y el valor promedio de la función dada. a. 1 y 2 cos x 4 3 Amplitud = |−2| = 2 Período = 2𝜋 1 3 = 6𝜋 Cambio de fase = 𝜋 4 Máximo = 2 Mínimo = -2 Valor promedio = 0 b. y 4 sen x 3 Amplitud = |4| = 4 Período = 2𝜋 𝜋 Cambio de fase = 3 Máximo = 4 Mínimo = -4 Valor promedio = 0 2. En cada uno de los siguientes casos encuentre la amplitud, el período, el valor promedio, dominio y rango de la función dada y grafique exactamente dos ciclos de la función. 1 y 2 cos x 2 Amplitud = |−2| = 2 a. Período = 2𝜋 1 2 = 4𝜋 Valor promedio = 0 Dominio = ℝ Rango = [−2,2] 12 b. 5.4 Gráficas de Seno y Coseno y 3sen 3 x 1 Amplitud = |3| = 3 Período = 2𝜋 3 Valor promedio = -1 Dominio = ℝ Rango = [−4,2] 3. a. Encuentre b tal que la función y 𝑃= 𝜋 8 entonces 𝜋 8 = 2𝜋 𝑏 1 sen bx tenga período 2 por lo tanto 𝑏 = ±16 8 . b. Encuentre b tal que la función y 3cos b x tenga período 2 . 𝑃 = 2𝜋 entonces 2𝜋 = 2𝜋 𝑏 por lo tanto 𝑏 = ±1 Capítulo 5 / Sección 5.4 13 4. Para cada una de las siguientes gráficas encuentre una ecuación de la forma y a sen bx c y también una ecuación de la forma y a cos bx c que le corresponda, donde a 0 , b 0 , y c es lo más pequeño posible en magnitud. Así para cada gráfica se deben hallar dos ecuaciones, una con la función seno y la otra con coseno. a 𝑃=𝜋 𝐴=2 𝜋 )) 12 𝜋 𝑦 = 2𝑐𝑜𝑠 (2 (𝑥 + )) 3 𝑦 = 2𝑠𝑒𝑛 (2 (𝑥 + . b. 𝑃=2 𝐴=3 𝑦 = 3𝑠𝑒𝑛(𝜋𝑥) 1 𝑦 = 3𝑐𝑜𝑠 (𝜋 (𝑥 − )) 2 14 5. 5.4 Gráficas de Seno y Coseno I 120 sen 40 t , t 0 4 ¿Cuál es el período? ¿Cuál es la amplitud? ¿Cuál es el cambio en fase? ¿Cuál es la corriente en 1 t segundos? 20 Grafique dos períodos de esta función. Solución 1 20𝜋 1 Como 𝐼 = 120 sin (40𝜋 (𝑡 − 160)), entonces 𝑃 = 40𝜋 = 20. 1 𝐴 = |120| = 120 y el cambio de fase es 160. 1 1 1 𝐼 ( ) = 120 sin (40𝜋 ( − )) = −60√2 20 20 160 6. Indique donde comienza y donde termina un ciclo completo de la función y cos 5 x 4 . La función se puede reescribir de la forma 𝑦 = −𝑐𝑜𝑠 (5 (𝑥 + cambio de fase es 4𝜋 − 5. Un ciclo completo empieza en − 4𝜋 5 y termina en − 2𝜋 . 5 4𝜋 )) 5 por lo tanto el período es 2𝜋 5 y el











