Péndulo de Kater
Anuncio

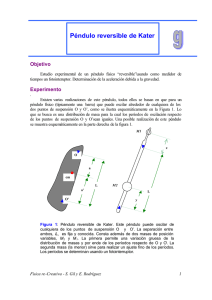
Péndulo de Kater • Introducción teórica El período de un péndulo físico de masa m que oscila alrededor de su centro de suspensión O, viene dado por: Siendo I el momento de inercia del péndulo respecto al eje de oscilación que pasa por O, y h la distancia desde O al centro de masas del cuerpo, G. El centro de masas es el punto del cuerpo tal que cuando estudio ese sistema, lo trato como un punto con masa = masa total del sistema situado en el centro de masas. Un péndulo reversible es aquel que puede oscilar alrededor de 2 centros de suspensión, O1 y O2, con sus respectivos períodos T1 , T2 y siendo h1 , h2 las distancias desde O1, O2 a G. Péndulo reversible Entonces tenemos: 1 Y por el teorema de Steiner: Sustituyendo I1 e I2 en T1 y T2 llegamos a la relación: De la que podemos despejar g si conocemos h1, h2, T1 y T2. Determinar g es el objetivo de la práctica. • Dispositivo experimental −Un péndulo reversible con los 2 centros de suspensión ajustables a distintas distancias del centro del péndulo. Esto era gracias a unos ajustadores, que funcionaban apretando y desapretando los centros de oscilación con una tuerca. −2 cronómetros con precisión de 1e−2 s −Una barra delgada de unos 0,1 m de largo que salía de la mesa de trabajo paralela al suelo. −Una regla con precisión de 1e−3 m • Método experimental Para hallar h1 y h2, fijamos a una distancia arbitraria los centros de suspensión, y colocamos el péndulo en la barra delgada como indica la figura de arriba. Movemos el péndulo hacia los lados hasta que alcanza el reposo. El punto sobre el que alcanza el reposo es el centro de masas, G (figura de arriba). Ahora podemos medir h1 y h2 con la regla. (h1: distancia desde el centro de masas al centro de suspensión O1). Para hallar T1 y T2, hacemos oscilar el péndulo apoyado en O1. Contamos con el cronómetro el tiempo empleado en hacer 20 oscilaciones. Dividimos esta cantidad entre 20 y nos da T1. Análogo para T2. Como para hallar g necesitamos h1^2 − h2^2 y T1^2*h1 − T2^2*h2 , deberemos fijarnos en que si variamos h1 y h2 de manera que h1^2 − h2^2 tenga valores parecidos, los nuevos datos no nos aportarán demasiada información. Por eso, nosotros sólo variábamos uno de los fijadores. • Datos experimentales h1 h2 h1^2−h2^2 T1 0,767 0,708 0,08702+−3.8e−4 2,1838+−3.0e−3 T2 T1^2*h1 − T2^2*h2 gravedad 2,1579 +− 6.0e−3 0,361 +− 2.1e−2 9,52 2 2,1289 +− 3.7e−3 2,0745 +− 0,806 0,67 0,20074+−3.9e−4 2,1500+−3.1e−3 3.6e−3 2,0248 +− 0,836 0,627 0,30577+−4.0e−4 2,153+−2.0e−2 3.3e−3 1,9728 +− 0,874 0,606 0,39664+−4.2e−4 2,148+−2.4e−2 3.0e−3 1,9582 +− 0,892 0,59 0,44756+−4.3e−4 2,1242+−8.9e−3 7.0e−3 1,9295 +− 0,918 0,565 0,52350+−4.5e−4 2,1380+−7.0e−3 5.5e−3 La incertidumbre de h1 y h2 es: 2,9e−4 m 0,78 0,7 0,11840+−3.9e−4 2,1669+−9.2e−3 0,490i ± 3.3e−2 9,54 0,842 ± 1.5e−2 9,41 1,303 ± 7.3e−2 9,26 1,674 ± 9.0e−2 9,35 1,763 ± 3.7e−2 10,02 2,0927 ± 3.0e−2 9,88 y = −0,0082+ 0,2507x S(a) = 0,0096 S(b) = 0,0070 R = 0,99803 R^2 = 0,99606 De deducimos que la pendiente de esta recta será igual a => g = 9,90 +− 0.28 Incertidumbres 3 Gravedad: = 0,276348 ... Período: Estimé como valor del período el valor medio de los períodos obtenidos en las distintas mediciones. /*El cinco viene del número de mediciones.*/ La incertidumbre de tipo a (referente a las medidas) es: = Sa(T) = Incertidumbre de tipo a Por tener el cronómetro un precisión de 0,001 s , la incertidumbre de tipo b es: Y la incertidumbre combinada queda: Longitudes: Las mediciones de longitud solo las realizábamos 1 vez por lo que solo tienen incertidumbre de tipo b 4