Trabajo de Investigación Cuerpos Geométricos

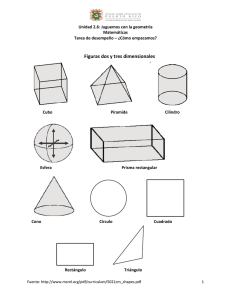
Saint George’s College
Área de Matemáticas y sus Aplicaciones
Tercera Unidad
Trabajo de Investigación
Cuerpos Geométricos
Integrantes:
-Stefan Jercic
-Ignacio Larrain
-Cristian Majluf
Curso:
10°E
Profesora:
Marta Joignant
Fecha de entrega:
29 de octubre de 1999
CUERPOS GEOMÉTRICOS
1. Clasifique los cuerpos geométricos.
Dos grupos de sólidos geométricos del espacio presentan especial
interés:
1.1. Poliedros: Aquellos cuerpos geométricos totalmente limitados
por polígonos, como por ejemplo, el prisma, la pirámide; etc.
1.2. Cuerpos redondos: aquellos cuerpos geométricos
engendrados por la rotación de una figura plana alrededor de su
eje, como la esfera, el cilindro, etc.
2. Clasifique los poliedros.
Algunos poliedros reciben nombres especiales en función del
número de caras que poseen.
Así, se llama tetraedro a todo poliedro de cuatro caras;
pentaedro, al poliedro de cinco caras; hexaedro, al poliedro de seis
caras; heptaedro al de siete caras; octaedro, al de ocho; eneaedro,
al poliedro de nueve caras; decaedro, al de diez caras; endecaedro,
al de once, dodecaedro, al poliedro de doce caras; pentadecaedro,
al de quince caras, e icosaedro, al poliedro de veinte caras.
Los demás poliedros no reciben ningún nombre en particular;
así por ejemplo, se habla de un poliedro de 17 caras, de 22 caras,
etcétera.
Conviene no confundir los poliedros (cuerpos geométricos
cerrados) de los ángulos poliedros correspondientes, a pesar del
gran parecido en las denominaciones de unos y otros, que
únicamente se diferencian en la palabra “ángulo” que figura
antepuesta cuando se trata de un ángulo poliedro y no figura
cuando se trata del poliedro correspondiente.
En el caso del ángulo triedro resulta indiferente la
denominación “ángulo triedro” o la denominación “triedro”, ya que
por no existir el poliedro de tres lados no es posible que se dé la
confusión anterior.
Se entiende por desarrollo de poliedro a la figura obtenida
cuando se representan todas las caras del poliedro sobre un plano,
de manera que cada cara del poliedro aparezca. Unida a sus
adyacentes según la misma arista con la que lo estaba el poliedro.
Se dice que un poliedro es convexo cuando cualquier recta
puede cortar su superficie en dos puntos, lo que equivale a decir
que el poliedro no tiene ningún diedro entrante. En el caso contrario,
es decir, cuando alguna recta corta la superficie del poliedro en más
de dos puntos, se dice que el poliedro es cóncavo. En este caso,
como sé comprende fácilmente, el poliedro tiene algún ángulo
diedro entrante.
Atendiendo a la regularidad de sus elementos se puede
establecer otra clasificación de los poliedros en:
1) Poliedros Regulares. Cuando todas sus caras son
polígonos regulares entre sí y todos sus ángulos diedros y poliedros
son también iguales. Como se verá más tarde, existen únicamente
cinco poliedros regulares.
2) Poliedros Irregulares. Cuando no son regulares, por no
cumplirse algunas o todas las condiciones precisas para ello.
Dentro de los poliedros existen tres grupos importantes: los
prismas, los paralelepípedos y las pirámides.
3. Clasifique los cuerpos redondos.
Los cuerpos redondos son todos aquellos cuerpos o sólidos
geométricos formados por regiones curvas o regiones planas y
curvas.
Un cuerpo redondo se puede definir también como aquel
volumen generado por la revolución de una determinada figura
geométrica en torno a un eje imaginaria.
De ahí que a esta figura imaginaria del espacio también se le
denomina cuerpo de revolución.
Los principales cuerpos redondos son: el cilindro, el cono, y la
esfera.
Los cuerpos redondos son:
• Cilindros
• Conos
• Esferas
Poliedros
4. Arista de un poliedro.
Son los lados de las caras del poliedro.
5. Vértice de un poliedro.
Es la intersección de tres o más de sus aristas.
6. Diagonal de un poliedro.
Son los segmentos que unen dos vértices no pertenecientes a
la misma cara.
7. Dibujo de un poliedro con una de sus diagonales.
7. Seis poliedros regulares y sus dibujos correspondientes.
(Son sólo 5 poliedros regulares)
PRISMAS
9. Defina prisma.
Se denomina prismas aquellos poliedros limitados por dos
polígonos cualesquiera iguales y de dos lados paralelos llamados
“bases” y por tantos paralelogramos como lados tienen las bases.
Dichos paralelogramos reciben el nombre de caras laterales
del prisma.
La distancia entre las dos bases se llama altura del prisma.
Los lados de las bases constituyen las aristas básicas y los
lados de las caras laterales, las aristas laterales, iguales y paralelas
entre sí.
Sección recta de un prisma es el polígono obtenido al cortar
dicho prisma por un plano perpendicular a las aristas laterales.
Tronco de prima es la porción de prisma comprendida entre
una de las bases y una sección recta del prisma no paralela a las
bases.
Atendiendo al número de caras laterales del prisma, los
prismas se clasifican en triangulares (cuando tienes tres caras
laterales), cuadrangulares (si tienen cuatro), pentagonales,
hexagonales, etc.
Atendiendo a la perpendicular entre las bases y las caras
laterales del prisma, un prisma puede ser recto, cuando las aristas
laterales son perpendiculares a las bases; oblicuo, cuando no se
cumplen las condiciones para que sea recto.
Atendiendo a la regularidad de sus bases y al carácter de
recto u oblicuo del prisma, los prismas se clasifican en: regulares,
cuando son rectos y además las bases son polígonos regulares, e
irregulares, caso de que no reúnan las condiciones anteriores.
10. Dibuje un prisma recto y uno oblicuo.
11. Definición área lateral de un prisma
Se entiende por área lateral de un prisma a la suma de las
áreas de las caras laterales del mismo.
El área lateral se obtiene, cuando se trata de un prisma recto,
multiplicando el perímetro de la base por la altura del prisma.
Área lateral del prisma recto = p * a
Si se trata de un prisma oblicuo, el área lateral del prisma se
obtiene multiplicando el perímetro de la sección recta por la arista
lateral del prisma.
Área lateral del prisma oblicuo = pr * a
12. Definición área total del prisma
El área total de un prisma se obtiene sumando al área lateral y
el área de las dos bases
Área total del prisma = p * a + 2B
p: perímetro de la base o bien perímetro de la sección
recta, cuando se trate de un prisma oblicuo;
a: altura, o bien arista lateral, cuando el prisma sea oblicuo;
B: el área de una de las bases del prisma
CUBO
13. Defina y dibuje un cubo.
Es un paralelepípedo cuyas seis caras son cuadradas.
Se trata además de un poliedro regular, ya que todos los
ángulos poliedros son también iguales.
Es un poliedro regular de 6 caras. Se le denomina Hexaedro
(hexa = 6, edro = caras)
14. Dibuje la red de un cubo.
15. ¿Qué es el área lateral de un cubo y cómo se calcula?
• El área lateral de un cubo es igual a la suma de las áreas de las
caras laterales de un cubo.
Se obtiene elevando al cuadrado la arista y el producto de eso se
multiplica por 4.
A = arista
área lateral = A² x 4
16. ¿Qué es el área total de un cubo y cómo se calcula?
El área total de un cubo es igual a la suma del área lateral y el
área de las regiones básales.
Se obtiene elevando al cuadrado la arista y el producto de eso se
multiplica por 2. A todo eso se le suma el área lateral antes
mencionada.
A = arista
área total = A² x 2 + área lateral.
17. ¿Qué es el volumen del cubo y cómo se calcula?
El volumen de un cubo es la medida del espacio que ocupa.
Se obtiene elevando al cubo la arista del cubo.
V = A³
A = arista
18. Con lo investigado resuelva:
a) Calcule el área total de un cubo de arista 6 cm.
6 x 6 = 36cm² = área de cara.
36 x 6 = 216 cm² = área total del cubo.
b) Calcule el área basal de un cubo de arista 17 cm.
17 x 17 = 289cm² = área de cara
289 x 2 = 578cm2 = área basal.
c) ¿Cuánto mide la arista de un cubo si su área total es
150cm²?
156 : 6 = 25cm² = área de cara
¶25 = 5cm = arista.
d) Calcule el volumen de un cubo de arista 6 cm.
6 x 6x 6 = 216cm² = volumen del cubo.
e) Calcule la arista de un cubo si su volumen es 343 cm².
³¶343 = 7cm = arista.
19. Defina y dibuje un paralelepípedo
Se denomina paralelepípedos a aquellos prismas cuyas bases
son paralelogramos como por ejemplo una caja de cerillas, un dado,
etc.
Se comprende fácilmente que un paralelepípedo tiene seis
caras (2 correspondientes a las bases que son paralelogramos y 2 a
las caras laterales).
20. Con lo investigado resuelva.
a) Calcule el área total de un prisma recto cuya base es un
cuadrado cuya arista basal mide 8 cm y la arista lateral 20
cm.
8 x 8 = 64cm² = área cara basal
64 x 2 = 128cm² = área basal
20 x 8 = 160cm² = área cara lateral
160 x 4 = 640cm²= área lateral
128 + 640 = 768 cm² = área total del prisma
b) Calcule el área total de un paralelepípedo que tiene 16 cm
de largo, 8 cm de ancho
y 3 cm de alto.
8 x 3 = 24cm²= área arista basal
24 x 2 = 48cm² = área basal
16 x 3 x 2 = 96cm² = parte de área lateral
16 x 8 x 2 = 256cm² = parte de área lateral
256 + 96 = 352cm² = área lateral.
48 + 352 = 400cm² = área total del paralelepípedo
PIRÁMIDE
21. Defina pirámide.
Se denomina pirámides a aquellos poliedros limitados por un
polígono cualquiera llamado “base” y por tantos triángulos como
lados tiene la base que concurren a un vértice común, llamado
cúspide o vértice de la pirámide.
Las pirámides se pueden clasificar según la región poligonal
que tienen por base y según si esta es regular o no regular.
Además, toda pirámide puede ser recta u oblicua, según el pie de
su altura coincida o no con el centro de su región basal.
22. Defina cada uno de los elementos de una pirámide.
Vértice:
Es el punto donde convergen todos los triángulos que
componen las caras de la pirámide.
Apotema: Es la altura de cada uno de los triángulos que componen
las caras de la pirámide.
Altura: Es la perpendicular que baja desde la cúspide de la
pirámide.
23. Dibuje 4 pirámides que tengan bases distintas y al menos
una de ellas sea oblicua.
24. Defina área lateral de una pirámide.
Se denomina área lateral de una pirámide a la suma de las
áreas de las caras laterales de la misma
El área lateral de una pirámide regular se obtiene hallando la
mitad del producto del perímetro de la base por la apotema de la
pirámide.
25. Defina área total de una pirámide
El área total de una pirámide es igual a la suma del área lateral y
el área basal de una pirámide.
26. N/A
27. ¿Cómo se calcula el volumen de una pirámide?
Se calcula multiplicando la arista basal por la altura y el resultado
de eso se divide en tres.
V (pirámide) = 1/3 Ab x h
altura.
Ab = arista basal
y h=
28. Calcula:
a) El área lateral de una pirámide de base cuadrada de arista
basal 12 cm y su altura es de 16 cm.
(12 x 16) : 2
=192 : 2 = 96cm² = área de cara lateral
96 x 4 = 384cm² = área lateral
b) El área total de una pirámide de base cuadrada si su arista
basal es de 6 cm y la altura es de 4 cm.
6 x 6 = 36 cm² = área basal
(6 x 4) : 2
=24 : 2 = 12
12 x 4 = 48cm² = área lateral
36 + 48 = 84cm² = área total de la pirámide.
c) El volumen de la pirámide anterior.
(6 : 3) x 4
= 2 x 4 = 8 cm³
CUERPOS REDONDOS
29. Defina cuerpo redondo.
Son todos aquellos cuerpos o sólidos geométricos formados por
regiones curvas o regiones curvas y planas. También se puede
definir como aquel volumen generado por la revolución de una
determinada figura geométrica en torno a un eje imaginario
(cuerpos de revolución).
30. ¿Cuáles son los principales cuerpos redondos?
Los principales son el cilindro, el cono y la esfera.
31. Defina cada uno de ellos y dibújelos.
Cilindro: Un cilindro circular recto es aquel cuerpo o sólido
geométrico generado por la revolución de una región rectangular
en torno a uno de sus lados o también en torno a uno de sus ejes
de simetría.
Cono: Un cono circular recto es aquel cuerpo o sólido
geométrico generado por la revolución de una región triangular
en torno a uno de sus catetos o en torno a su eje de simetría.
Esfera: es aquel cuerpo o sólido geométrico generado por la
revolución de un semicírculo en torno a su diámetro.
32. Dibuja la red del cilindro recto y del cono recto.
Cilindro
33. ¿Cómo se calcula el área total de un cilindro?
Si “abrimos” un cilindro recto a lo largo de una generatriz, y lo
extendemos en un plano, obtenemos dos círculos y una región
rectangular. De esta manera se obtiene la red del cilindro recto.
CD: radio
AD: generatriz
BC: altura
BC: eje
A partir de ella podemos ver que el área lateral de cilindro
esta determinada por el área de la región rectangular, cuyo largo
corresponde a su perímetro basal, es decir a 2πr, y cuyo ancho
es la medida de la altura del cilindro, o sea h.
Ál (cilindro) = 2πr •
h
Si a la expresión anterior le sumamos el área de las dos
regiones circulares básales, obtenemos el área total del
cilindro.
Át = Ál + πr² + πr²
Entonces,
Át = 2πrh + 2πr²
Por lo tanto:
Át (cilindro) = 2πr ( h
+r)
(Sé factoriza)
-Ejemplo: Un cilindro recto tiene un radio basal de 4cm y su altura
mide el doble del diámetro de esa base. Calculemos el área total
del cilindro.
Se sabe que: r = 4cm y h = 2 • (diámetro) = 2 • 8cm = 16cm
Át (cilindro) = 2π • 4cm(16cm + 4cm) = 8πcm(20cm) =
160πcm²
34. ¿Cómo se calcula el volumen de un cilindro?
Como hemos visto, podemos considerar un cilindro como un
prisma que tiene por base una región poligonal de lados
infinitamente pequeños.
Por lo tanto, también para un cilindro circular, su volumen es
igual al producto del área del circulo basal por su altura.
Es decir: V (cilindro) = Áb • h
V (cilindro) = πr²
•h
-Ejemplo: El volumen de un cilindro circular cuyo radio basal es de
6cm y cuya altura mide 8cm, es:
V (cilindro) = π(6cm)² • 8cm ≈ 288πcm³ ≈ 904,78cm³
35. Calcule:
a) el área total de un cilindro si su radio basal mide 10cm y su
altura mide 20cm.
Se sabe que: r = 10cm y h = 20cm
2π • 10cm(20cm+10cm) = 20πcm(30cm) = 600πcm²
Át (cilindro) = 600πcm²
b) el volumen del cilindro anterior.
Se sabe que: r = 10cm y h = 20cm
π (10cm)² • 20cm ≈ 2000πcm³ ≈ 6283cm³
V (cilindro) = 6283cm³
c) si el volumen de un cilindro recto es 144πcm³. Si el diámetro
de su región basal mide 12cm, ¿cuál es su área total?
Se sabe que: r = 12cm y h = incógnita
π (12cm)² • h = 144πcm³
144πcm² • h = 144πcm³
h = 144πcm³
144πcm²
h = 1cm
2π • 12cm(1cm+12cm) = 24πcm(13cm) = 312πcm²
Át (cilindro) = 312πcm²
Cono
36. ¿Qué es la generatriz de un cono?
Es una línea lateral imaginaria que es por donde se abre el cono
para quedar como el manto.
37. ¿Qué es el manto de un cono?
• Es la figura “abierta” que representa el área lateral del cono.
38. ¿Cómo se calcula el área lateral de un cono?
Se puede deducir la siguiente porción:
Área sector circular = Longitud arco sector circular
Área círculo
Longitud de la circunferencia
Es decir:
Ál = 2πr Ál = πrg²
(g: generatriz)
πg² 2πg
g
Ál (cilindro) = πrg
Existe otra relación para calcular el área lateral del cono en
función de su altura.
Esto es:
El área lateral de un cono es igual al
producto de su altura por el perímetro del
circulo cuyo radio es la medida del
segmento perpendicular a la generatriz en
su punto medio.
Ál = 2π • ED • h
39. ¿Cómo se calcula el área total de un cono?
Luego si al área lateral del cono le sumamos el área basal,
obtenemos el área total: Át (cono) = πrg + πr²
Át (cono) = πr (g
+ r)
40. ¿Cómo se calcula el volumen de un cono?
• Si consideramos al cono como una pirámide regular cuya base
es una región poligonal de lados infinitamente pequeños,
entonces se tiene que el volumen de un cono es igual al volumen
de una pirámide regular, donde el área basal (Áb) se confunde
con el área de una región circular (πr²).
Sabemos que:
V (pirámide) = 2 Áb • h
Por lo tanto:
V (cono) = V (pirámide) = 2 πr² • h
V (cono) = 2 πr² • h
41. Calcula:
a)el área lateral de un cono recto cuya generatriz mide 9cm y
cuya altura mide lo mismo que el diámetro basal.
Se sabe que: g = 9cm y 2r = h
x² + (2x)² = 81cm
x² + 4x² = 81cm
5x² = 81cm
x² = 81cm
5
x² = ¶16,2 cm
x = 4,02 cm
Ál (cono) = 3,1416 • 4,02cm • 8,04cm
Ál (cono) = 101,5 cm²
b) ¿Cuál es el área lateral de un cono recto cuya región basal
tiene 25πcm² y su altura es de 12cm?
Se sabe que: h = 12cm y que Áb = 25πcm²
Áb (cono) = πr²
πr² = 25πcm²
r² = 25cm²
r = ¶25cm²
r = 5cm
(5cm)² + (12cm)² = x²
25cm² + 144cm² = x²
169cm² = x²
169cm² = x
13cm = x
g = 13cm
Ál (cono) = πrg
πrg = 3,1416 • 5cm • 13cm
πrg = 204,20cm²
Ál (cono) = 204,20cm²
c) Las papas fritas tienen el mismo precio si se entregan en un
envase cónico o en uno rectangular. El cono tiene un radio de
6cm y una altura de 15cm, y las medidas del envase rectangular
son 8cm de ancho, 6cm de alto y 9cm de largo. ¿Cuál de los dos
envases trae mas papas fritas?
(Cono) Se sabe que: r = 6cm y que h = 15cm
V (cono) = π • r² • h
3
π • r² • h = 3,1416 • (6cm)² • 15cm
3
3
π • r² • h = 1696,4cm³
3
3
π • r² • h = 565,4cm³
V (cono) = 565,4cm³
(Rectángulo) Se sabe que: a = 8cm, b = 9cm y c = 6cm
V (rectángulo) = a • b • c
a • b • c = 8cm • 9cm • 6cm
a • b • c = 432cm³
V (rectángulo) = 432cm³
Respuesta: El envase que trae más papas fritas es el cónico.
ESFERA
42. ¿Cómo se calcula el área de una esfera?
El área de la superficie esférica se obtiene multiplicando por 4
el área de un círculo máximo de la esfera.
Superficie esférica = 4πR2
43. ¿Cómo se calcula el volumen de una esfera?
El volumen de la esfera se obtiene hallando los cuatro tercios
del producto del número π por el cubo del radio de la esfera.
Volumen de la esfera = 4/3 π * R3
44. Calcula:
a) El área de una esfera de radio 6 cm.
4 * π * 62 = 452,3897421 cm3
b) El área de una esfera que se encuentra inscrita en un
cubo de arista de 60 cm.
4 * π * (60/2)2 = 11.309,73355 cm3
c) La superficie total y volumen de la Tierra si el radio es
aproximadamente de 6.370 km.
4 * π * 6.3702 = 509.904.363,8 cm3
45. Haga un esquema con la clasificación de los cuerpos en
general.
•
•
•
•
•
Poliedros
regulares
Tetraedro
Hexaedro
Octaedro
Dodecaedro
Icosaedro
Poliedros no
regulares
• Prismas
• Pirámides
• Otros en
General
Cuerpos
redondos
• Cilindros
• Conos
• Esferas