Agrupaciones planas
Anuncio
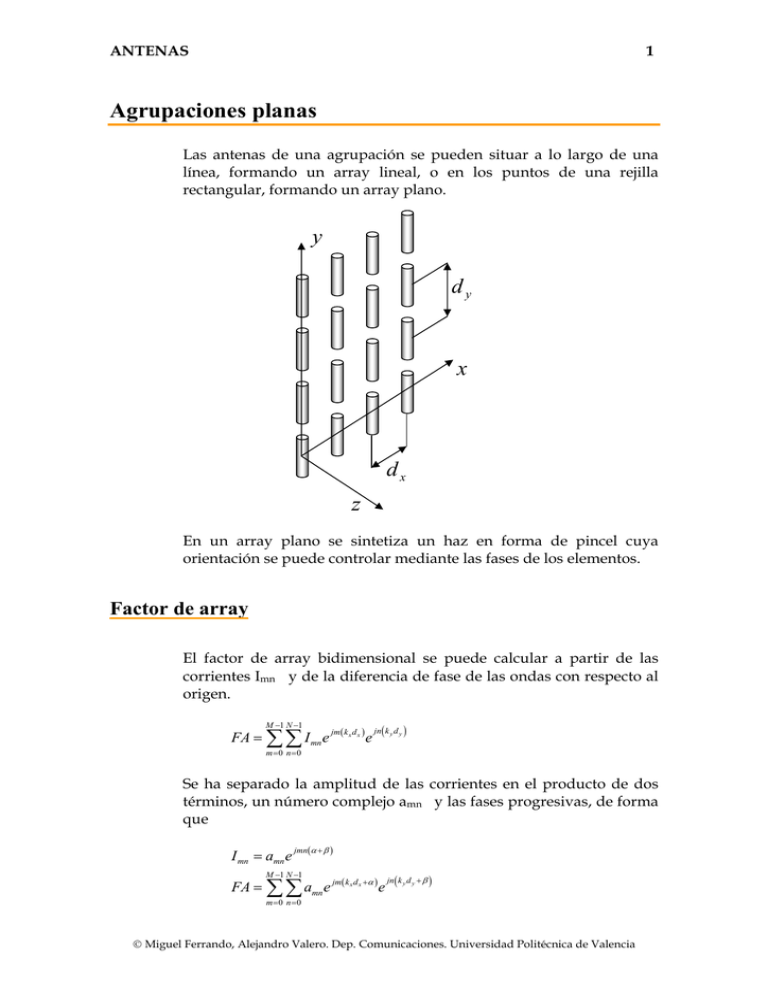
ANTENAS 1 Agrupaciones planas Las antenas de una agrupación se pueden situar a lo largo de una línea, formando un array lineal, o en los puntos de una rejilla rectangular, formando un array plano. y dy x dx z En un array plano se sintetiza un haz en forma de pincel cuya orientación se puede controlar mediante las fases de los elementos. Factor de array El factor de array bidimensional se puede calcular a partir de las corrientes Imn y de la diferencia de fase de las ondas con respecto al origen. M −1 N −1 FA = ∑ ∑ I mn e jm( k x d x ) e ( jn k y d y ) m=0 n=0 Se ha separado la amplitud de las corrientes en el producto de dos términos, un número complejo amn y las fases progresivas, de forma que I mn = amn e jmn(α + β ) M −1 N −1 FA = ∑ ∑ amn e jm( k x d x +α ) e ( jn k y d y + β ) m =0 n =0 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 2 Si la iluminación es separable, es decir que si cada corriente se puede escribir como el producto de dos corrientes entonces el factor de array también se puede escribir como el producto de dos factores. amn e j ( mα + n β ) = bm e M −1 N −1 FA = ∑ ∑ amn e j ( mα ) cn e jm ( k x d x +α ) j ( nβ ) e ( jn k y d y + β m=0 n=0 ) M −1 = ∑ bm e m=0 jm( k x d x +α ) N −1 ∑c e n=0 ( jn k y d y + β ) n Los ángulos eléctricos se definen como ψ x = k x d x + α = kd x sin θ cos φ + α ψ y = k y d y + β = kd y sin θ sin φ + β En un array plano interesa poder apuntar con el haz a una dirección determinada. Las fases progresivas se pueden determinar como α = − kd sin θ 0 cos φ0 β = − kd sin θ 0 sin φ0 Resolviendo ambas ecuaciones se obtienen los ángulos orientación del haz en función de los desfases progresivos. tan φ0 = de β dx αdy 2 ⎛ α ⎞ ⎛ β ⎞ sin θ 0 = ⎜ ⎟⎟ ⎟ + ⎜⎜ ⎝ kd x ⎠ ⎝ kd y ⎠ 2 2 Polinomio de agrupaciones planas Se puede definir un polinomio bidimensional de la agrupación, a partir de las variables complejas (z,w). z = e jψ x w=e jψ y El análisis es similar a las agrupaciones lineales. Se pueden tener agrupaciones con polinomios uniformes, triangulares, binómicos o con coeficientes arbitrarios. En general el polinomio de la agrupación será de la forma © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 3 M −1 N −1 p( z , w) = ∑ ∑ amn z m wn m =0 n =0 En algunos casos particulares se puede escribir como el producto de dos polinomios, esto sucede cuando los coeficientes cumplen la condición amn = bm cn En ese caso el polinomio resultante es M −1 N −1 M −1 N −1 m=0 n=0 m =0 n =0 p ( z , w) = ∑ ∑ amn z m wn = ∑ bm z m ∑ cn wn = p2 ( z ) p3 ( w ) Por ejemplo la agrupación de 3x3 antenas, con corrientes definidas por la matriz ⎡1 2 1⎤ ⎢1 4 1⎥ ⎢ ⎥ ⎢⎣1 2 1⎥⎦ Tendría un polinomio equivalente p ( z , w) = 1 + 2 z + z 2 + w + 4 zw + z 2 w + w2 + 2w2 z + w2 z 2 Esta distribución no sería separable, pero en cambio la distribución ⎡1 2 1 ⎤ ⎢ 2 4 2⎥ ⎢ ⎥ ⎢⎣ 1 2 1 ⎥⎦ Cuyo polinomio equivalente es p ( z , w) = 1 + 2 z + z 2 + 2w + 4 zw + 2 z 2 w + w2 + 2w2 z + w2 z 2 Se puede separar en el producto de dos distribuciones triangulares p( z, w) = (1 + 2 z + z 2 )(1 + 2 w + w2 ) © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 4 Agrupaciones planas uniformes En las agrupaciones planas uniformes, todas las corrientes de las antenas son iguales. El factor de array se puede calcular como amn = 1 M −1 N −1 FA = ∑ ∑ e jm ( k x d x +α ) e ( jn k y d y + β m =0 n =0 ) M −1 = ∑e jm( k x d x +α ) m=0 N −1 ∑e ( jn k y d y + β ) n=0 La agrupación es separable, por lo tanto el factor de array bidimensional es equivalente al producto de los factores de la agrupación lineales de dimensiones N y M ⎛ Mψ x ⎞ sin ⎛ Nψ y ⎞ sin ⎜ ⎜ ⎟ ⎟ ⎝ 2 ⎠ ⎝ 2 ⎠ FA = FAx FAy = ⎛ψ ⎞ ⎛ψ ⎞ sin ⎜ x ⎟ sin ⎜ y ⎟ ⎝ 2 ⎠ ⎝ 2 ⎠ La representación gráfica del FA se puede realizar en forma de superficies o de curvas de nivel. Se muestra el caso de una agrupación uniforme de 3x5 antenas con espaciado λ/2. ψy ψx Asimismo se puede escribir un polinomio bidimensional de la agrupación. M −1 N −1 M −1 N −1 m =0 n =0 m=0 n=0 p ( z , w) = ∑ ∑ z m wn = ∑ z m ∑ wn = p2 ( z ) p3 ( w ) = z M − 1 wN − 1 z −1 w −1 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 5 Diagramas de radiación de agrupaciones planas uniformes En las siguientes gráficas se muestran varios ejemplos de agrupaciones planas de MxN antenas. Las antenas se alimentan en fase y el espaciado es de λ/2. Se puede observar que aumentado el número de antenas mejora la directividad. Con agrupaciones cuadradas el haz es de tipo pincel, mientras que las agrupaciones rectangulares tienen diagramas tipo abanico. M N=2 N=3 N=4 2 3 4 Tabla comparativa de agrupaciones planas de MxN antenas. El espaciado es d x = λ / 2 d y = λ / 2 . Los desfases son α = β = 0 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 6 Agrupaciones planas controladas por fase La agrupación plana con fase constante tiene el máximo en la dirección perpendicular . Modificando la fase progresiva α (distribución según x) se consigue modificar la orientación del haz en el plano XZ, la modificación de la fase β (distribución según y) se cambia la orientación en el plano YZ. Variando ambas fases se consiguen orientaciones arbitrarias. En la figura se muestran varios casos de cambio de orientación, para una agrupación uniforme de 4x4 antenas cuyo diagrama individual es tipo cardidoide. El espaciado entre los elementos es λ/2. α =0 α = −π / 4 α = −π / 2 α =0 α =π /4 α =π /2 © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 7 Margen visible en agrupaciones planas Las ecuaciones que relacionan los ángulos del espacio con los del factor de la agrupación son ψ x = k x d x + α = kd x sin θ cos φ + α ψ y = k y d y + β = kd y sin θ sin φ + β Los márgenes visibles son ψ x ∈ [ −kd x + α , kd x + α ] ψ y ∈ ⎡⎣ −kd y + β , kd y + β ⎤⎦ Ambos valores están relacionados entre sí, de forma que el límite del margen visible no es un rectángulo. ψ x −α = cos φ kd x sin θ ψy −β = sin φ dk y sin θ La ecuación resultante es una superficie elíptica, centrada en α,β y de semiejes kdx, kdy. El límite es una elipse cuya ecuación es 2 ⎛ψ x −α ⎞ ⎛ψ y − β ⎜ ⎟ + ⎜⎜ ⎝ dx ⎠ ⎝ d y 2 ⎞ 2 ⎟⎟ = k ⎠ Para calcular el diagrama de radiación es más conveniente realizar un cambio de escala en los ejes x,y de forma que el límite se convierta en una circunferencia de radio k. 2 2 ⎛ψ x α ⎞ ⎛ψ y β ⎞ − ⎟ +⎜ − ⎟ = k2 ⎜ ⎜ ⎟ ⎝ dx dx ⎠ ⎝ d y d y ⎠ En las gráficas se representan los diagramas de radiación de una agrupación uniforme de 3x3 antenas espaciadas 1.3λ. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 8 ψy ψx Curvas de nivel correspondientes a una agrupación plana uniforme de 3x3 antenas. r=k ψy ψx dy dx Representación gráfica del margen visible tridimensional y del diagrama de radiación para una agrupación plana uniforme de 3x3 antenas espaciadas 1.3λ. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 9 Redes de distribución de potencia Las agrupaciones de antenas requieren que se distribuya potencia a las diversas antenas, controlando su amplitud y su fase. Las técnicas de distribución de potencia se pueden clasificar en tres tipos: serie, paralelo y redes espaciales.También pueden realizarse diseños con redes de varios tipos combinadas entre sí. La redes de distribución paralelo consisten en una serie de circuitos divisores de potencia unidos mediante líneas de transmisión. Al final de la red se pueden incluir una serie de atenuadores y desfasadores para ajustar las amplitudes y fases de las corrientes en las antenas. Las redes tipo serie utilizan una línea de transmisión y un conjunto de acopladores direccionales que extraen una fracción de potencia de la línea. Al final de la línea se suele colocar una carga para evitar reflexiones de señal. Las redes de distribución espaciales utilizan la radiación de una antena para distribuir señal a un conjunto de radiadores secundarios. La señal recibida se amplifica y se ajusta en amplitud y fase. Redes de distribución de potencia serie y paralelo Red de distribución serie en una agrupación de antenas impresas. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia