φ φ φ φ φ φ φ φ
Anuncio

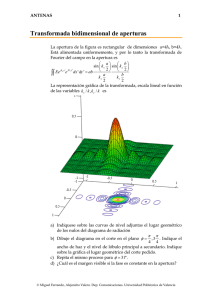
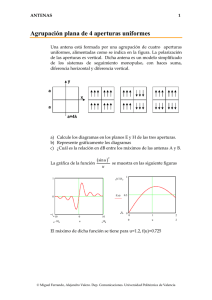
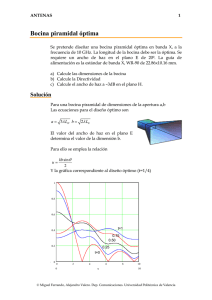
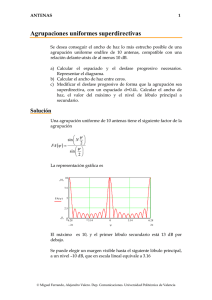
ANTENAS 1 Array con control de fase Las agrupaciones controladas por fase “phased arrays”, permiten controlar la orientación del haz. Se dispone de un sistema de 8 antenas, espaciadas 0.5λ, alimentadas a través de una red distribuidora de potencia formada por divisores simétricos (-3dB), entre cada antena y la red de distribución se intercala un sistema de control de fase con 16 niveles (4 bits). El sistema permite elegir valores discretos de fase , con saltos de 22.5 0 φ φ φ φ φ φ φ φ a) Representar gráficamente el diagrama de radiación cuando todas las antenas están conectadas en fase. b) Indicar los valores necesarios de las señales de control (formato binario), para conseguir un diagrama de radiación que apunte a un ángulo de 104.50 con respecto al eje de la agrupación. Representar el diagrama. c) Se desea que el máximo esté en la dirección 82.80, indicar las fases de cada antena, aproximando en caso necesario al valor más cercano. Indicar el error de fase con respecto al valor teórico. d) Representar gráficamente el diagrama incluyendo errores de fase. © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 2 Solución Diagrama de radiación Las amplitudes en todas las antenas son iguales, el polinomio de la agrupación es p ( z ) = 1 + z + z 2 + z 3 + .... + z 7 Eje imaginario 7 p( z ) = ∑ z n 90 120 n =0 60 0.8 Los ceros de la agrupación uniforme son las raíces octavas de la unidad. 0.6 150 0.2 180 0 n 210 330 240 300 270 El factor de la agrupación y el Diagrama (margen visible -π,π) 8 0 Eje real z 7 z −1 z8 − 1 p( z ) = ∑ z = = z −1 z −1 n =0 7 30 0.4 8 6 FA( ψ ) 4 2 0 0 3.14 2.36 1.57 0.79 −π 0 0 0.79 1.57 2.36 ψ 3.14 π 0 10 20 ⋅log( f ( θ ) ) 20 − 30 30 0 0 1 2 θ 3 π © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia ANTENAS 3 Cambio de orientación del máximo La relación entre el diagrama y el factor de array es ψ = kd cosθ + α El desfase progresivo necesario es α = −kd cos θ m = π 4 Las fases necesarias y los bits de control en cada antena son 0 0 0000 1 45 0010 2 90 0100 3 135 0110 4 180 1000 5 225 1010 6 270 1100 7 315 1110 La representación gráfica del nuevo diagrama es 0 0 10 20 ⋅log( f ( θ ) ) 20 − 30 30 0 1 2 3 θ 0 π Errores de fase Para conseguir el nuevo máximo es necesario tener un desfase progresivo de π α = −kd cosθ m 2 = − π 3.14 2.36 1.57 16 0.79 βi 0 0.79 1.57 2.36 − π 3.14 0 0 1 2 3 4 5 6 i © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia 7 7 ANTENAS 4 Los desfasadores digitales no permite obtener valores exactos, se pueden aproximar por la fase más cercana, los valores son 0 0 0000 1 0 0000 π 2 -22.5 1111 3 -22.5 1111 4 -45 1110 5 -45 1110 6 -67.5 1101 7 -67.5 1101 3.14 2.36 1.57 0.79 βi 0 0.79 1.57 2.36 − π 3.14 0 1 2 3 0 4 5 i 6 7 7 Como se puede observar aparecen errores de fase en las antenas 1,3,5,7. Diagrama de radiación El diagrama con estas fases se puede calcular numéricamente, es 0 0 10 20 ⋅log( f ( θ ) ) 20 − 30 30 0 0 1 2 θ 3 π © Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia