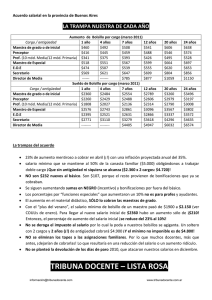
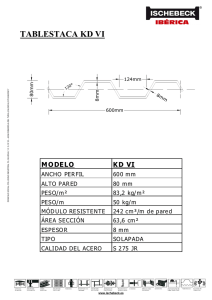
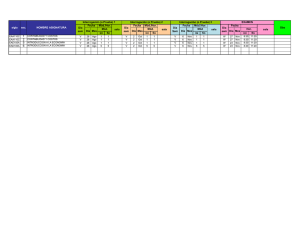
RESTOS CUADRATICOS

Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
9. RESTOS CUADRATICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
9.1 Restos cuadráticos
1.1 Concepto de restos.
Si la congruencia x ≡ a ( mód .m ) es una relación de equivalencia que permitirá clasificar a los
números enteros, y por tanto los naturales, en clases de equivalencia, conjuntos formados por
cada número entero y todos sus congruentes. En este caso se llaman clases de restos o residuales, porque cada clase se puede representar por el resto que resulta al dividir cualquier
elemento entre el módulo m.
Las clases módulo m se representan por ℤ/݉ℤ ó por ℤ݉.
1. Para ℤ / 2ℤ = {0,1} , que son los dos restos producidos al dividir entre 2. El elemento 0
representa a los números pares y el 1 a los números impares.
2. Para ℤ / 5ℤ = {0,1, 2,3, 4} , en el que, por ejemplo el elemento 3 representa a los números 3,8,13,18, 23,… , que dan resto 3 al dividir por 5.
La clase ℤ / mℤ contiene exactamente m elementos: {0,1,3, 4,5,6,…, m − 1} . A veces se usan restos mínimos, admitiendo números positivos y negativos, mediante la elección entre a y a − m
del número con menor valor absoluto.
En los sistemas algebraicos las clases de restos tienen estructura de anillo para la suma y el
producto. El grupo aditivo de ese anillo es cíclico, pues para cada elemento a del mismo existe
un h tal que a ⋅ h = 0. Ese número h ha de ser divisor del módulo m.
No todos los elementos tienen inverso. En caso afirmativo, se llaman inversibles, y su conjunto
coincide con las clases representadas por números primos con m, incluyendo el 1. Por tanto,
su número coincide con ϕ (m) = m (1 − 1 p1 ) ,…, (1 − 1 pn ) , denominado indicador de Euler o función fi. El inverso vendrá determinado por aϕ ( m) ª 1(mód .m).
Los elementos inversibles forman un grupo multiplicativo, al que representaremos por ℤ * m,
que son las clases residuales reducidas. Este carácter de grupo da lugar a que, si a es inversible en ℤ * m, existe un número natural r tal, que a r = 1. El número r mínimo que cumple la
anterior igualdad se llama, para todos los grupos ‫݊݁݀ݎ݋‬, í݊݀݅ܿ݁ ‫ܽ ݁݀ ݋݊ܽ݅ݏݏݑܽ݃ ݋‬. Es fácil
ver que si a n ≡ 1(mód .m), el exponente n deberá ser múltiplo del orden r. Otra consecuencia
es que, si a es primo con m y se cumple que a x = a y entonces, han de ser x = y.
Si m es primo, serán inversibles todos los elementos y constituirán un cuerpo.
Se llama sistema completo de restos al conjunto de m enteros tomados, cada uno de ellos, de
una de las clases de restos módulo m, donde {0,1,3, 4,5,6,…, m − 1}.
Se llama sistema reducido de restos al conjunto de m enteros tomados, cada uno de ellos, de
una de las clases de restos módulo m, que no comparten con m factores comunes. Se denotan mediante la función ϕ (m) = m (1 − 1 p1 ) ,…, (1 − 1 pn ) que da el número de enteros que son
primos con m.
Se llaman restos potenciales del número natural n, respecto a un módulo dado m, a los restos
producidos por las distintas potencias naturales de n.
El conjunto de restos potenciales sigue unas pautas muy sencillas de seguir:
1
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
1. Si m sólo contiene factores primos con n, se llegará a cierta potencia de n que será
múltiplo de m y por tanto, a partir de ella todos los restos potenciales serán nulos.
2. Si m es primo con n, los restos son periódicos en periodo gaussiano con n respecto a
m. El resto 1 se producirá en los múltiplos de ese gaussiano.
3. Si el mcd ( m, n) = d , con d > 1, los restos potenciales tendrán una parte periódica y
otra no periódica.
El sistema reducido de restos, respecto al módulo p, consta de ( p − 1) / 2 restos cuadráticos,
los cuales son congruentes con los números 12 , 22 , 32 ,..., (( p − 1) / 2) y de ( p − 1) / 2 no-restos
cuadráticos. Si a es un resto cuadrático respecto al módulo p, se tiene a ( p−1)/2 ª 1(mód . p); si a
es no resto cuadrático respecto al módulo p, entonces a ( p−1)/2 ª −1(mód . p). Esto se conoce como criterio de Euler. Según el teorema de Fermat, a p−1 ≡ 1(mód . p), luego
(a ( p−1)/2 − 1)(a ( p−1)/2 + 1) ª 0(mód. p). Esto nos lleva a que, el número de restos cuadráticos de la
forma ( p − 1) / 2 es igual al número de restos no cuadráticos.
El producto de dos restos o de dos no restos siempre es un resto cuadrático, y el producto de
Un restos cuadrático con otro no cuadrático produce un no resto.
El conjunto de restos cuadráticos forma un grupo multiplicativo en ℤ / ℤp, de índice 2.
2
1.2 Calcular los sistemas completo y reducido de restos del número 10.
El sistema completo de restos es el conjunto de m enteros, tomados cada uno de ellos, de una
de las clases de restos respecto al módulo m, esto es, {0,1, 2,3,…, m − 1} . En nuestro caso, para
el número 10 tendremos {0,1, 2,3, 4,5,6,7,8,9} . Observar que si se produce un resto 0, la divi-
sión es exacta y, por tanto, el número es de la forma 10m y genera un cociente que es divisor
de 10m.
El sistema reducido de restos es el conjunto de m enteros tomados, cada uno de ellos, de una
de las clases de restos módulo m, que no comparten con m factores comunes. La función
ϕ (m) = m ( p1 − 1 p1 ) ,…, ( pn − 1 pn ) da el número de enteros que son primos con m. En nuestro
caso, para el número 10, ϕ (10) = 10 (1 − 1 2 )(1 − 1 5) = 10 (1 2 ⋅ 4 5) = 4. Cuatro números que son
coprimos con 10, {1,3,5,7} . Es la solución del problema.
1.3 Calcular los restos potenciales de 5 respecto al módulo 13.
Si el sistema completo de restos, respecto al número 13 es {1, 2,3, 4,5,6,7,8,9,10,11,12} , los restos potenciales de 5, respecto a 13 serán {5, 12, 8, 1, 5, 12, 8, 1, 5, 12, 8, 1}, que hemos calculado de la siguiente forma:
51 ª 5
52 ª 12
53 ª 8
54 ª 1
55 ª 5
56 ª 12
57 ª 8
58 ª 1
59 ª 5
510 ª 12
511 ª 8
512 ª 1
Si observamos los cálculos anteriores, podemos establecer un método sencillo para obtener
estos restos.
Supongamos que r1 , r2 , r3 ,… , rh son los restos de n respecto al módulo m, esto es,
2
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
n ª r1 (mód .m)
n 2 ª r2 (mód .m)
n3 ª r3 (mód .m)
⋯⋯
h
n ª rh (mód .m)
Entonces, para encontrar el resto rh+1 de la potencia nh+1 , bastará multiplicar las congruencias
primera y última anteriores, es decir, n ⋅ nh = n h +1 ª r1 ⋅ rh ( mód .m), por lo que bastará con calcular r1 ⋅ rh ( mód .m), siendo r1 ⋅ rh un número más pequeño que n h +1 .
En nuestro caso particular
51 ª 5(mód .13)
52 = 25 ª12(mód .13)
53 = 52 ⋅ 5 ª 8(mód .13)
54 = 52 ⋅ 52 ª1(mód .13)
⋯⋯
1.4 Calcular los restos cuadráticos respecto al módulo 17.
El sistema completo de restos, respecto al módulo 17 es {1, 2,3, 4,5, 6, 7,8,9,10,11,12,13,14,15,16} .
El sistema cuadrático de restos, respecto a 17 es {1,4,9,16,8,2,15,13,13,15,2,8,16,9,4,1}, que
hemos calculado de la siguiente forma:
12 ª 1
22 ª 4
32 ª 9
4 2 ª 16
52 ª 8
62 ª 2
7 2 ª 15
82 ª 13
9 2 ª 13
10 2 ª 15
112 ª 2
12 2 ª 8
132 ª 16
14 2 ª 9
152 ª 4
16 2 ª 1
Observar que los restos cuadráticos, respecto a un módulo, forman parejas donde la suma de
las bases es igual al módulo. Esto forma un conjunto simétrico que nos permite obtener la totalidad de restos cuadráticos utilizando sólo la mitad de los números base. Veamos cómo:
12 y 162 ª 1(mód .17)
52 y 122 ª 8(mód .17)
22 y 152 ª 4(mód .17)
62 y 112 ª 2(mód .17)
32 y 142 ª 9( mód .17)
72 y 102 ª 15(mód .17)
42 y 132 ª 16(mód .17)
82 y 92 ª 13(mód .17)
1.5 Resolver la ecuación x 2 + 8 ≡ 0(mód .11).
La ecuación x 2 + 8 ≡ 0(mód .11) se puede escribir como x 2 ≡ 3(mód .11). Esta ecuación
tendrá solución sí, y sólo si, 3 es un resto cuadrático respecto al módulo 11.
Los restos cuadráticos respecto al módulo 11 son {1,4,9,5,3,3,5,9,4,1} donde aparece el número 3 luego, la ecuación tiene solución. Dado que el número 3 se encuentra en el epicentro del
3
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
11 − 1
11 + 1
=5 y
= 6, estas
2
2
serán las soluciones de la ecuación. Efectivamente, 52 − 3 = 22 = 2 ⋅11 y 6 2 − 3 = 33 = 3 ⋅11.
conjunto de restos, y dado que las bases de este epicentro serán
Podemos decir que, del sistema completo de restos {1, 2,3, 4,5,6,7,8,9,10} , el 5 y el 6 satisfacen a la ecuación.
Para la determinación de si un número es o no resto cuadrático respecto a un módulo m, podemos utilizar el criterio de Euler, a ( p−1)/2 ª ±1(mód .m), con m primo y donde a representa el
número a investigar. Para nuestro caso, 3(11−1)/2 = 35 ª 1(mód .11), donde el resto de la unidad positiva denota que 3 es resto cuadrático respecto al módulo 11.
1.6 Si a es restos cuadrático respecto al módulo p, siendo mcd ( a , p ) = 1, demostrar
que x 2 ≡ a(mód . p) admite dos soluciones.
Si a es resto cuadrático, la congruencia x 2 ≡ a(mód . p) admite la solución x ≡ x1 (mód . p)
entonces, como (− x1 ) 2 = x 2 , la misma congruencia admitirá una segunda solución, esto es,
x ≡ − x1 (mód . p), que es distinta a la anterior. Luego, x 2 ≡ a(mód . p) admitirá como soluciones x ª x1 , x2 (mód . p ) si, y sólo si, a es resto cuadrático respecto al módulo p.
1.7 Resolver la ecuación x 2 ≡ 3(mód .13). .
Si aplicamos el criterio de Euler, 3(13−1)/ 2 = 36 ª 1(mód .13) que denota que el 3 es resto cuadrático respecto al módulo 13.
El sistema completo de restos del número 13 es {1, 2,3, 4,5,6,7,8,9,10,11,12} , de los que el
4 y el 9 satisfacen a la ecuación x 2 ª 3(mód .13) por tanto, x1 = 4 + 13t y x2 = 9 + 13t son
sus soluciones.
El sistema cuadrático de restos respecto al módulo 13 es:
12 y 122 ª 1(mód .13)
42 y 92 ª 3(mód .13)
22 y 112 ª 4(mód .13)
52 y 82 ª12(mód .13)
32 y 102 ª 9( mód .13)
62 y 7 2 ª 10(mód .13)
1.8 Resolver la ecuación x 2 ≡ 19(mód .29). .
Mediante el criterio de Euler, 19(29−1)/ 2 = 1914 ª -1(mód .29), que indica que 19 no es resto
cuadrático respecto al módulo 29. Efectivamente, el sistema de restos cuadráticos respecto a
29, es
{1, 4,9,16,25,7, 20,6, 23,13,5, 28, 24, 22,22, 24, 28,5,13, 23,6, 20,7,25,16,9, 4,1}
en donde no aparece el número 19, por tanto, la ecuación no tiene solución.
1 2 3 4 5 6 7 8 9 10 11 12 13 14
28 27 26 25 24 23 22 21 20 19 18 17 16 15
Raíces
1 4 9 16 25 7 20 6 23 13 5 28 24 22
Observar la simetría de las bases del exponente formando parejas cuya suma es 29.
4
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
9.2 Símbolos de Legendre y Jacobi
2.1 Símbolo de Legendre y sus propiedades.
Sea p un primo impar. Diremos que un número natural a primo con p es un resto cuadrático módulo p si x 2 ª a (mód . p), para cierto entero x. En caso contrario, siempre suponiendo que p es primo, diremos que a es un resto no cuadrático. Se conoce como símbolo de Legendre a la expresión
 1 si a es resto cuadratico módulo p

a
 p  = ( a p ) = −1 si a es resto no cuadrático módulo p
 
 0 si p 6 a

Si a es un resto cuadrático respecto al módulo p, se tiene a
cuadrático respecto al módulo p, se tiene a
(
Fermat, a p −1 ª 1(mód . p) donde a
p −1
2
p −1
2
)(
ª 1(mód . p). Si a es un no
ª -1(mód . p). En efecto, según el teorema de
)
p −1
2
-1 a
p −1
2
+ 1 ª 0(mód . p). De aquí podemos deducir
a
que a ( p −1)/ 2 ª   ( mód . p ) que nos permite la solución a la ecuación x 2 ª a (mód . p) aplicando
 p
propiedades del símbolo de Legendre.
El símbolo de Legendre satisface algunas propiedades interesantes como:
a
b
i.
Si a ª b( mód . p ), entonces   =   . Esta propiedad se debe a que los números de
 p  p
una misma clase son simultáneamente restos o no restos cuadráticos.
ii.
Si a ª 1( mód . p ), tenemos   = 1. En efecto, 1 = 12 y, por tanto, 1 es un resto
 p
cuadrático.
iii.
Si a ª -1(mód . p), entonces   = ( −1) 2 . Esta propiedad se deduce de la anterior
 p
para a = −1 y denota un resto no cuadrático.
iv.
Si a ª 2(mód . p), entonces   = ( −1)
 p
v.
Si a ª -3( mód . p), entonces   = 
.
 p   −1 si p ª 5(mód .6)
vi.
Si a ª 5(mód . p ), entonces   = 
.
 p  −1 si p ª 3, 7(mód .10)
vii.
Sea  p  =  p  p  p  . Se deduce, en particular, que  p  =  p  p  p  =  p  ,

    

      
1
 −1 
2
 −3 
5
 abb 
p −1
p 2 −1
8
.
 1 si p ª 1(mód .6)
 1 si p ª 1,9(mód .10)
 ab 2   a  b  b   a 
 a  b  b 
2
b
ya que  p  = 1. Esto significa que en el numerador del símbolo de Legendre se puede
 
eliminar cualquier factor cuadrático.
viii.
q
 p −1   q −1 
 ⋅

2  2 
Si p y q son números primos impares,   = ( −1)
 p
nocida como Ley de Reciprocidad Cuadrática.
 p
 q  . Esta propiedad es co 
5
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
Nota: La Ley de Reciprocidad Cuadrática tiene un papel muy importante en la teoría de los números, ya
que en base a ésta, se han obtenido otros resultados interesantes en diversos campos de las matemáticas.
Descubierta por ‫ ( ݎ݈݁ݑܧ‬1707 − 1783) en 1742, gracias a los trabajos realizados por ‫( ݐܽ݉ݎ݁ܨ‬1601 −
1665, revisada en 1772, fue publicada en su Opuscula Analitica de 1873, después de su muerte.
‫( ݁ݎ݀݊݁݃݁ܮ‬1752 − 1833) fue otro de los pioneros en el estudio de esta ley, de hecho fue el primero en
dar una demostración. Basándose en los trabajos de Euler, en 1798 publica en su obra Essai sur la Théorie
des Nombres un lema que hoy se conoce como símbolo de Legendre. El primero que ofrece una demostración completa de la Ley de Reciprocidad Cuadrática fue ‫( ݏݏݑܽܩ‬1777 − 1855), a la que llama Theorema Aureum (Teorema áureo), recogida en su obra Disquisitiones Arithmeticae y publicada en 1796.
2.2 Símbolo de Jacobi y sus propiedades.
n (
 ó n / m ) para números impares m con
m
Consideremos el símbolo 
m > 1, no necesaria-
mente primos, donde m = p1 ⋅ p2 ⋅… ⋅ pn , con mcd (n, m) ≠ 1.
El Símbolo de Jacobi se define como
 n   a  b   l 
  =   …  
 m   p1  p2   pn 
Sus propiedades son similares a las propiedades al Símbolo de Legendre.
El uso del Símbolo de Jacobi proporciona la generalización del Símbolo de Legendre y la del
 m  n 
teorema de los recíprocos cuadráticos    = ( −1)
 n  m 
mos enteros, con n ≥ 3. Esta igual es equivalente a
( m −1)( n −1)/ 4
, para
m, n relativamente pri-
( m −1)( n −1)/ 4  n 
m
 n  = ( −1)
m
 
 
que también podemos escribir como:
 m
 +   para m ó n ª1(mód .4)
n  n
.
m= 
   m
−
para m, n ª 3(mód .4)
  n 
Estos es lo que hemos definido anteriormente como Ley de Reciprocidad Cuadrática.
2.3 Demostrar que si p es primo y a y b son dos enteros con a ª b( mód . p ), ena
b
tonces   =   .
p
p




a
El valor de   depende sólo de si a es restos cuadrático, esto es, si x 2 ª a (mód . p) tiene
 p
solución. Como esto sólo depende de la clase de equivalencia de a respecto a p, se verifica
a
b
que   =   si, y sólo si a ª b( mód . p ).
 p  p
6
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
a
Si p es primo y mcd ( a , p ) = 1, obtenemos   ª a ( p −1)/ 2 (mód . p), que es el criterio de Euler.
 p
Por el pequeño teorema de Fermat sabemos que a p −1 ≡ 1(mód . p), esto nos permite deducir
que ( a p −1 ) ≡ a p −1 ≡ ±1( mód . p ), y para que a p −1 ≡ 1(mód . p) será necesario que   = 1.
 p
a
2
Por ejemplo, si a = 7 y p es de la forma p ≡ 1(mód .4), tenemos
 7   p   1 si p ≡ 1, 2, 4(mód .7)
 = =
 p   7   −1 si p ≡ 3,5,6(mód .7)
Si p es de la forma p ≡ 3(mód .4), tenemos
7
 p   1 si p ≡ 3,5,6( mód .7)
  = −  = 
 7   −1 si p ≡ 1, 2, 4(mód .7)
 p
o, también
 7   1 si p ≡ 1,3,9,19, 25, 27(mód .28)
 =
 p  −1 si p ≡ 5,11,13,15,17, 23(mód .28)
2.4 Demostrar que si p es primo y a y b son dos enteros no divisibles con q, enab
a b
tonces   =     .
 p
 p  p 
a
Sabemos que a ( p −1) / 2 ª   (mód . p), entonces ( ab )
p

( p −1) / 2

a
 ab 
ª   (mód . p) donde
 p
 ab 
b
mcd (ab, p) = 1,
 a  b 
como a ( p −1)/ 2 ª   (mód . p ) y b( p −1)/ 2 ª   (mód . p), se cumple que   ª    (mód . p ), y
 p
 p
 p   p  p 
 ab 
 a  b 
 ab 
como p no es par,   =     , luego   = a ( p −1) / 2 b( p −1) / 2 = ( ab )
 p   p  p 
 p
( p −1) / 2
 a  b 
ª    (mód . p).
 p  p 
2
2
2.5 Demostrar que si p es impar, entonces  p  = ( −1) ( p − 1) / 2.


a
k
Sea   = (−1) donde k es el número de restos que son mayores que p / 2, como
 p
8
(−1) ≡ k (mód .2), entonces
2
 2 
  = (−1)k = (−1)( p −1)/8

 p 
7
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
El profesor Vinogradov llega a esta conclusión utilizando el Símbolo de Jacobi. Este matemático
dice que si P es impar mayor que la unidad, esto es, m = p1 ⋅ p2 ⋅ ...⋅ pn que es la descomposición
 
m
a
factorial de P, y si el mcd (a, P ) = 1, entonces el Símbolo de Jacobi   se define por la igual 
dad:
2
 a   a   a   a   2 
  =  ⋅  ⋅ ...⋅   =   = (−1)( p −1)/8
 m   p1   p2   pr   p 
A partir de lo expuestos podemos obtener otras igualdades como
 a   ab 2 
 p  =  p  ,
  

 1 
 
  = 1 ó  1  = (−1)( p−1)/ 2
 p 
 p 
 1 
  = (−1)( p −1) / 2
 p 
y también
 a + p   a + p 
 2a   2a + 2 p   4 2   2 
  = 
=
=

 p  
p   p   p 
 



 

que nos lleva a que
p
1 
ax  p 2 −1
 2 

 +
 p 
8 ,
  a  = (−1)∑

x=1
 p 
 p 
de la que nos permite deducir dos propiedades muy importantes del Símbolo de Legendre. La
primera es que para a = 1:
2
 2 
  = (−1)( p −1)/8
 p 
la segunda es que si p es de la forma p = 8m + s, donde s es uno de los números 1, 3, 5, 7, y
además
 p 2 −1
s 2 −1

 = 8m2 + 2ms +
 8 
8
entonces este número será par si s = 1 ó s = 7, e impar si s = 3 ó s = 5. Por tanto, el
número 2 será resto cuadrático respecto al módulo p si p es de la forma p = 8m + 1 ó
p = 8m + 7 y será no resto cuadrático respecto al módulo p si p es de la forma p = 8m + 3
ó p = 8m + 5.
8
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
2.6 Demostrar que si P y Q son números impares positivos, primos entre sí, enQ
( P −1)( Q −1)/ 4  P 
tonces   = ( −1)
 .
P
Q
 P −1   Q −1 
Como 
 ⋅
 es impar solamente cuando ambos números, P y Q, son de la forma
 2   2 
4m + 3, y es par si al menos uno de estos números es de la forma 4m + 1, la propiedad señalada se puede formular así:
Q
P
Si ambos números, P y Q, son de la forma 4m + 3, entonces   = −   .
P
Q
Q
P
Si al menos uno de los números, P y Q, es de la forma 4m + 1, entonces   =   .
 P Q
Supongamos que Q = q1 ⋅ q2 ⋅… ⋅ qn es la descomposición de Q en factores primos, se tiene
s
t
Q
 Qβ 
Q  Q   Q 

  =   ⋅   ⋅… ⋅   = ∐ ⋅∐ 
 P   p1   p2 
 pn  α =1 β =1  Pα 
y como
s
t
Q 
=1
=1

 r Pα −1   s Qβ −1 





 α =1 2   β =1 2 
β
∑
⋅∐ 
 = ( −1)
∐
P
α
β

α
∑
s
P 

=1 
β 
t
⋅∐  α
∐
Q
α
β
=1
resulta:


P −1
 ∑ α  ∑
Q


 P  = ( −1) α =1 2  β =1
 
r
s
Qβ −1 

2 

P
.
Q
Si ahora hacemos que
P − 1 r Pα − 1
Q − 1 s Qβ − 1
=∑
+ 2N y
=∑
+ 2 N1 ,
2
2
2
2
β =1
α =1
entonces:
( P −1)( Q −1)/ 4  P 
Q
  = ( −1)
 Q .
P
 
2.7 Resolver la ecuación x 2 ª 28(mód .37).
 28 
 22 ⋅ 7 
 2⋅2⋅7 
 2   37 
Sea   = 
=
 . Para  37  =  2  ( −1)
   
 37   37   37 
(372 −1)/8
1
=   = 1, ya que
2
37 ª 1(mód .2).
 28 
Por tanto, como   = 1, 28 es resto cuadrático respecto al módulo 37, y la ecuación plantea 37 
da tiene solución. Efectivamente, del sistema completo de restos respecto al módulo 37, la
9
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
pareja central compuesta por el 18 y 19, satisfacen a la ecuación x 2 ª 28(mód .37), por tanto
son sus soluciones.
Dado que 28 = 22 ⋅ 7 y sabiendo por vii que en el numerador del Símbolo de Legendre se
pueden eliminar cualquier factor cuadrático, resulta para:
2
 28   2 ⋅ 7   7 
= 
 =
 37   37   37 
Utilizando la Ley de Reciprocidad Cuadrática
((37 −1)(7 −1))/ 2
 7   37 
 37   2 
= = 
 37  =  7  ( −1)
   
 7  7
ya que 37 ª 2(mód .7).
2
Como   = ( −1)
7
37.
(72 −1)/8
 28 
= 1, resulta para   = 1, por tanto 28 es restos cuadrático respecto a
 37 
2.8 Resolver la ecuación x 2 ª 174(mód .239).
 174 
 2   3  29 
Como 174 = 2 ⋅ 3 ⋅ 29, 
=


.
 239   239   239  239 
Por la Ley de Reciprocidad Cuadrática, se tiene que
 2   239 
(2392 −1)/8
 3   239 
(239 −1)/ 2
 29 
(239/ 2)(28/ 2)
Para 
=
 ( −1)
 239   2 
Para 
=
 ( −1)
 239   3 
 239 
Para 
=
 ( −1)
 239   29 
 7   29 
Para   =   ( −1)
 29   7 
(28/ 2)(8/ 2)
= 1, ya que
239 ª1(mód .2).
 239 
 2 1
= −
 = −  3  =  3  = 1, ya que
 3 
   
 239   7 
= −
 =   = 7, ya que
 29   29 
 29   7 
=   =   = 1, ya que
 7   29 
3 ª1(mód .2).
239 ª 7(mód .29).
29 ª1(mód .7).
Como
 174   2   3   29 
 239  =  239   239   239  . = (+1)(+1)(+1) = 1 174

 



es restos cuadrático respecto a 239 por tanto, la ecuación x 2 ª 174(mód .239) tiene como solución x ª 37, 202(mód .239).
10
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
2.9 Resolver la ecuación x 2 ª 864(mód .857).
 864 
 25  33   2  3 
Como 864 = 25 ⋅ 33 , 

=
=

.
 857   857  857   857  857 
Por la Ley de Reciprocidad Cuadrática, se tiene que
 2   857 
(857 2 −1)/8
 3   857 
(857 −1)/ 2
Para 
=
 ( −1)
 857   2 
Para 
=
 ( −1)
 857   3 
= 1, ya que 557 ª 1(mód .2).
2
=   = −1, ya que 2 + 1 ª 0(mód .3)
3
Como
5
3
 864   2  3   2  3 
=


=



 = (+1)(−1) = −1, 864
 857   857  857   857  857 
no es resto cuadrático respecto al módulo 857, por tanto x 2 T 864(mód.857) no tiene solución.
9.3 Símbolo de Kronecker y Lema de Gauss
3.1 Símbolo de Kronecker y sus propiedades.
n (
 ó n / m ) , es una extensión del
m
El Símbolo de Kronecker, que podemos denotar como 
Símbolo de Jacobi, descubierto por el matemático alemán Leopold Kronecker (1823-1891) y
que comparte las mismas reglas que éste.
Algunas de sus propiedades son:
 n  −1 si n < 0
Para m =−1,   = 
 −1   1 si n > 0
 0 para n par
 n  
Para m = 2,   ª  1 para n impar, n ª ±1(mód.8)
 2  
 −1 para n impar, n ª ±3(mód.8)
 0 para 4 | n
 n  
o también,   ª  1 para n ª 1(mód.8)
 2  
 −1 para n ª 5(mód.8)
 85 
3.2 Utilizando el símbolo de Kronecker, resolver   . .
 2
 85 
Como   = −1, entonces 85 ª 5(mód.8).
 2
11
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
 131 
3.3 Utilizando el símbolo de Kronecker, resolver 
. .
 248 
 131 
Como 248 = 8 ⋅ 31, 
 = −1 ya que 131 ª 3(mód.8).
 8 
3.4 Lema de Gauss: definición.
 p − 1 
Sea p un primo impar, sea ܽ un entero no divisible por ‫ ݌‬y sea u = 
. Si al dividir los
 2 
números {a ,2a ,3a ,… , a [(p− 1) / 2]} por ‫ ݌‬hay exactamente ‫ ݏ‬elementos cuyo resto es mayor
a
que ‫ݑ‬, entonces   = (−1)s . Esto se conoce como Lema de Gauss en honor a Carl Friedrich
 p
Gauss (1777-1855) que la descubrió.
a
Por el criterio de Euler,   ª au (mód.p), como u ! no es divisible por ‫݌‬, obtenemos:
 p
a u ª (− 1) s (mód . p)
luego
 
 a  ª (−1)s (mód.p)
 p 
 5
3.5 Utilizando el lema de Gauss, resolver   .
 17 
17 − 1
= 8. Si multiplicamos por 5 los números entre 1 y 8, obte2
nemos {5,10,15,20,25,30,35 y 40}. Estos números, respecto al módulo 17, generan el siste-
Tenemos p = 17, a = 5 y s =
ma de restos {5,10,15,3,8,13,1,6} de los que {10,15 y 13} son mayores que u = 8, por tanto
 5 

= (−1)3 =−1
 17 
que es lo mismo que 58 ª (−1)3 (mód.17) ⇒ 58 +1ª (mód.17).
5
3.6 Utilizando el lema de Gauss, resolver   .
 31 
31 − 1
p
= 15 y = 15,5. Sea E = {5, 2 ⋅ 5,3 ⋅ 5,...,15 ⋅ 5} , los residuos módulo 31
2
2
de los elementos de E son
Tenemos que s =
E = {5,10,15, 20, 25,30,,9,14,19, 24, 29,3,8,13}
luego el conjunto de los elementos de E mayores que 15,5 vienen determinados por
12
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
A = {19, 20,24, 25,29,30}
entonces tenemos que A = 6, de donde
5
= (−1)6 = 1
31
Esto queda demostrado por la función generatriz o criterio de Euler, ya que, si tenemos en
cuenta que 5(31−1)/ 2 ≡ 1(mód .31), la ecuación x 2 ≡ 5( mód .31) tiene como solución las raíces
primitivas x1 = 6 + 31t y x2 = 25 + 31t.
3
3.7 Utilizando el lema de Gauss, resolver   .
 13 
Del conjunto {3,6,9,12,15,18} son restos respecto a 13 {3,6,9,12, 2,5}. De estos hay dos elementos que son mayores a 13 2, luego
3
2
  = (−1) = 1
 13 
3.8 Lema de Eisenstein: definición.
u
Sea ‫ ݌‬un número primo impar y sea ܽ un entero no divisible por ‫݌‬. Sea s = ∑[ ja p].
j=1
a
Si ܽ es impar, entonces   = (−1)s .
 p
2
2
Si ܽ = 2, entonces   = (−1)( p −1)/8 .
p
 
Si hacemos que
u
u
∑ ja =∑( ja
j=1
j=1
u
u
p)p + ∑ rj = sp + ∑ rj + ∑ rj y si
j=1
rj ≤u
rj >u
∑ j =∑ r + ∑ (p − r )
j
j=1
rj ≤u
j
rj >u
restando ambas ecuaciones obtenemos
u
(a − 1)∑ j =sp − pl + 2∑ rj
j=1
rj >u
Si ܽ es impar, entonces (a - 1) ª 0(mód.2), p ª 1(mód.2) y l ª s(mód.2). El resultado se sigue por el
Lema de Gauss.
Supongamos que ܽ = 2. Si 1 ≤ j ≤ u, tenemos (2 j p) = 0 puesto que p > 2 j. Así, s = 0.
Como
13
Rafael Parra Machío
u
∑j=
j=1
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
u(u + 1) p2 − 1
=
2
8
podemos establecer que
p2 − 1
ª l(mód.2), resultado que se sigue por el Lema de Gauss.
8
El Lema de Eisenstein fue descubierto por el matemático alemán Ferdinand Gotthold Eisenstein(1823-1852).
3.9 Determinar todos los números primos impares p tales que 3 es restos cuadrático . (mód . p).
Por la Ley de Reciprocidad Cuadrática, tenemos que
 3  p
( p −1)/ 2
  =   (−1)
p
3


 
de donde
 1 
   si p ≡ 1( mód .3)
 3   3 
 =
 p   1  si p ≡ 2(mód .3)
 3 
y
 1 si p ≡ 1(mód .4)
(−1)( p −1)/ 2 = 
-1 si p ≡ 3(mód .4)
por tanto
3
  =1
 p
si, y solamente si
p ≡ 1(mód .3), p ≡ 1(mód .4) ó p ≡ 2(mód .3), p ≡ 3(mód .4)
es decir:
p ≡ 1( mód .12) ó p ≡ 11(mód .12)
14
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
9.4 Algunas Aplicaciones: Pascua de Resurrección
4.1 Calendario Juliano
Calendario solar hecho en tiempos de Julio César por el astrónomo griego de Alejandría, Losígenes, el año 45 a.C. con la intención de aplicarlo a todo el Imperio de Roma. Constaba
de doce meses y consideraba como bisiestos todos los años cuyo número de días fuera divisible por 4, aunque terminasen el siglo. Cada mes estaba dedicado devocionalmente a un dios:
Enero estaba dedicado a Jano y a la diosa Juno; Febrero, a Neptuno; Marzo, a Minerva; Abril, a
Venus; Mayo, a Apolo; Junio, a Mercurio, Julio, a Júpiter; Agosto, a Ceres; Septiembre, a Vulcano; Octubre, a Marte; Noviembre, a Diana, y Diciembre, a Vesta.
Al establecerse el cómputo anual a partir del año del Trópico de Cáncer, cuya duración
es de 365 días y 6 horas, exactamente, se producía un error de 11 minutos y 12 segundos de
exceso por cada año, lo que provocaba la aparición de un día de más en el equinoccio cada 129
años. El calendario juliano estuvo vigente en Inglaterra hasta 1752, aunque en el resto del
mundo occidental desde el año 1582 ya se había adoptado el calendario gregoriano, modificado por mandato del papa Gregorio XIII. En la actualidad todavía lo conservan los cismáticos
griegos, y en las naciones musulmanas lo utilizan para los cálculos astronómicos y los usos en
la agricultura.
4.2 Calendario Gregoriano
Calendario establecido por el papa Gregorio XIII en el año 1582 a partir de una serie de
modificaciones hechas sobre el calendario juliano: corrió diez días en el mes de octubre y no
contabilizó como bisiestos los años que terminan siglo, excepto cuando caen en decena de siglo. En la actualidad es el adoptado por el mundo occidental, salvo los griegos ortodoxos.
Pese a todas las correcciones, ajustes y mejoras, el calendario juliano, que establecía
un año equivalente a 365'25 días, no llegaba a ajustarse de manera precisa a la duración de
365'242199 días del año trópico. La diferencia de 11 minutos y 14 segundos por año fue acumulándose, lo que motivó, por ejemplo, serias preocupaciones entre los participantes en el
Concilio de Nicea (325), donde se comprobó que el equinoccio de primavera había coincidido
con la fecha del 21 de marzo en vez de con el 25 de marzo previsto. El desajuste de 10 días que
se alcanzó en 1545 era ya lo suficientemente importante como para que el Concilio de Trento
autorizase e instase a su corrección al Papa Pablo III. Tras algunos años en que se sucedieron
diversos estudios y propuestas de reforma, el Papa Gregorio XIII confió en 1572 la cuestión al
astrónomo jesuita Cristóbal Clavius (1537-1612) y en 1582 se llegó al acuerdo de abolir el calendario juliano (que siguen utilizando sólo los ortodoxos griegos y algunas naciones musulmanas con fines astronómicos y agrícolas), corregir el desajuste de diez días, comenzar un nuevo
cómputo del calendario y establecer una nueva duración del año equivalente a 365'2422 días,
con lo que la diferencia con respecto al año trópico quedaría reducida a un exceso de 3 días
cada 10.000 años, mucho más de acuerdo con el ciclo natural de lo que nunca estuvo el calendario juliano. Además, si anteriormente el calendario juliano contaba como bisiestos todos los
años cuyo número fuera divisible por 4, aunque terminasen siglo, el calendario gregoriano estipuló no computar como bisiestos los años que terminasen siglo excepto cuando cayesen en
decena de siglo; es decir, que estableció que el último año de cada siglo dejara de ser bisiesto
en el nuevo sistema, salvo cuando se tratara de un múltiplo de 400 (1600, 2000, 2400, etc.). En
aplicación de las nuevas normas sobre el calendario, el jueves 4 de octubre de 1582 fue seguido por el viernes 15 de octubre de 1582.
La adopción del nuevo calendario gregoriano planteaba problemas de adaptación que
encontró serias resistencias en numerosos países. Aunque algunos lo aceptaron en los primeros años de su vigencia, algunas naciones no católicas no lo hicieron hasta el siglo XVIII e inclu-
15
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
so siglos posteriores: Gran Bretaña y sus colonias lo adoptaron en 1752, la URSS en 1918, y
Grecia en 1923, si bien la celebración de sus fiestas religiosas sigue rigiéndose por el calendario
juliano. En la actualidad, el calendario gregoriano ha logrado una implantación prácticamente
universal, aunque algunos pueblos siguen usando, aunque limitados mayormente a las celebraciones festivas y religiosas, calendarios propios. Tal sucede con los países de religión musulmana, judía e hindú. A pesar de que su cómputo empieza en la fecha que tradicionalmente
se consideró como la del nacimiento de Cristo, la documentación histórica indica que en realidad el Cristo histórico debió nacer 4 años antes del inicio del calendario cristiano.
4.3 Los Cómputos
Procedentes del latín computare (calcular), han llegado hasta nuestros días las palabras cómputo (cálculo), computación (método de cálculo), contar y demás voces derivadas de
la misma etimología. El idioma inglés la ha tomado para designar el computer, que ha pasado a
nuestro idioma como computador (o computadora), palabra de uso corriente junto con ordenador, de origen francés. Los elementos del cómputo anual son: la letra dominical, el número
áureo, la epacta, el ciclo solar y la indicción romana.
I.
II.
III.
IV.
V.
La letra dominical, de la A a la G, indica qué día de la semana es el primer domingo del
año: A (1 de enero), B (2 de enero), C (3 de enero), D (4 de enero), E (5 de enero), F (6
de enero) y G (y de enero). Si el año es bisiesto, se indican dos letras: a la letra correspondiente se le añade la precedente. Así por ejemplo, para el año 1972, BA, para 1956,
AG.
El número áureo indica el lugar que ocupa un año en un periodo de 19 años, intervalo
tras el cual las lunaciones recaen casi en los mismos días. Los periodos se inician en el
año 1 de la era cristiana al que se asignó el número 2. La finalidad del número áureo es
establecer la correspondencia del año lunar. Por ejemplo los últimos periodos han sido/serán 1957-1975; 1976-1994; 1995-2014.
La epacta indica la edad de la lunación justo antes del 1 de enero, para un periodo de
29 años. Una lunación exacta (tiempo entre dos lunas nuevas) dura 29 días, 12 horas,
44 minutos y 2,8 segundos. Llamamos luna nueva al momento en que la Luna no es visible desde la Tierra. La epacta es 0 si la luna nueva cae en 31 de diciembre, 5 si la luna
nueva tiene 5 días (cayó el 26 de diciembre).
El ciclo solar es un periodo de 28 años julianos que lleva los mismos días de la semana
en las mismas fechas del mes. Los últimos periodos han sido 1952-1979; 1980-2007.
La indicción romana indica el lugar que ocupa un año en un periodo de 15 años que se
renuevan perpetuamente. Se obtiene sumando 3 al número del año y dividiendo el resultado por 15. El residuo expresa la indicción de dicho año. Si no hay residuo, la indicción es 15. Las bulas papales se fecha según la indicción. Los últimos periodos de indicción han sido 1978-1992; 1993-2007.
4.4 La fecha de Pascua de Resurrección
La epacta se utiliza para calcular la fecha de Pascua. En el concilio de Nicea del año
325, se estableció que la fiesta de Pascua de Resurrección debe celebrarse el domingo siguiente al plenilunio posterior al 21 de marzo, día del equinoccio de primavera. La Pascua debe situarse entre el 22 de marzo y el 25 de abril. La fecha de Pascua condiciona las demás celebraciones cristianas:
16
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
Miércoles de Ceniza
Primer domingo de Cuaresma
Jueves Santo
Viernes Santo
Ascensión
Pentecostés
Trinidad
Corpus Christi
Sagrado Corazón
: 46 días antes de Pascuas
: 42 días
: 3 días
: 2 días
: 9 días después de Pascua
: 49 días
: 56 días
: 63 días
: 68 días
4.5 Cálculo de la fecha de Pascua de Resurrección.
Antes de proseguir es preciso dejar claro que en términos astronómicos, el equinoccio
puede tener lugar el 20 o el 19 de marzo, si bien en el calendario gregoriano se establecen
unas fechas astronómicas que, aún difiriendo ligeramente de las fechas astronómicas reales,
son las que se emplean para el cálculo. Así las cosas, queda claro que la Pascua de Resurrección no puede ser antes del 22 de marzo ( en caso de que el plenilunio fuese sábado ), y tampoco puede ser más tarde del 25 de abril, ( suponiendo que el 21 de marzo fuese el día siguiente al plenilunio, habría que esperar una lunación completa (29 días ) para llegar al siguiente plenilunio, que sería el 18 de abril, el cual, si cayese en domingo, desplazaría la Pascua
una semana para evitar la coincidencia con la pascua judía, quedando: 18+7 el 25 de abril).
Si bien durante el Renacimiento se extrajeron tablas de cálculo para la Pascua en función del número áureo y otras más complejas, hoy en día la fórmula más sencilla de calcular
esta fecha es mediante la fórmula desarrollada por Gauss. Esta fórmula requiere la definición
de cinco variables, a, b, c, d y e. Además de dos constantes M y N , que para los años comprendidos entre 1900 y 2300 tomarán los siguientes valores:
Años
1900-2099
2100-2199
2200-2299
M
24
24
25
N
5
6
0
Llamando A al año del que queremos calcular la Pascua, los valores de las variables establecidas son:
A ≡ a(mód .19), A ≡ b(mód .4), A ≡ c(mód .7)
19a + M ≡ d (mód .30), 2b + 4c + 6d + N ≡ e(mód .7)
Interpretación:
Si d + e < 10, entonces la Pascua caerá el día (d + e + 22) de marzo.
Si d + e > 9, entonces la Pascua caerá el día (d + e − 9) de abril.
Si la fecha obtenida es el 26 de abril, la Pascua caerá el 19 de abril.
Si la fecha obtenida es el 25 de abril, con d = 28, e = 6 y a > 10, entonces la Pascua caerá en el 18 de abril.
Vamos a calcular la fecha de Pascua correspondiente al año 2011. Aplicando las fórmulas anteriores, obtenemos para a = 16, b = 3, c = 2. Ahora:
19 ⋅16 + 24 ≡ 28(mód .30) y 2 ⋅ 3 + 4 ⋅ 2 + 6 ⋅ 28 + 5 ≡ 5(mód .7)
Como 28+5=33>9, entonces 33-9 corresponde al 24 de abril de 2011 que se celebrará la Pascua
de Resurrección.
Por este mismo procedimiento podemos conocer que la Pascua de Resurrección caerá
el 8 de abril en 2012 y en 31 de marzo en 2013.
17
Rafael Parra Machío
RESTOS CUADRÁTICOS Y LEY DE RECIPROCIDAD CUADRÁTICA
BIBLIOGRAFIA:
APOSTOL, Tom M., Cálculus Tomo I, ISBN: 84-291-5002-1
BOLKER, Ethan D., Elementary Number Theory, ISBN: 0-486-45807-5
CRANTZ, Paul, Aritmética y Álgebra, Edición 1926
JOUETTE, André, El Secreto de los Números, ISBN: 84-95601-00-1 (Todo el tema relacionado
con la fecha de Pascua)
KOSHY, Thomas, Elementary Number Theory with Applications, ISBN: 978-0-12-372487-8
LANG, Serge, Algebraic Number Theory, ISBN: 0-387-94225-4
NATHANSON, Melvyn B. Elementary Methods in Number Theory, ISBN: 0-387-98912-9
PHILLIPS, BUTTS y SHAUGHNESSY, Álgebra con Aplicaciones, ISBN: 968-6034-93-5
SWOKOWSKI y COLE, Álgebra y Trigonometría con Geometría Analítica, ISBN: 968-7529-26-1
TATTERSALL, James T., Elementary Number Theory in Nine Chapters, ISBN: 0-521-61524-0
APOYO INTERNET
http://es.wikipedia.org/wiki/Ley_de_reciprocidad_cuadr%C3%A1tica
http://es.wikipedia.org/wiki/Residuo_cuadr%C3%A1tico
http://hojamat.es/sindecimales/congruencias/diccio/diccong.htm
http://www.akiti.ca/Mathfxns.html (Solución de ecuaciones)
http://www.famaf.unc.edu.ar/publicaciones/documents/serie_c/CMat31-3.pdf
http://www.vadenumeros.es/actividades/division-por-ruffini.htm (Programa matemático)
http://www.vadenumeros.es/actividades/division-por-ruffini.htm (Soluciones Ruffini)
http://www.wolframalpha.com/examples/ (Programa matemático)
http://www.wolframalpha.com/examples/ (Soluciones algebraicas)
FECHA DE PASCUA: APOYO INTERNET
http://www.divvol.org/recursos/fecha_pascua.htm (Calcula la fecha de Pascua)
http://www.huevosdepascuas.com.ar/Historia/historia_de_la_pascua_catolica.htm
http://es.wikipedia.org/wiki/Pascua
http://www.statveritas.com.ar/Liturgia/La%20Pascua%20de%20Resurreccion.htm
18