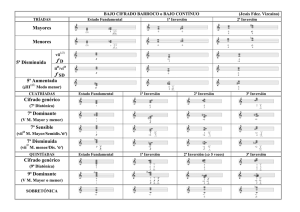
Conceptos básicos de la teoría de la información y de la
Anuncio

Conceptos básicos de la teoría de la información y de la
teoría de la complejidad
Conceptos básicos de la teoría de la información y de la teoría
de la complejidad
José M. Sempere
Departamento de Sistemas Informáticos y Computación
Universidad Politécnica de Valencia
Tipos de seguridad
Teoría de la información
1.
Tipos de seguridad.
2.
Teoría de la probabilidad y criptografía
3.
Concepto de entropía. Propiedades.
4.
Claves falsas y distancia de unicidad.
Teoría de la complejidad
1.
Algoritmos deterministas y no deterministas.
2.
Reducciones entre problemas. Completitud.
3.
Algunas clases de complejidad.
4.
Algunos problemas !"-completos.
5.
Sistemas Interactivos de Demostración.
6.
Aplicación a la criptografía.
Teoría de la probabilidad
Variables independientes
Seguridad computacional
Teoría de la complejidad
Seguridad incondicional
Teoría de la información
p(x,y) = p(x)p(y)
Probabilidad condicional y conjunta
Tipos de ataques
p(x,y) = p(x|y)p(y)
p(x,y) = p(y|x)p(x)
•
•
•
•
Sólo texto cifrado (ciphertext-only)
Texto conocido (known plaintext)
Texto elegido (chosen plaintext)
Texto cifrado elegido (chosen ciphertext)
Teorema de Bayes (regla de Bayes)
p(y|x)p(x)
p(x|y) =
p(y)
Probabilidad y criptografía
Posibles textos sin cifrar :
!
Privacidad perfecta (secreto perfecto)
Posibles claves : " p#(k)
p!(x)
Un criptosistema tiene privacidad perfecta (secreto perfecto) si
Posibles textos cifrados con una clave k∈
∈" : C(k) = { ek(x) : x ∈! }
Probabilidad de aparición de un texto cifrado y ∈ # : PC ( y) =
(∀
∀ x ∈ !) ( ∀ y ∈ #) P!(x|y)= P!(x).
∑ p (k) p (d ( y))
k
{k: y∈C ( k )}
p
k
Probabilidad de aparición del texto cifrado y dado el texto sin cifrar x :
pc ( y | x ) =
∑ p (k )
k
{ k :x = d k ( y )}
Probabilidad de que un texto sin cifrar sea x dado que el texto cifrado sea y :
p p ( x| y ) =
p p ( x ) pc ( y | x )
pc ( y )
pp ( x)
=
∑ p (k )
x
{k :x = d k ( y )}
∑ p (k ) p
k
{k : y ∈C ( k )}
p
Ejemplo Un criptosistema con privacidad perfecta.
! = {a,b}
P!(a) = 0.25
P!(b) = 0.75
" = { k1, k2, k3 } P"(k1) = 0.5 P"(k2) = P"(k3) = 0.25
# = { 1,2,3,4 }
Funciones de encriptamiento ek
Comprobación de que el texto cifrado 3
tiene secreto perfecto :
a
b
k1
1
2
k2
2
3
k3
3
4
1. Calcular p#(i|j) donde i ∈#, j ∈!
2. Calcular p#(i) donde i ∈#
3. Calcular p!(j|i) donde i ∈#, j ∈!
4. Comprobar si se cumple el caso
(∀
∀ x ∈ !) ( ∀ y ∈ #) P!(x|y)= P!(x).
( d k ( y ))
El sistema de Vernam
(Vernam One-time Pad)
Entropía
n
Sea n ≥ 1 y !$= # = " = (%2)n.
Tomamos k ∈ (%2)n y se define la función de cifrado
ek(x) = (x1 + k1 , ... , xn + kn) mod 2
La función de descifrado se define como
H ( X ) = −∑ p ( X = xi ) log 2 p ( X = xi )
i =1
H ( X | y ) = −∑ p ( x | y ) log 2 p ( x | y )
x
H ( X | Y ) = −∑∑ p ( y ) p ( x | y ) log 2 p ( x | y )
y
dk(y) = (y1 + k1 , ... , yn + kn) mod 2
x
Teorema. H(X,Y) ≤ H(X) + H(Y)
H(X,Y) = H(X) + H(Y) sii X e Y son independientes
El sistema de Vernam proporciona privacidad perfecta.
La cantidad de claves utilizadas debe ser igual a la de textos a transmitir (es
altamente vulnerable a un ataque de texto conocido ya que la clave se calcula como la
OR-exclusiva entre y y x).
Teorema. H(X,Y) = H(Y) + H(X |Y) = H(X) + H(Y | X)
Corolario. H(X | Y) ≤ H(X)
H(X | Y) = H(X) sii X e Y son independientes
Claves falsas y distancia de unicidad (I)
H ( K | C ) = − ∑ ∑ p( k , c ) log 2 p( k | c )
Equivocación de clave
c ∈C k ∈K
Entropía de un lenguaje L
Redundancia de un lenguaje L
H(Pn )
H L = lim
n→∞
n
RL = 1 −
HL
log 2 | P|
Claves falsas y distancia de unicidad (II)
sn =
Número de claves falsas en promedio
Teorema
Si |#$| = |!$| y
pK ( k ) =
1
| K|
∑ p( y ) | K ( y )| - 1
y ∈C n
entonces sn ≥
| K|
−1
| P|nRL
Distancia de unicidad n0
log 2 | K |
RL log 2 | P|
n0 ≈
Claves consistentes con un texto cifrado y
K ( y ) = {k ∈ K | ∃x ∈ P n , p P n ( x ) > 0, ek ( x ) = y}
Algoritmos no deterministas
Un ejemplo: El Problema del Viajante de Comercio
C
Sea S una estructura de soluciones para el problema P
10
6
distancia máxima : B
12
6
17
Un algoritmo A no determinista que resuelva P se basa en
dos fases:
A
8
Sea P un problema con un conjunto de restricciones R
B
F
11
E
14
D
25
Estructura de soluciones S : lista de vértices
(1) Fase de conjetura : Conjetura(P,S)
Genera aleatoriamente una permutación de {A,B,C,D,E,F}
y la almacena en S = { v1, v2, v3, v4 ,v5 ,v6 }
(1) Fase de conjetura
Conjetura(P,S)
(2) Fase de verificación : Verifica(S,RP)
(2) Fase de verificación
|S |−1
Verifica(S,R)
Medida de la complejidad
Comprobar si
∑ peso(v , v
i =1
i
) + peso(v|S | , v1) ≤ B
i +1
Un ejemplo de reducción : CH ≤P VC
Reducciones entre problemas. Completitud.
A
Dados dos problemas A y B, diremos que A se reduce a B
(A ≤P B) si existe una función f tal que
C
B
1. f es calculable en tiempo polinómico
2. La instancia x tiene solución en A ⇔ f(x) tiene solución en B
Dado un conjunto de problemas C, diremos que un problema A
es ...
• C-duro si todos los problemas de C se reducen a A
• C-completo si A ∈ C y A es C-duro
• coC si su problema complementario pertenece a C
E
D
A
1
Viajante de Comercio
La distancia máxima se establece
como |V|
1
C
1
Un Circuito Hamiltoniano consiste
en un circuito que recorre todos los
vértices una única vez
2
2
B
1
2
2
E
1
1
D
Algunos problemas NPNP-completos
Algunas clases de complejidad
El problema del Viajante de Comercio
EXPTIME
PSPACE
coNPcoNP-completo
C
NPNP-completo
A
8
10
12
6
6
17
E
B
F
11
B distancia máxima
14
D
25
coNP
P
NP
P : Problemas que admiten algoritmos deterministas polinómicos
NP : Problemas que admiten algoritmos no deterministas polinómicos
PSPACE : Problemas que necesitan espacio polinómico
EXPTIME : Problemas que necesitan tiempo exponencial
“Dados un conjunto de ciudades y las posibles distancias
entre ellas. Dada una distancia máxima B. ¿ Es posible
establecer un tour que recorra todas las ciudades una
sola vez y que no exceda en su distancia a B ?”
Algunos problemas NPNP-completos
Algunos problemas NPNP-completos
El problema de la SATisfacibilidad
El problema de la isomorfía de subgrafos
G1
U = { u1, u2, ..., un } (variables)
G2
A
6
(cada variable uj origina dos literales: uj y uj)
3
C
B
F
1
5
E
2
4
D
C = {c1, c2, ... , cm } (cláusulas)
(cada cláusula es una disyunción de literales)
Ejemplo: C = { {u1 , u2 , u3} , {u2 , u3} , {u4} , {u1 , u3 , u4} }
“Dados dos grafos G1 y G2. ¿ Existe un subgrafo de
G1 isomorfo a G2 ?”
Algunos problemas NPNP-completos
El problema de las incongruencias simultáneas
C = { (a1,b1), (a2,b2), ... , (an,bn) }
ai , bi son enteros positivos
ai ≤ bi para cualquier valor de i
“Dado el conjunto C. ¿ Existe un valor entero x tal que
x ≡ ai (mod bi) para 1 ≤ i ≤ n ?”
“Dados los conjuntos U y C. ¿ Existe una asignación a
las variables de U que haga ciertas todas las cláusulas
de C simultáneamente ?”
Algunos problemas NPNP-completos
El problema de las congruencias cuadráticas
a , b y c son enteros positivos
“Dados a, b y c. ¿ Existe un valor entero positivo x < c
tal que x2 ≡ a (mod b) ?”
El problema se puede resolver en P si el entero
b es primo (asumiendo algunas condiciones de
partida)
Un ejemplo de demostración interactiva: No isomorfía de grafos (I)
Sistemas Interactivos
mensajes P-a-V
Demostrador
(prover)
P
x
Verificador
(verifier)
V
Generador
aleatorio
entrada
mensajes V-a-P
A
B
C
D
1
3
4
2
Grafos isomorfos:< A,1> <B,3> <C,4> <D,2>
A
B
C
D
1
3
• La computación se establece por turnos (rounds) que comienza V
• La aceptación o rechazo de la entrada la establece V
• El número de mensajes y la longitud de los mismos están acotados
polinómicamente en relación con la longitud de la entrada
Un ejemplo de demostración interactiva: No Isomorfía de grafos (II)
Pregunta: Dados dos grafos G1 y G2 ¿ Son no isomorfos ?
•El problema de la no isomorfía de grafos pertenece a
coNP.
coNP (su problema complementario pertenece a NP)
NP
•Hasta el momento no existe ninguna evidencia de su
posible pertenencia a NP.
NP
•Existen subconjuntos del problema que pertenecen a
P (i.e. grafos planares)
2
4
Grafos no isomorfos
Un ejemplo de demostración interactiva : NoIsoGraf
Instancia: G1=(V1,E1) y G2=(V2,E2)
V : m = random{1,2}
Gn = random(Gm)
V-a-P : <Gn>
P : Comprueba qué grafo es isomorfo a Gn y asigna su
índice a p. Si ambos grafos son isomorfos a Gn entonces
selecciona p = random{1,2}
P-a-V : <p>
V : Si p ≠ m entonces rechaza la instancia. Si p = m acepta.
Si G1 y G2 son isomorfos entonces P no tiene opción de
establecer con qué grafo se corresponde Gn y la probabilidad
de equivocarse es de 0.5
Repitiendo dos veces el experimento la probabilidad pasa a ser
0.25
Sistemas Interactivos con conocimiento cero (nulo)
mensajes P-a-V
Demostrador
(prover)
P
x
Verificador
(verifier)
V
Generador
aleatorio
entrada
mensajes V-a-P
Un Sistema Interactivo decimos que presenta conocimiento cero
si la información que envía P a V puede ser simulada aleatoriamente
(P no desvela ninguna información acerca de la entrada)
Aplicaciones de la Teoría de la Complejidad a las
técnicas criptográficas
•
•
•
Todos los problemas NPNP-completos presentan instancias fáciles
de resolver.
Toda instancia fácil de resolver puede enmascararse como una instancia
difícil.
El problema de desenmascarar la instancia se resuelve a partir de una
información secreta (clave)
Aplicación a los sistemas asimétricos o de clave pública
• Los Sistemas Interactivos con conocimiento cero definen protocolos
criptográficos útiles para la autentificación y la firma digital