Taller 1 – Clase 6

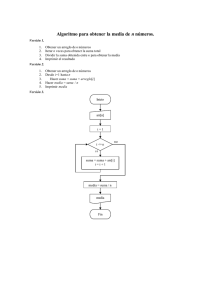
CLASE 7:MATRICES (REP)
C8
6
7. MATRIZ
Matriz es un tipo de memoria que sirve para almacenar un grupo de valores a través del uso de filas y columnas. 7.1. FORMATO
Dimensionar Nombre(fila, columna)
O
Vector Nombre(fila, columna)
Dimensionar Matriz k(4,5)
O
Matriz K(10,25)
7.2. CONVENCION
CLASE
Los ejercicios que indiquen “que ya están cargados” significa que no hace falta realizar el algoritmo de carga, para diferenciar en el momento de definir si se esta creando o ya esta cargado colocaremos un subrayado sobre la instrucción de acuerdo a la siguiente tabla: Cuando la instrucción dice Significa MATRIZ
Matriz G(3,4) Significa que la matriz se esta creando, no tiene valores dentro de la matriz. Matriz H(5,7) Significa que la matriz esta cargado con valores dentro. 7.3. CONVENCIONES DE FORMATO DE MATRICES
Fila inferior
Columna inferior
46
47
03/08/2015 15:00
Fila superior
Columna diagonal
principal
Columna diagonal
secundaria
Columna superior
Matriz Cuadrada
Triangula inferior y
superior
CLASE 7:MATRICES (REP)
Matrices
38.
7.4. EJERCICIOS RESUELTOS
Nº
36.
Nº
Algoritmo
1
2
3
4
5
6
7
8
9
10
11
12
13
Algoritmo
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Crear una matriz de tamaño 3 por 4 y cargarla.
Explicación
INICIO
Matriz K(3,4)
F=0, A=0
Mientras F < 3
C=0
Mientras C < 4
Leer A
K(F,C)=A
C=C+1
FinMientras
F=F+1
FinMientras
FIN
Nº
Hallar la sumatoria de los valores pares de una matriz N(6,7)
Algoritmo
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
48
INICIO
MATRIZ N(6,7)
F=0, S=0
Mientras F < 6
C=0
Mientras C < 7
Si N(F,C)/2 = ENT(N(F,C)/2)
S= S + N(F,C)
FinSi
C=C+1
FinMientras
F=F+1
FinMientras
Imprimir S
FIN
Explicación
Nº
Teniendo una matriz K(5,5) imprimir la sumatoria de la diagonal
principal
Algoritmo
1
2
3
4
5
6
7
8
10
11
12
13
14
15
16
17
49
Explicación
INICIO
MATRIZ G(8,5)
F=0, MA= G(0,0)
Mientras F < 8
C=0
Mientras C < 5
Si G(F,C) > MA
MA = G(F,C)
FinSi
C=C+1
FinMientras
F=F+1
FinMientras
Imprimir MA
FIN
39.
37.
Dada una matriz G(8,5) hallar el mayor valor.
INICIO
Matriz K(5,5)
F=0, S=0, SDP=0
Mientras F < 5
C=0
Mientras C < 5
Si C=F
SDP = SDP + K(F,C)
FinSi
C=C+1
FinMientras
F=F+1
FinMientras
Imprimir SDP
FIN
03/08/2015 15:00
Explicación
CLASE 7:MATRICES (REP)
Matrices
40.
Nº
Dada una matriz L(4,4) sumar las filas inferiores y contar
cuantos pares existe en filas superiores.
Algoritmo
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
41.
Nº
50
103.Dada una matriz V(4,5) imprima cuantos elementos son impares.
104.Dada una matriz V(15,18) imprima cuantos múltiplos de 3 existen en la
primera fila (g4).
105.Dada una matriz P(6,6) hallar la sumatoria de la columna inferior y la
cantidad de pares en las columnas superiores. (g2)
106.Dada una matriz F(3,3) imprima si existe valores impares dentro de la
matriz.
107.Dada una matriz cuadrada k(5,5) sumar los valores de la diagonal
secundaria. (G1).
Se tiene una matriz cuadrada de tamaño B(4,4) cargada, diga
cuantas filas se necesita para hallar una sumatoria mayor que 30
Algoritmo
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Explicación
INICIO
Matriz L(4,4)
F=0, SINF=0, CPSUP=0
Mientras F < 4
C=0
Mientras C < 4
Si F < 2
SINF = SINF + L(F,C)
Sino
Si L(F,C)/2 = ENT
(L(F,C)/2)
CPSUP = CPSUP + 1
FinSi
FinSi
C=C+1
FinMientras
F=F+1
FinMientras
Imprimir SINF , CPSUP
FIN
7.5. EJERCICOS PROPUESTOS
Explicación
INICIO
MATRIZ M(4,4)
F=0, S=0
Mientras F < 4
C=0
Mientras C < 4
S= S + M(F,C)
C=C+1
FinMientras
Si S > 30
Imprimir F
F=B
FinSi
F=F+1
FinMientras
FIN
51
03/08/2015 15:00
CLASE 7:MATRICES (REP)
Matrices
7.7.2. Operaciones con matrices
7.6. RESPUESTA DE EJERCICIOS PROPUESTOS
g1
g2
INICIO
MATRIZ K(5,5)
F=0, C=4 S=0
Mientras F < 5
S =S+
K(F,C)
F = F+1
C = C-1
FinMientras
Imprimir S
FIN
INICIO
Matriz V(6,6)
F=0, C=0, CP=0 , SINF=0
Mientras F < 6
C=0
Mientras C < 6
Si C < 3
SINF = SINF+ K(F,C)
Sino
Si K(F,C)/3 =
ENT(K(F,C)/3)
CP = CP + 1
FinSi
FinSi
FinMientras
F=F+1
FinMientras
Imprimir SINF, CP
FIN
g3
INICIO
Matriz V(3,3)
F=0, C=0, CI=0
Mientras F < 3
C=0
Mientras C < 3
Si K(F,C)/2 <>
NT(K(F,C)/2)
CI = CI + 1
FinSi
C=C+1
FinMientras
F=F+1
FinMientras
Si CI=0
Imprimir “No hay impares
em
la matriz”
Sino
Imprimir “Hay impares en
la matriz”
FinSi
FIN
g4
g6
INICIO
Matriz V(15,18)
F=0, CM3=0
Mientras F < 15
C=0
Mientras C < 18
Si F=0
Si K(F,C)/3 =
ENT(K(F,C)/3)
CM3 = CM3 + 1
FinSi
FinSi
FinMientras
F=F+1
FinMientras
Imprimir S, CP
FIN
110.Dada una matriz K(6,5), imprima la sumatoria de valores pares.
111.Teniendo una matriz P(X,Y) imprimir si existe mayor sumatoria de los
valores, o iguales o impares.
112.Dada una matriz H(6,8), hallar la sumatoria de valores múltiplos de 3 en
las filas inferiores y la cantidad de múltiplos de 3 en las filas superiores
113.Teniendo una matriz MAT (P,Q), imprimir en qué fila y columna se
encuentra el menor elemento.
114.Dada una matriz Z(10,7), hallar la cantidad de pares e impares en las
filas superiores.
115.Dada una matriz B(7,7) imprima donde se encuentra mas pares en la
diagonal principal o en la diagonal secundaria.
116.Teniendo una matriz N(X, Y). Hallar donde se encuentra el mayor
elemento, en fila superior o fila inferior. Las filas son siempre pares.
117.Dado una matriz k(5,9), hallar el mayor valor de la diagonal principal.
7.8. EJERCICIOS DESAFIO
INICIO
MATRIZ K(15,18)
F=0, C=0, CM3 = 0
Mientras C < 18
Si K(F,C)/3 =
ENT(K(F,C)/3)
CM3 = CM3 + 1
FinSi
C = C+1
FinMientras
Imprimir CM3
FIN
118.
Dada una matriz H(8,5) hallar el menor valor de las filas superiores.
119.
Dada una matriz H(6,8), imprima que se encuentra primero el mayor o
el menor (El control se realiza de fila a fila).
120.
Dada una matriz G(5,8) imprima hay valores que se repiten en la
matriz.
121.
Dada una matriz H(4,3), imprima si el valor mayor se repite o no en la
matriz.
7.7. EJERCICIOS PARA REALIZAR
7.7.1. Carga de Matrices
108.
Teniendo una matriz 3 x 3. Imprimir cuantos elementos son pares.
109.
Crear una matriz de tamaño 6, 8. Cargar con el valor 35 todas las
columnas impares.
52
53
03/08/2015 15:00