Raíces complejas múltiples de D(s)
Anuncio

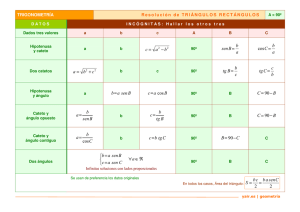
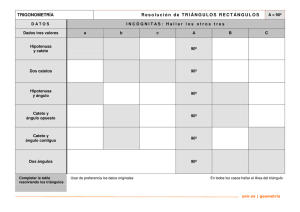
3.4 Raíces complejas múltiples de D(s) Las raíces complejas repetidas se manejan igual que las raíces reales repetidas. La única diferencia es que el álgebra implica números complejos. Por ejemplo: F ( s) = (s 768 2 + 6s + 25 ) 2 Si descomponemos el denominador en sus raíces: F (s) = 768 (s + 3 − j 4 ) (s + 3 + j 4 ) 2 2 = K1 K2 K1* K 2* + + + 2 2 (s + 3 − j 4) (s + 3 − j 4 ) (s + 3 + j 4 ) (s + 3 + j 4 ) Solo tenemos que evaluar K1 y K2 ya que K1* y K 2* son complejos conjugados respectivamente. El valor de K1 es: K1 = y y K2 = 768 (Hacer os ejercicios 16.15) 768 = −12 768 2(768 ) d =− 2 ds (s + 3 + j 4 ) s = −3 + j 4 (s + 3 + j 4 )3 K1* = −12 F (s) = y su transformada inversa: = (s + 3 + j 4)2 s = −3+ j 4 ( j8)2 = s = −3 + j 4 2(768 ) = − j 3 = 3 − 90º ( j8)3 K 2* = j 3 = 3 90º − 12 + − 12 (s + 3 − j 4 )2 (s + 3 + j 4 )2 + 3 − 90º s + 3 − j4 f (t ) = −24te −3t cos 4t + 6e −3t cos(4t − 90º ) + 3 90º s + 3 + j4