“Empezamos a conocer

Estadística Descriptiva
Guía de autoaprendizaje
Estadística
Descriptiva
Modalidad de Educación Abierta y
a Distancia
Rita Oliva Maya Hernández
Secretaría de Educación Pública
Dirección General de Educación Superior
Escuela Nacional de Biblioteconomía y
Archivonomía
México 1998
Estadística Descriptiva
39
Secretaría de Educación Pública
Subsecretaría de Educación Superior e Investigación Científica
Dirección General de Educación Superior
Escuela Nacional de Biblioteconomía y Archivonomía
Estadística Descriptiva
(Serie guías de autoaprendizaje)
Modalidad de Educación Abierta y a Distancia
Primera edición 1998
ISBN 970-18-0985-8
Impreso en México
Diseño:
Ivonne Bautista Carmona
Portada:
Patricia Vázquez Langle
40
Estadística Descriptiva
“Empezamos a conocer
un fenómeno cuando
somos capaces de medirlo y expresarlo
en números; mientras tanto,
nuestro conocimiento de dicho
fenómeno será deficiente
e insatisfactorio”
Lord Kelvin
41
42
Estadística Descriptiva
ÍNDICE
Presentación
Introducción
7
9
UNIDAD 1 CONCEPTOS BÁSICOS
13
1.1 Definición, objeto y clasificación de la Estadística
16
1.2 Población y muestra
20
1.3 Variables
27
1.4 Escalas de medición
1.4.1 Escala nominal
31
1.4.2 Escala ordinal
32
1.4.3 Escala de intervalo
1.4.4 Escala absoluta
32
31
32
UNIDAD 2 PRESENTACIÓN DE DATOS
39
2.1 Tipos de datos
42
2.1.1 Datos categóricos
2.1.2 Datos ordenados por rango
43
2.1.3 Datos métricos
43
42
2.2 Distribución de frecuencias
46
2.2.1 Simples
47
2.2.2 Para datos agrupados
57
43
UNIDAD 3 REPRESENTACIONES GRÁFICAS
73
3.1 Gráfica de barras
77
3.2 Gráfica de sectores
3.3 Histograma de frecuencias absolutas
86
3.4 Polígono de frecuencias absolutas
92
3.5 Polígono de frecuencias relativas acumuladas u ojiva porcentual
95
UNIDAD 4 ESTADÍSTICA DESCRIPTIVA
109
4.1 Medidas de tendencia central
111
4.1.1 Media
111
4.1.2 Mediana
111
4.1.3 Moda
111
4.2 Medidas de dispersión
127
4.2.1 Rango
127
4.2.2 Cuartiles
127
4.2.3 Desviación media
132
4.2.4 Varianza
138
44
80
Estadística Descriptiva
4.2.5 Desviación estándar
138
4.2.6 Coeficiente de variación
143
4.2.7 Teorema de Chebyshev
145
Resumen de la unidad 1
153
Resumen de la unidad 2
154
Resumen de la unidad 3
155
Resumen de la unidad 4
157
Lecturas
159
45
PRESENTACIÓN
La Biblioteconomía y la Archivonomía son dos profesiones que han
cobrado un fuerte impulso durante los últimos años. Las condiciones
cambiantes que han intervenido en su entorno y que han originado nuevos
problemas y nuevos enfoques en sus campos de aplicación se han debido
principalmente al progreso científico y tecnológico y a la explosión
documental: una mayor producción y explotación de material, un notable
incremento de usuarios y el uso cada vez más intenso de los medios
informáticos y de las telecomunicaciones para el almacenamiento,
organización e intercambio de información.
Esta situación contrasta con la carencia de recursos humanos con una
adecuada preparación académica que permita brindar una atención
profesional a las necesidades que, en materia de información,
constantemente van en aumento entre la sociedad mexicana.
Es por ello que la Escuela Nacional de Biblioteconomía y Archivonomía
(ENBA), como institución de educación superior formadora de profesionistas
especializados en el manejo de la información, ha emprendido la impartición
de sus licenciaturas en la modalidad abierta y a distancia, con el propósito
de ofrecer una cobertura educativa a nivel nacional en ambas
especialidades, coadyuvar en la superación de los rezagos de personal
profesional en las bibliotecas y archivos de México, propiciar la
investigación y la difusión de la cultura bibliotecaria y archivística y participar
activamente en las políticas educativas del gobierno federal manifestadas
en el Programa de Desarrollo Educativo 1995-2000.
La modalidad abierta y a distancia se convierte así en una opción
dirigida a todas aquellas personas formadas con la experiencia pero que
carecen de una preparación académica en las áreas de Biblioteconomía o
de Archivonomía.
En este sentido, se pretende rescatar, valorar, reconocer y acreditar
esa experiencia adquirida a través del tiempo en el entorno laboral de las
bibliotecas y los archivos, utilizando estrategias de aprendizaje que resulten
congruentes con las características de la modalidad. Es decir, para superar
los obstáculos de distancia y las dificultades de tiempo y espacio para el
estudio se recurre a aspectos académicos que generalmente son poco
comunes en la modalidad escolarizada, pero que también persiguen los
mismos propósitos.
46
Estadística Descriptiva
Los materiales didácticos surgen entonces como uno de los soportes
más importantes, junto con las asesorías y los medios de comunicación a
distancia, en los que habrás de sustentar tu formación.
Las guías de autoaprendizaje representan la parte medular de los
materiales didácticos. Son el principal medio de apoyo con el que cuentas
para avanzar en tu proceso de aprendizaje, tomando en cuenta que asumes
una responsabilidad compartida con el asesor y que eres tú quien
determina su propio ritmo de avance. Su contenido se encuentra adaptado
convenientemente a la lógica del problema, de la disciplina y del campo del
conocimiento que se aborda y responde a los elementos didácticos y
comunicacionales que permiten favorecer de mejor manera el estudio
independiente.
En cada asignatura cuentas con una guía de autoaprendizaje y en
muchas de ellas ésta se encuentra complementada con una guía de
lecturas. Esta guía es un material de estudio que contiene lecturas tomadas
de diversos libros que, a juicio del autor de la guía de autoaprendizaje
correspondiente, necesitarás consultar para apoyar tu aprendizaje.
Las asesorías son un medio al que podrás recurrir en cualquier
momento para consultar tus dudas o solicitar sugerencias sobre tus
métodos y hábitos de estudio. Los medios de comunicación a distancia te
permitirán establecer comunicación con los asesores desde cualquier parte
en que te encuentres.
La presente guía representa entonces sólo una pequeña parte del gran
apoyo con el que cuentas, pero constituye también el trabajo colectivo que
la ENBA ha venido desarrollando con el firme propósito de contribuir en tu
formación profesional.
Estamos seguros que harás un correcto uso de ella y que sabrás
aprovecharla adecuadamente.
47
INTRODUCCIÓN
La evolución del uso y manejo de la información ha motivado que
estructuras importantes y vitales como son las de enseñanza modifiquen
sus planes de estudio, y la Escuela Nacional de Biblioteconomía y
Archivonomía no podía ser la excepción, por tal motivo ha instaurado su
Modalidad Abierta y a Distancia con el objeto de impartir las carreras de
Biblioteconomía y Archivonomía y así formar parte activa en el desarrollo
de profesionales de estas áreas.
Dentro de este Sistema se ha creado para ti esta Guía de
Autoaprendizaje como un apoyo para que puedas aprender la materia de
Estadística Descriptiva, la cual forma parte del Plan de Estudios de estas
carreras en su tronco común.
Antes de que inicies tu aprendizaje te invito a conocer los
antecedentes de la materia que nos ocupa.
La historia de la Estadística es extensa, surge como todo lo creado por
el hombre: por la necesidad de conocer y modificar su entorno a fin de
entenderlo. Aunque existen antecedentes de que los chinos efectuaron
censos hace más de 40 siglos y de que en la Biblia se mencionan datos
estadísticos en el Libro de los Números, la etapa moderna, arbitrariamente
elegida se encuentra comprendida en el período 1890-1940.
Es importante destacar que en sus inicios la Estadística se utilizó con
el propósito de interpretar fenómenos biológicos y la conducta social de
grandes masas, un ejemplo de ello son las primeras Tablas de mortalidad
elaboradas por John Graunt (1620-1674) que contenían el número de
nacimientos, matrimonios, bautizos y defunciones, antecedente de las que
hoy se utilizan en los Seguros de Vida.
Actualmente la Estadística es una herramienta importante y necesaria
en todas las áreas del conocimiento ya que permite interpretar los datos
obtenidos a través de investigaciones y en su caso, tomar una decisión que
tenga como fundamento el comportamiento observado y analizado.
Como verás, los antecedentes de la Estadística o Métodos
Estadísticos como algunos le llaman, resultan bastante interesantes y en tu
caso, en el área de la cual ya formas parte como estudiante de la
información es de vital importancia que los manejes y apliques en la
solución de problemas.
48
Estadística Descriptiva
Una de las ventajas que tiene el uso de esta herramienta en el campo
laboral de estas dos profesiones es la facilidad de poder manipular grandes
cantidades de datos que al ser analizados en forma manual o a través de
una computadora permiten obtener indicadores específicos ya sea para
conocer la satisfacción de un servicio, el promedio de la carga de trabajo e
inclusive para planear el crecimiento de volúmenes, costos, etc., en cierta
área, permitiendo realizar planes de expansión para el futuro.
Es preciso hacer notar que se debe tener cuidado al hacer uso de la
Estadística, ya que la presentación de datos equivocados puede provocar
una falsa interpretación y como consecuencia llegar a una conclusión
errónea. Es de suma importancia mencionar que la interpretación es la base
fundamental del uso de esta herramienta.
Algunas recomendaciones que te hago con el propósito de facilitarte la
comprensión y manejo adecuado de las unidades que integran esta
asignatura son que revises cuidadosamente el material que se te presenta
en cada tema, leas las instrucciones de cada actividad y las ejecutes
tomando en cuenta lo aprendido, sin perder de vista tu experiencia previa
que es muy valiosa y que te ayudará a apropiarte de la información nueva
que aquí se te presenta.
No olvides que el éxito para lograr la meta que te has propuesto lo
alcanzarás a través del estudio y del trabajo que se te solicita en actividades
a desarrollar en cada tema, retroalimentándote de tal forma que tú mismo
tengas conciencia del progreso que obtienes cada día que te esfuerzas.
Adelante, tú puedes.
Al término de cada unidad encontrarás un resumen de los conceptos
más importantes que espero te sea de gran utilidad para que reflexiones
sobre lo aprendido antes de contestar la EVALUACIÓN que debes enviar a
tu asesor una vez que la hayas resuelto correctamente y en su totalidad.
Tu calificación final será el resultado de considerar:
4 evaluaciones de aprendizaje (una por unidad), las cuales cuentan un
40% y una evaluación final que tiene un valor del 60%.
Para la mejor comprensión del objetivo es necesario reiterar una vez
más que el uso adecuado de la Estadística es básico en cualquier campo
de la investigación, es por ello que los conocimientos que adquieras en esta
asignatura te servirán de apoyo para el mejor desarrollo de temas incluidos
en otras materias de la carrera ya sea si estudias Archivonomía, o si te
49
encuentras cursando la carrera de Biblioteconomía y en general en todas
aquellas donde se requiera la representación de datos de tal forma que su
interpretación correcta permita la mejor toma de decisiones.
EL OBJETIVO GENERAL de esta asignatura es proporcionarte los
elementos fundamentales necesarios para elaborar tablas de distribución de
frecuencias y gráficas, así como calcular medidas descriptivas, todo lo cual
te permitirá reconocer la importancia de la estadística en los procesos de
planeación, toma de decisiones, administración y medición del
comportamiento de los servicios ofrecidos en los campos bibliotecario y
archivístico.
Esta guía contempla 4 unidades:
1.- CONCEPTOS BÁSICOS
2.- PRESENTACIÓN DE DATOS
3.- REPRESENTACIONES GRÁFICAS
4.- ESTADÍSTICA DESCRIPTIVA
Iniciamos la primera unidad con los conceptos básicos de la
asignatura, para continuar con la presentación de datos, posteriormente se
te indicará el procedimiento a seguir para obtener su representación gráfica.
En la unidad 4 calcularás los valores centrales de una muestra o población
así como las medidas que te indican el grado de dispersión entre sus
elementos.
Al principio de cada unidad se te pide contestar algunas preguntas que
integran el DIAGNÓSTICO, las cuales permitirán identificar tus ideas
previas sobre la misma, haciendo una breve REFLEXIÓN que despejará tus
dudas y te preparará para el desarrollo de los temas, cada uno de ellos
contiene una sección de actividades denominada ¿QUÉ HE APRENDIDO?
que te retroalimentará a través de preguntas y/o problemas que debes
resolver en el espacio correspondiente.
Para que te familiarices con las unidades de esta asignatura, echa un
vistazo al índice; una vez que conozcas los temas que se desarrollarán, es
necesario que reflexiones y contestes la siguiente pregunta:
¿Cuáles son tus expectativas sobre el aprendizaje del contenido que
se te ha planteado?
________________________________________________________
____________________________________________________________
_______________
50
Estadística Descriptiva
Espero que todo lo que hasta aquí has conocido te motive para
continuar y además, cubra tus expectativas, ya que como tú lo irás
descubriendo, el mundo de la Estadística es realmente excitante. Avanza
firmemente para que llegues a la meta, tú puedes.
51
52
Estadística Descriptiva
UNIDAD 1
CONCEPTOS BÁSICOS
En esta primera unidad, tú como estudiante deseoso de conocer los
conceptos más usados en esta asignatura tendrás a tu alcance una breve
definición de cada uno de ellos, este conocimiento debe ser
complementado con tus actividades de aprendizaje a fin de que en lo
sucesivo seas capaz de identificarlos y manejarlos adecuadamente.
¿QUÉ VOY A APRENDER EN ESTA UNIDAD?
A definir e identificar los conceptos básicos elementales que se utilizan
en Estadística.
Para conocer tus ideas previas sobre cada uno de los temas a
desarrollar en esta guía, es necesario que antes de iniciar las unidades
contestes lo que se te solicita en el Diagnóstico, el cual forma parte
importante en tu formación ya que por medio de el estaremos en posibilidad
de recuperar tu experiencia previa y prepararte para la apropiación de
conocimientos nuevos.
53
DIAGNÓSTICO
1) Escribe el significado que tiene para ti la palabra Estadística.
________________________________________________________
____________________________________________________________
______________
2) Recorta, lee y pega cualquier artículo de un periódico reciente que
contenga gráficas y destaca los términos estadísticos que contenga.
3) Anota algunos de los mensajes que ves en televisión en donde
consideres que se están utilizando conceptos de estadística.
________________________________________________________
____________________________________________________________
_______________
4) Busca en el diccionario el significado de la palabra inferir y anótalo.
________________________________________________________
____________________________________________________________
_______________
54
Estadística Descriptiva
Si al realizar las actividades del
diagnóstico advertiste que
desconoces el significado de la palabra Estadística, no te preocupes, en
seguida podrás leer una breve definición:
“La palabra Estadística está relacionada con la palabra “estado”, y originalmente la actividad llamada
estadística fue una clase sistemática de ciencia política comparada. Esta actividad se centró gradualmente en
tablas numéricas de hechos económicos, demográficos y políticos, y así “estadística” vino a significar la
recopilación y análisis de tablas numéricas”
Tanto en la lectura del artículo que se te solicitó, como en los mensajes
televisados, encontraste términos utilizados en la Estadística como son: “se
ha demostrado estadísticamente”, “estadísticas relativas a”, “proporción”,
“por ciento”, “en base a los datos obtenidos se infiere que...” entre otros,
todos ellos nos muestran su utilidad en el mundo actual en que vivimos ya
que nos auxilian a planear y obtener información de diversos fenómenos a
fin de organizarla y analizarla para predecir a partir de lo calculado (inferir) y
llegar a conclusiones que nos permitan tomar decisiones.
Es muy importante que recuerdes el significado de inferir: “inducir o
predecir a partir de ciertos resultados”.
Muy bien, ahora que ya tienes idea de lo que se puede realizar
utilizando como herramienta la estadística iniciaremos nuestro aprendizaje
formal.
55
1.1 DEFINICIÓN, OBJETO Y CLASIFICACIÓN DE LA
ESTADÍSTICA
Actualmente, la Estadística se utiliza en todas las áreas, no hay ciencia
que no la use o profesión que no la aplique, ya que los métodos que
desarrolla se manejan en todos los campos porque permiten describir la
información recopilada por diversos medios, haciéndola más accesible a fin
de poder analizarla e interpretarla fácilmente.
Es preciso hacer notar que la Estadística es una rama de la
Matemática aplicada, razón por la cual se requiere manejar ciertos
conceptos sobre la materia, que en su momento se te explicarán
brevemente así como la notación correspondiente.
La utilidad que tienen los métodos estadísticos en diversas áreas es
quizá el motivo por el cual existen múltiples definiciones de Estadística
como las que se te presentan a continuación y que se te sugiere leer con
detenimiento, SUBRAYANDO las palabras que consideres más importantes
en cada una.
Robert Johnson escribe: Estadística es la ciencia de recolectar,
clasificar, describir e interpretar datos numéricos.
Para Enrique Portilla Chimal la Estadística o Métodos Estadísticos son
los métodos que se aplican a la recolección, organización, presentación,
análisis e interpretación de datos numéricos.
Luis Magaña Cuéllar indica:
Estadística es un conjunto de
procedimientos que sirven para organizar y resumir datos, hacer inferencias
a partir de ellos y transmitir los resultados de manera clara, concisa y
significativa.
William Mendenhall explica “El objetivo de la Estadística es hacer
inferencias (predicciones) acerca de una población (total de datos), sobre la
base de la información contenida en una muestra (parte de la población)”
para ello afirma que como principio se debe tener un problema estadístico el
cual debe contener 6 elementos donde los primeros 3 se analizan a través
de la Estadística Descriptiva y los 3 restantes con la Estadística Inferencial.
A continuación se describen:
1) Definición clara del conjunto de datos de interés.
56
Estadística Descriptiva
Conocer el problema e identificar las preguntas claves de la
investigación: ¿Qué quiero?
2) Diseño del experimento, considerado éste como un proceso por
medio del cual se obtiene un dato.
Procedimiento para elegir la muestra adecuada que permita contestar
las preguntas planteadas y extraer la información que se requiere de la
población.
3) Manejo de la información.
Los datos obtenidos se ordenan, se presentan en tablas estadísticas,
se calculan medidas que informen sobre el comportamiento de los mismos y
se elaboran gráficas.
4) Análisis de los datos.
Identificación del procedimiento para hacer inferencias sobre el total de
datos con base en la información que proporciona una parte de ellos.
5) Obtención de una medida que muestre qué tan confiable es la
inferencia a la que se llegó.
6) Conclusiones y toma de decisiones.
De todo lo anterior se desprende entonces que el objeto de la
Estadística es obtener, organizar y resumir información en tablas y gráficas
que al mismo tiempo que describan la forma en que se comportan los datos,
también faciliten el cálculo de parámetros o estadísticos, esto es, números
que describan las características de una categoría que agrupa elementos
comunes con respecto a una población o a una muestra según sea el caso.
La Estadística para su estudio se clasifica en Estadística
Descriptiva o Deductiva y Estadística Inferencial o Inductiva. En la
siguiente tabla se observan claramente las partes que integran cada
división:
57
DESCRIPTIVA O DEDUCTIVA
Incluye las fases de:
-Obtención de datos a través de encuestas o investigaciones de campo
-Organización de los mismos (orden ascendente o descendente si son
numéricos) y conteo
-Presentación de la información en cuadros y/o tablas
-Gráficos que muestren el comportamiento de la información
-Cálculo de medidas descriptivas (media, moda, mediana, etc.)
ESTADÍSTICA
INFERENCIAL O INDUCTIVA
Contempla los métodos que permiten:
- Generalizar a partir de los valores calculados con técnicas descriptivas
- Obtener conclusiones
- Tomar decisiones
DEDUCTIVA: Parte de lo general para llegar a lo particular
INDUCTIVA: Considera lo particular para generalizar
Claramente se puede observar en la tabla que ambas divisiones se
complementan ya que por medio de la Estadística Descriptiva es posible
obtener información que se organiza, presenta y describe en forma
numérica para posteriormente, a través de la Estadística Inferencial
generalizar y tomar decisiones teniendo como soporte la información que se
obtuvo a través de la primera. Cabe hacer mención de que el proceso de
interpretar los datos no es infalible.
¿QUÉ HE APRENDIDO?
Es de suma importancia que evalúes tus conocimientos, verifiques tu
avances y planifiques tu aprendizaje, para ello debes participar
ACTIVAMENTE desarrollando lo que se te solicita. Por favor, no continúes
si tienes dudas o errores en tus respuestas.
1) De las definiciones de Estadística que se te han presentado, elabora
una relación de las palabras comunes a todas.
58
Estadística Descriptiva
________________________________________________________
____________________________________________________________
_______________
2) Utilizando los términos escritos en el anterior inciso, escribe tu
propia definición de Estadística.
________________________________________________________
____________________________________________________________
_______________
3) Acude con un Bibliotecario o Archivónomo dentro de tu localidad y
pregúntale en qué aspectos de las tareas que se realizan en su profesión
aplica la Estadística. Anota su respuesta, el lugar al que acudiste y la
profesión de la persona que contestó tus preguntas.
________________________________________________________
____________________________________________________________
____________________________________________________________
____________________________________________________________
_______________________________
4) Anota como mínimo 3 disciplinas en donde se aplique la Estadística
y describe brevemente un ejemplo en cada una de ellas.
________________________________________________________
____________________________________________________________
____________________________________________________________
____________________________________________________________
____________________________________________________________
____________________________________________________________
_______________________________________________
59
1.2 POBLACIÓN Y MUESTRA
POBLACIÓN TAMAÑO N
MUESTRA TAMAÑO
n
La POBLACIÓN Estadística se encuentra formada por un conjunto de
personas, entidades u objetos bien definidos, del cual se quiere saber algo
que nos interesa, el número total de elementos que la forman, llamado
tamaño de la población, se denota con la letra ene mayúscula “N”.
Existen 2 tipos de población:
Finita: {a, e, i, o, u}.
Formada por un número limitado de observaciones, por ejemplo
las vocales, el número total de libros que existen en una biblioteca o el
número de investigadores que acuden a un archivo en un período
determinado.
Infinita: {1, 2, 3, 4, ... ∝ }
Contiene un gran conjunto de medidas u observaciones que no
pueden alcanzarse por conteo, es decir, se puede numerar el primer
elemento pero no el último como el conjunto de los números Naturales,
el número de expedientes que contienen la Historia de México o el
número de libros impresos.
MUESTRA REPRESENTATIVA o MUESTRA es un subconjunto de la
población de interés donde el número de datos es menor que el de la
población. En este caso el tamaño de la muestra se simboliza con la letra
ene (n) minúscula. Una muestra del número total de libros que existe en
una biblioteca puede estar formada por los volúmenes de una asignatura,
en un Archivo la muestra puede ser un cierto número de expedientes que
se refieran a un tema en común.
60
Estadística Descriptiva
En caso de contar con el total de datos de una población es posible
calcular sus parámetros o características medibles como el promedio o la
proporción entre una categoría y el total de datos obtenido; sin embargo, si
se trata de una población infinita la estimación de un parámetro de la misma
se realiza a través de la información que proporciona la muestra con los
llamados estadísticos o estadígrafos, los cuales también son
características medibles.
Parámetro
POBLACIÓN
(tamaño N)
MUESTRA
(tamaño n)
Estadístico
Un parámetro es para una población lo que un estadístico para una
muestra.
Es necesario aclarar que no cualquier muestra es adecuada para fines
estadísticos, se debe tener en cuenta que la muestra con la que se
realizarán cálculos reproduzca en lo posible los rasgos generales de la
población, para ello se tiene que considerar lo siguiente:
- Los elementos se deben escoger en forma aleatoria, esto es al azar.
Para ilustrar el término aleatorio o al azar, consideremos el siguiente
ejemplo: Si de un grupo de 10 personas se quiere escoger aleatoriamente a
3, a cada una se le asigna un número y sin relacionar dicho número con la
persona se selecciona cualquier terna que puede ser: 1, 3, 8 ó 2, 5, 10, etc.
- Cada elemento de la población debe tener la misma oportunidad de
ser escogido.
A los valores de los parámetros se les conoce con el nombre de
valores verdaderos. Uno de los parámetros más utilizados es la
proporción que se denota con la letra P mayúscula y compara el número
de casos o frecuencia (f) de una categoría dada con el tamaño total de la
población (N) o con la muestra (n).
POBLACIÓN TAMAÑO N
PARÁMETRO
f
P = ------
MUESTRA TAMAÑO n
ESTADÍSTICO
f
P = -------
61
N
n
P es la proporción, f es la frecuencia y N ó n es el tamaño de la
población o muestra respectivamente.
Para entender lo que es un parámetro y un estadístico veamos los
siguientes ejemplos:
PARÁMETRO: POBLACIÓN tamaño N
f
P = -------N
1) Supongamos que en tu biblioteca personal tienes
distribuidos de la siguiente manera :
CATEGORÍAS
ASIGNATURA
MATEMÁTICAS
ESTADÍSTICA
INGLÉS
HISTORIA
NOVELA
GEOGRAFÍA
No. DE LIBROS
5
4
8
7
15
1
40
40 libros
FRECUENCIAS
(f)
Aquí el tamaño de la población o N es igual a 40, las categorías
formadas por las diferentes asignaturas son 6 y cada una tiene el número
de libros que le corresponde, el cual recibe el nombre de frecuencia y se
denota con la letra efe minúscula (f).
Si consideramos el número de novelas con respecto al tamaño de la
población, formamos la proporción:
15
P = --------- que resulta ser P = 0.375
40
El valor del parámetro tiene mayor sentido cuando lo transformamos en
porcentaje, esto quiere decir que se desea obtener la frecuencia de
ocurrencia de una categoría por cada 100 casos. Para hacer el cálculo de
un porcentaje sólo se multiplica cualquier proporción ya sea de una
población de una muestra por 100, por lo que % = (100) f ó % =(100) f
N
n
62
Estadística Descriptiva
En este caso al valor de P=0.375 lo multiplicamos por 100:
% = (100)(0.375) = (0.375)(100) = 37.5 %
Concluimos entonces que el porcentaje de novelas que tienes en tu
biblioteca es del 37.5 % con respecto al total de libros considerados.
Encuentra el porcentaje de cada una de las categorías con respecto a
N y escríbelas:
ASIGNATURA
PROPORCIÓN
EN PORCENTAJE
(PARÁMETRO)
MATEMÁTICAS
ESTADÍSTICA
INGLÉS
HISTORIA
NOVELA
GEOGRAFÍA
37.5 %
Después de calcular los porcentajes suma todas las proporciones
obtenidas, si tus valores están correctos el resultado debe ser 100% o un
valor aproximado.
ESTADÍSTICO: MUESTRA tamaño n
f
P = -------n
La proporción es un estadístico si se considera el tamaño de una
muestra (n).
2) En una escuela laboran 500 personas, al extraerse una muestra de
90 trabajadores en diferentes áreas se tiene la siguiente tabla:
ÁREA
ADMINISTRATIVA
BIBLIOTECA
DOCENTES
f
20
40
30
90
La proporción del área administrativa con respecto a 90 es:
20
P = -------- = 0.22
90
63
Al tomar el estadístico que se obtuvo y multiplicarlo por 100 se obtiene
el siguiente porcentaje: % = 0.22 (100) = 22 %
El resultado anterior
indica que el 22% de los trabajadores
considerados en la muestra laboran en el área administrativa.
Calcula los valores de los estadísticos y anótalos:
ÁREA
ADMINISTRATIVA
BIBLIOTECA
DOCENTES
ESTADÍSTICO
22%
La suma de esta columna debe ser 100% o un valor aproximado.
3) En una biblioteca se tienen 2,000 volúmenes y se revisa una
muestra tomada al azar formada por 130 libros.
a) La población es finita ya que está formada por el total de volúmenes
de la biblioteca que son 2,000.
b) Muestra integrada por los 130 libros revisados.
c) Parámetro de la población: Comparación entre los libros revisados y
el total de volúmenes que en este caso es 130/2000 = 0.065, este valor
también se puede expresar como porcentaje al multiplicarlo por 100,
entonces se tiene que de un total de 2,000 libros se revisó el 6.5%.
Anteriormente se ha expresado que las características de una
población son los parámetros y las de una muestra estadígrafos o
estadísticos, en cada caso se utilizan símbolos que las representen, como
ejemplo tenemos:
CARACTERÍSTIC
A
MEDIA
VARIANZA
DESVIACIÓN
ESTÁNDAR
64
PARÁMETR
O
µ
σ
σ2
ESTADÍGRAFO
X
s o S
s2 o S2
Estadística Descriptiva
¿QUÉ HE APRENDIDO?
Si al contestar lo que se te pide a continuación tienes dudas, regresa y
vuelve a empezar con más ánimo. Adelante.
1)Escribe un enunciado en donde se identifique claramente la
población y una muestra de la misma.
________________________________________________________
____________________________________________________________
_______________
2)Redacta dos ejemplos en donde no es posible trabajar con la
población, pero si con una muestra representativa de cada una de ellas.
________________________________________________________
____________________________________________________________
_______________
3) Anota dos características básicas de la población finita.
________________________________________________________
____________________________________________________________
_______________
4) Escribe 2 características importantes de la población infinita.
________________________________________________________
____________________________________________________________
_______________
5)Da un ejemplo de parámetro y otro de estadístico como en el inciso
3.
________________________________________________________
____________________________________________________________
_______________
6) Escribe en cada caso si es población finita o infinita:
POBLACIÓN
a)
Número
FINITA/INFINITA
de
alumnos
de
la
ENBA,
65
considerando a los que pertenecen al Sistema
Escolarizado y los del Sistema Abierto y a Distancia.
b) Lanzamiento indefinido de 2 dados, anotando
la suma de puntos.
c) Número de niños del mundo.
d) Libros de la biblioteca de una escuela.
e) Expedientes que se encuentran en trámite en
un Archivo.
f) Documentos que describen la historia del ser
humano en el pasado y en el futuro (considerando
que el mundo nunca será destruido).
7) Arroja 30 veces una moneda, anota el número de cara o cruces y
contesta:
Número de caras ____________________
Número de cruces ____________________
8) Contesta las siguientes cuestiones, considerando el enunciado del
inciso anterior:
a) La población está formada por: ________________________
b) La muestra es: _____________________________________
c) Es finita o infinita la población:_________________________
d) Describe un parámetro.
________________________________________________________
_______
e) Describe un estadístico.
________________________________________________________
_______
66
Estadística Descriptiva
1.3 VARIABLES
Variable es cualquier unidad, cualidad, operación o fenómeno que se
desee analizar.
VARIABLE: FORMA Y TAMAÑO DE LAS SIGUIENTES FIGURAS
a)
b)
Escribe las características diferentes de las figuras para cada una de
las variables:
Variable
Característica de a)
Forma de la figura 1.-.
Tamaño
de
la 2.figura
Característica de b)
1.2.-
Una vez definida la población de interés, el procedimiento para la
obtención de datos indispensables para el uso de métodos estadísticos se
puede dar en dos formas:
1) Recabar información de registros como puede ser el número de
personas que acuden diariamente a una biblioteca o a un archivo.
2) Llevar a cabo una encuesta (cuestionario formado por una serie de
preguntas relacionadas lógicamente con un tema central).
En ambos casos se obtendrán características de interés sobre la
población con la que se está trabajando, éstas reciben el nombre de
Variables.
VARIABLE (de respuesta). Característica de interés acerca de cada
elemento de una población o una muestra representativa que permite
ordenar las observaciones e identificar sus diferencias. Son variables la
edad de un estudiante, el color de su pelo, la asignatura a la cual pertenece
67
un libro o clasificación de expedientes según el tipo de archivo al que
pertenecen.
Se tienen 2 tipos de variables: CUALITATIVA Y CUANTITATIVA
CUALITATIVA se refiere a cualidad. Los datos cualitativos se
consideran en categorías o grupos.
CUANTITATIVA se refiere a cantidad. Los datos cuantitativos están
representados por un número.
TIPOS DE VARIABLES:
NOMINAL
Variables que no se pueden ordenar
CUALITATIVA
Describe y clasifica
en categorías a los
elementos de una
muestra o población
ORDINAL
Variables que se pueden ordenar
VARIABLE
CUANTITATIVA
Permite el conteo
o medición
DISCRETA
Variables que sólo toman valores enteros
CONTINUA
Variables con valores enteros y/o decimales
VARIABLE CUALITATIVA O ATRIBUTO. Es el resultado de un
proceso que permite describir o formar categorías con los elementos de
una población y se divide en Nominal y Ordinal.
VARIABLE CUALITATIVA NOMINAL. Cuando los valores de una
variable cualitativa permiten únicamente ubicar a cada individuo en una
categoría y no hay orden entre los valores, por ejemplo si a los
alumnos del grupo de Estadística Descriptiva se les pregunta el
nombre de la escuela en donde estudiaron bachillerato, algunas de las
posibles respuestas serían: Preparatoria, CCH, Bachilleres.
VARIABLE CUALITATIVA ORDINAL. Cuando a los valores de
una variable se les puede dar un orden, por ejemplo para conocer el
gusto de los alumnos de la ENBA por las Matemáticas, se podrían
considerar las respuestas: Mucho, Regular o Poco, las cuales se
pueden ordenar de mayor a menor o viceversa.
68
Estadística Descriptiva
VARIABLE CUANTITATIVA O NUMÉRICA. Es el resultado de un
proceso que cuantifica, es decir, que cuenta o mide (longitud o peso), a
estas variables se les asignan números reales con los cuales tiene sentido
efectuar operaciones aritméticas, así es posible compararlas, como
ejemplo tenemos el número de libros de una materia determinada o
número de expedientes que tiene un Archivo de Concentración. Este tipo de
variable se divide en Discreta y Continua.
VARIABLE CUANTITATIVA DISCRETA. Toma valores enteros,
un ejemplo es la cantidad de alumnos que asisten a una conferencia.
VARIABLE CUANTITATIVA CONTINUA. Toma valores enteros y
decimales, como el peso de cada uno de los trabajadores que laboran
en un Archivo.
DATO. Valor de la variable asociado a un elemento de la población o
muestra. Si la muestra representativa es el grupo de Estadística Descriptiva
y la variable es la edad (cuantitativa discreta si se toman sólo los años
cumplidos), se dice que el dato de “x” estudiante es 23 años.
¿QUÉ HE APRENDIDO?
Es necesario que respondas lo que se te pide enseguida, si tienes
dudas vuelve a iniciar la lectura de este tema.
1) Completa el siguiente cuadro y agrega en cada caso un ejemplo de
la variable de que se trata:
CUALITATIVA
VARIABLE
CUANTITATIVA
69
2) Identifica en cada caso si se trata de una variable nominal, ordinal,
discreta o continua:
TIPO DE VARIABLE
a) Nombre
________________________
b) Color de cabello
________________________
c) Peso
________________________
d) Color de ojos
________________________
e) Estado civil
________________________
f) Sexo
________________________
g) Profesión
________________________
h) Número de alumnos de la ENBA
________________________
i) Número
de
preguntas
________________________
70
en
un
examen
Estadística Descriptiva
j) Resultado de una encuesta
________________________
k) Número
de
páginas
de
un
expediente
________________________
l) Libros
de
una
biblioteca
________________________
m)Satisfacción al realizar una investigación
en una biblioteca o archivo
________________________
71
1.4 ESCALAS DE MEDICIÓN
ESCALA DE 1 EN 1
0
1
2
3
ESCALA DE 2 EN 2
0
2
4
6
Escala: Sucesión ordenada de puntos en la que se considera a cada
una de las partes del mismo tamaño.
Medida: Número o denominación que se
observación. Si se obtiene un número que
capacidades, se llama medición cuantitativa, y
denominación que sólo registra características,
conoce con el nombre de medición cualitativa.
asigna a la unidad de
expresa dimensiones o
si el resultado es una
atributos o actitudes, se
Las variables son conceptos fundamentales para el estudio de los
métodos estadísticos, su clasificación muestra el nivel de medición de las
características que pueden ser cuantitativas o cualitativas.
Las mediciones cuantitativas son de dimensión o capacidad como:
Estatura, peso, volumen, área, tiempo, longitud, etc.
Las mediciones cualitativas se refieren a características, atributos o
actitudes, las cuales no pueden ser representadas numéricamente tal es el
caso de: Opiniones, formación de grupos por ingreso familiar, profesión,
religión, clasificación de libros o expedientes por el estado físico que
presentan.
En una investigación, cuando se comparan los valores (o datos)
obtenidos, se está realizando un proceso de medición el cual permite
establecer una escala de valores. De acuerdo al tipo de variables se tienen
las siguientes escalas:
1.4.1 ESCALA NOMINAL. Cuando a las categorías utilizadas sólo
se les dan nombres arbitrarios a manera de etiquetas, sin que exista
72
Estadística Descriptiva
orden o relación entre ellas, como puede ser agradable o no agradable.
En esta escala los datos que son iguales forman una categoría y al
contarlos se obtiene la frecuencia absoluta o simplemente frecuencia.
En esta escala se proporciona información sobre la forma en que
están organizadas las categorías, aunque no indica la magnitud de las
diferencias entre los números, como en el caso de que en una biblioteca
se desee saber con qué material se cuenta en el área de consulta:
Libros, Revistas, Enciclopedias o Folletos. En un archivo podemos
investigar el sexo de los investigadores a fin de averiguar si entre ellos
hay más hombres que mujeres, de esta forma tendríamos las opciones
masculino o femenino.
1.4.2 ESCALA ORDINAL. Las categorías que se construyen pueden
ser ordenadas o jerarquizadas, según el nivel en que se sitúa una
determinada categoría con relación a otra, sin utilizar valores
cuantitativos, aunque las variables si se pueden relacionar por medio de
los operadores relacionales como son mayor (>), menor(<) o igual(=) o
comparar, como ejemplo de esta escala tenemos los resultados de una
encuesta en donde se desea conocer la satisfacción de un usuario,
formándose las categorías: Ninguna (N), Regular (R), Buena (B) y
Excelente (E). Un archivo puede ser mayor o menor que cualquier otro si
tomamos como medida de comparación una variable determinada.
1.4.3 ESCALA DE INTERVALO. Usa como 0 un valor arbitrario y se
utiliza cuando al formar categorías se está en posibilidad no sólo de
clasificar y ordenar, sino además de cuantificar las diferencias entre
ellas. En este caso se requiere de establecimiento de algún tipo de
medida, que puede considerarse como patrón o norma y la aplicación de
este patrón se puede llevar a cabo tantas veces como sea necesario,
originando los mismos resultados, los patrones utilizados pueden ser
metros, kilos, litros, pesos, etc. Esta escala indica que un individuo u
objeto es tantas unidades más grande o más pequeño, más pesado o
más ligero, más claro o más obscuro que otro, etc. Un ejemplo de esta
escala es la puntuación obtenida por una persona en un test de
inteligencia, en donde el cero no significa que un individuo tenga vacía la
cabeza.
1.4.4 ESCALA ABSOLUTA o racional. Las distancias entre puntos
en la escala son precisos y conocidos y no existe cero absoluto. En esta
escala las unidades son fijas y normalizadas, permitiéndonos realizar
análisis mucho más rigurosos y precisos. Ejemplo: Si la biblioteca “x”
tiene un presupuesto para materiales de $4,600, un sistema semejante
73
$800 y otro $650, se puede expresar exactamente y sin dificultad las
diferencias en pesos y en porcentajes y definir cómo es un presupuesto
con respecto al otro, observemos que en esta escala no se puede
cambiar nada, ya que básicamente se utiliza para conteos.
¿QUÉ HE APRENDIDO?
Ha llegado el momento de hacer una revisión del aprendizaje
adquirido.
1) Escribe tu propia definición de escala.
________________________________________________________
____________________________________________________________
_______________
2) Elabora un cuadro que muestre los diferentes tipos de escalas con
un ejemplo cada una:
ESCALAS
3) Indica en cada caso el tipo de medición que se está utilizando
(Escalas: Nominal, Ordinal, de Intervalo o Absoluta):
a) Se inscriben varios alumnos de la ENBA para participar en un
concurso y a cada uno se le entrega un número para su participación.
________________________
b) Al terminar el concurso se informa el resultado y aparece un
primer lugar, segundo, etc. Los resultados forman una ESCALA
________________________
c) Si además a cada participante se le tomó el tiempo de exposición
de su proyecto bajo las mismas bases, se puede saber quién es el más
74
Estadística Descriptiva
rápido y quién el más lento. A estos resultados se les puede incluir en
una ESCALA ________________________
d) Cómo es la medición que se hace al anotar si una persona recibe
el primer premio, el segundo, etc. ________________________
e) Un Archivista anota el número que le corresponde a cada legajo
en una muestra específica .________________________
f) Un Bibliotecario registra el número de usuarios que solicitan
determinado
material
para
sus
investigaciones
.
________________________
g) Uso del Sistema Dewey. ________________________
h) Público que se presenta en una biblioteca o en un archivo para
solicitar información. ________________________
i) Comparación del tipo y cantidad de libros que se encuentran en
una biblioteca. ________________________
75
Elabora el Resumen de la Unidad I completando el siguiente mapa
conceptual, al final de la guía lo encontrarás resuelto, de ser posible,
confronta tus respuestas y corrígelas en caso de ser erróneas:
ESTADÍSTICA
Ciencia de la recopilación,
clasificación, presentación
e interpretación de datos
OBJETO
Inferir el comportamiento
de una población a
través del análisis de
t
SE CLASIFICA EN
TIENEN COMO BASE
UNA
MUESTRA REPRESENTATIVA:
O UNA PARTE
POBLACIÓN QUE ES:
PUEDE SER:
1) FINITA
2) INFINITA
SUS CARACTERÍSTICAS
SE DENOMINAN
VARIABLES Y SON:
CUALITATIVA
CUANTITATIVA
CLASIFICÁNDOSE SEGÚN LAS SIGUIENTES
ESCALAS DE MEDICIÓN:*
*Escalas de medición:
a) Nominal.- Se utiliza como medida de identificación con variables
nominales.
b) Ordinal.- Permite la manipulación de variables ordinales.
c) Intervalo o Absoluta:- Maneja variables cuantitativas.
76
Estadística Descriptiva
EVALUACIÓN
Lee cuidadosamente cada inciso y contesta en forma clara y breve lo
que se te solicita, ya que esta evaluación se la debes enviar a tu asesor:
1) Escribe tu propia definición de Estadística
________________________________________________________
____________________________________________________________
____________________________________________________________
_______________________
2) Se sabe que cierto Archivo tiene un total de 5,000 expedientes, si a
cada uno de ellos se le asigna un número para su identificación, contestar:
a) Cuando se habla de 5,000 expedientes en total nos estamos
refiriendo a la ________________
b) La escala que se ha utilizado es ______________ ya que
____________________________________________________________
________
3) En la biblioteca de una Institución Educativa se pretende dar pláticas
durante el período intersemestral, al personal docente y administrativo
sobre el uso y manejo de sus diferentes servicios, para ello realiza una
encuesta con 850 personas para saber su opinión, si 245 están a favor
contestar lo siguiente:
a) La población está formada por:
________________________
b) ¿Es población finita o infinita?
________________________
c) ¿Cuál es la muestra?
________________________
d) Describir un parámetro
________________________________________________________
____________________________________________________________
______________
e) Calcular un estadístico
77
________________________________________________________
____________________________________________________________
_______________
f) ¿Cuál consideras que es la variable de interés?
________________________________________________________
____________________________________________________________
_______________
g) ¿A qué escala pertenece esta variable? Explica tu respuesta
________________________________________________________
____________________________________________________________
_______________
INSTRUCCIÓN GENERAL
De los siguientes dos ejercicios, resuelve el que corresponda a tu área,
en caso de que así lo desees, puedes resolver ambos.
4) Acude a una biblioteca de tu localidad y pregunta:
- Total de libros de la biblioteca
- Número de volúmenes que se tiene para préstamo a domicilio
- Volúmenes para préstamo en sala
- ¿Del total de volúmenes para préstamo a domicilio cuál es el área del
conocimiento que tiene mayor número de libros?
- ¿En qué lugar se registra mayor movimiento, en préstamo a domicilio
o en consulta en sala?
Con la información que obtengas contesta lo siguiente:
a) ¿Cuál es la población?
________________________________________________________
_______
b) ¿Se trata de una población finita o infinita?
________________________________________________________
_______
c) Anota como mínimo 3 diferentes muestras que puedes formar
considerando el total de libros:
78
Estadística Descriptiva
________________________________________________________
_______
d) Efectúa los cálculos necesarios para encontrar la proporción que
existe entre los libros que se prestan y el total de libros, anota el resultado y
expresa si se trata de un parámetro o de un estadístico.
________________________________________________________
_______
d) Calcula la proporción de ejemplares de la asignatura que más se
presta con respecto a los libros que se prestan a domicilio e indica si se
trata de un parámetro o de un estadístico.
________________________________________________________
_______
5) Investiga en un Archivo de Trámite (Oficina de Gobierno
Administrativa, Archivo Estatal, Municipal o de la Localidad):
-Total de expedientes que maneja el Archivo
-Promedio de documentos que entran diariamente
-Promedio de documentos que salen diariamente
-Qué día de la semana se recibe más correspondencia y qué día menos y
preguntar el promedio en cada caso
-Número de expedientes que son susceptibles de ser prestados para su
consulta
Con la información que obtengas contesta lo siguiente:
a) ¿Cuál es la población?
________________________________________________________
_______
b) ¿Se trata de una población finita o infinita?
________________________________________________________
_______
c) Anota como mínimo 3 diferentes muestras que puedes formar en el
Archivo al que acudiste:
________________________________________________________
_______
d) Calcular la proporción entre el número de expedientes susceptibles
de ser prestados para su consulta y el total de expedientes con que cuenta
el archivo, indica si se trata de un parámetro o de un estadístico:
79
________________________________________________________
_______
e) Calcula un estadístico de la información obtenida:
________________________________________________________
_______
ENVÍA A TU ASESOR
Felicidades, has logrado un importante avance.
80
Estadística Descriptiva
UNIDAD 2
PRESENTACIÓN DE DATOS
Una vez que se tiene una muestra aleatoria de tamaño n de la
población de interés, los datos considerados deben ser ordenados y
presentados en tablas de distribución que pueden ser simples, cuando se
habla de datos cualitativos o de una población o muestra pequeña, o
para datos agrupados cuando se tiene una población o muestra grande.
Los datos presentados en una tabla permiten observar claramente la
naturaleza y comportamiento de la información sobre la cual se tiene
interés.
¿QUÉ VOY A APRENDER EN ESTA UNIDAD?
A organizar, manejar y presentar los datos obtenidos a través de una
investigación en una Tabla de Distribución de frecuencia simple o para
datos agrupados que te faciliten identificar el comportamiento de una
variable.
Antes de iniciar esta unidad realiza las siguientes actividades
diagnósticas.
81
DIAGNÓSTICO
1) Escribe los primeros conceptos de Estadística que te quedan
claros.
________________________________________________________
____________________________________________________________
_______________
2) Si al ir a comprar un libro te informan que su costo es de $120.00
pero que tiene un descuento del 15%, ¿cuánto vas a pagar?
__________________.
Describe el procedimiento que realizaste para su cálculo.
________________________________________________________
_______
3) Ahora, supongamos que otro libro cuesta $150.00 más el 15% de
IVA ¿cuánto pagarías por él? ___________________.
4) Ordena en forma ascendente y descendente los siguientes números
8, 7, 1, 4, 10, 2
ASCENDENTE:____________________________________________
______
DESCENDENTE:__________________________________________
_______
Es muy importante que no olvides lo que vas aprendiendo en cada
unidad, por ello en la pregunta 1 del diagnóstico se te solicita que anotes los
conceptos estadísticos que consideras más importantes, si no los recuerdas
repasa tu resumen y contesta en forma correcta. No olvides que la
constancia en el estudio da sus frutos al alcanzar una meta.
82
Estadística Descriptiva
En las preguntas 2 y 3 tuviste que haber realizado cálculos para
encontrar los porcentajes que se te solicitan, si tus respuestas son $102.00
y $172.50 respectivamente puedes continuar, si no fue así lee con atención
lo siguiente:
Recordemos que el porcentaje de un número es igual al mismo
número dividido entre 100, esto es:
5
5% =------ = .05
100
9
9% =------ = .09
100
10
10% = ---- = .10
100
y en general si a es cualquier número
a
a% =-------100
Si utilizamos esta sencilla regla para el cálculo del 15% de $120.00
entonces tenemos que multiplicar 120 por .15 y obtenemos 18 que se resta
a 120 porque se trata de un descuento, el resultado es $102.00 a pagar por
el libro.
De igual forma se calcula el 15% de $150.00 que es 22.5 el cual se
suma al costo dando un total de $172.50, ya que se trata de un cargo al
costo.
Finalmente, en la ordenación de números te habrás dado cuenta que
cuando se te solicita orden ascendente escribes el número menor y
continúas escribiendo los restantes hasta llegar al número más grande y la
numeración en forma descendente se obtiene iniciando con el mayor y
terminando con el menor.
Bien, ¿ya estás listo para continuar? Adelante.
83
2.1 TIPOS DE DATOS
En el desarrollo de este tema, consideramos 3 tipos de datos:
Categóricos, Ordenados por rango y Métricos. Con el propósito de entender
su utilidad, para cada uno de ellos elaboraremos una tabla o cuadro
estadístico colocando en la primera columna las diferentes categorías que
se forman al tomar en cuenta al total de datos, sin que se repita ninguna y,
en otra columna el número de elementos que pertenecen a cada categoría.
TABLA O CUADRO ESTADÍSTICO
CATEGORÍAS
frecuencias absolutas o frecuencias (f)
A
número de datos que caen en esta
categoría
B
“
“
TOTALES
suma de todas las frecuencias
2.1.1 DATOS CATEGÓRICOS. Agrupan a los individuos en categorías,
contando el número de sujetos que pertenecen a cada una. El número que
indica cuántos elementos tiene una categoría recibe el nombre de
frecuencia absoluta o simplemente frecuencia y se denota con la letra efe
minúscula “f”. Al realizar el conteo cada sujeto debe adaptarse exactamente
a una categoría.
Supongamos que en cierta área existen 33 bibliotecas, las cuales se
pueden agrupar por categorías obteniéndose la tabla siguiente:
BIBLIOTECAS DEL ÁREA “Y”
TIPO DE BIBLIOTECAS
NÚMERO
(f)
ACADÉMICAS
2
Categorías PUBLICAS
8
categoría
ESCOLARES
20
ESPECIALIZADAS
3
Total:
frecuencia de cada
33
En este cuadro aparece la variable nominal tipo de bibliotecas con las
categorías: Académicas, Públicas, Escolares y Especializadas; en la
segunda columna están sus frecuencias respectivas.
84
Estadística Descriptiva
Si se trata de Archivos, también se puede elaborar un cuadro con
datos categóricos. Tomemos como ejemplo una Secretaría de Estado.
SECRETARÍA DE ESTADO “X”
TIPO DE ARCHIVO
NÚM. DE EXPEDIENTES
TRÁMITE
25
CONCENTRACIÓN
4
HISTÓRICO
1
Total:
30
2.1.2 DATOS ORDENADOS POR RANGO. Establecen un orden entre
categorías y son utilizados para comparar.
Considerando la tabla que muestra las diferentes bibliotecas en una
área, es fácil comparar la categoría de Bibliotecas Académicas con la de
Bibliotecas Escolares, de acuerdo a las frecuencias de cada una de ellas se
puede asegurar que es mayor el número de Escolares que de Académicas.
BIBLIOTECAS DEL ÁREA “Y”
TIPO DE BIBLIOTECAS
NUMERO
ACADÉMICAS
2
PUBLICAS
8
ESCOLARES
20
ESPECIALIZADAS
3
Total:
33
Otro ejemplo en donde se puede utilizar la ordenación por rango es en
la edición de libros en donde las categorías son las fechas de edición:
BIBLIOTECA “X”
FECHA DE EDICIÓN
ENERO
1991
JUNIO
1991
FEBRERO
1992
AGOSTO
1992
Total:
NÚMERO
23
10
21
3
57
2.1.3 DATOS MÉTRICOS. Permiten la introducción de medidas, lo cual
facilita la comparación de los datos obtenidos.
85
Si consideramos nuevamente la edición de libros y asignamos
unidades (años) con intervalos iguales, se pueden efectuar operaciones
aritméticas:
BIBLIOTECA “X”
AÑO DE EDICIÓN
1991
1992
Total:
NÚMERO
33
24
57
Con esta información se puede establecer la comparación entre los
dos años de edición que aparecen en la tabla.
Es posible efectuar esta misma comparación si se consideran los
documentos de un archivo con respecto al año de su elaboración.
¿QUÉ HE APRENDIDO?
1) Haz un cuadro que muestre los diferentes tipos de datos anotando
además, un ejemplo de cada uno.
TIPOS DE DATOS
2) Al investigar en una biblioteca escolar el sexo de usuarios que
solicitan préstamo a domicilio, a fin de conocer los elementos que forman
cada categoría se encontró:
BIBLIOTECA “X”
PRÉSTAMO A DOMICILIO
86
NÚMERO
Estadística Descriptiva
HOMBRES
MUJERES
Total:
210
198
408
En cada uno de los incisos escribe el tipo de dato que se está
utilizando y que pueden ser categóricos, ordenado por rango o métrico.
a)
Los
datos
___________________
son
de
tipo
__________________porque
b) Al comparar el número de hombres y mujeres se están manejando
los datos tipo ________________.
c) Si se considerara el servicio de préstamo a domicilio mensual se
estaría trabajando con datos ________________.
87
2.2 DISTRIBUCIÓN DE FRECUENCIAS
6
4
1
1, 2, 3, 4, 5, 6
3
2
5
Datos sin organizar
Datos organizados
Una vez que se ha recopilado información ya sea por medio de una
encuesta o a través de una investigación, sobre una población y decidido
trabajar con ella si es pequeña o con una muestra representativa si es muy
grande, se obtiene un arreglo de datos en desorden que no es de gran
utilidad para conocer el comportamiento de la información, lo cual provoca
la necesidad de elaborar tablas de distribución de frecuencias.
Iniciaremos la explicación de dichas tablas con un ejemplo muy
sencillo: El Departamento de Control Escolar informa que el número de
alumnos de la Escuela Nacional de Biblioteconomía durante el semestre 97I es de 621 de los cuales 270 pertenecen a Archivonomía y el resto a
Biblioteconomía.
Con este enunciado es muy difícil analizar y comparar los elementos
que pertenecen a cada categoría, sin embargo, si elaboramos una tabla de
distribución de frecuencia simple veremos que es fácil identificar las
categorías y sus frecuencias respectivas:
TABLA DE DISTRIBUCIÓN DE FRECUENCIA SIMPLE
Título
Período
Encabezados
cuerpo
Final
ALUMNOS DE LA ENBA
Semestre 97-I
CARRERA
NÚM.DE ALUMNOS
(X)
(f)
ARCHIVONOMÍA
270
BIBLIOTECONOMÍA
351
Total:
621
Fuente: Información proporcionada por la Subdirección de Planeación y Evaluación de la
ENBA a través de su Departamento de Control Escolar el 28 de abril de 1997.
Pie: Sólo se ha considerado el total de alumnos en el Sistema Escolarizado.
88
Estadística Descriptiva
Las tablas de distribución de frecuencias o tabla de frecuencias
permiten estructurar y ordenar la información, para que su contenido sea lo
más claro posible siempre se debe incluir:
•
•
•
•
•
•
•
Título. Describe la información más importante del problema.
Fecha o Período de tiempo en que se realizó la investigación.
Encabezado. Informa el contenido de cada columna.
Cuerpo. Agrupa la información en categorías con sus frecuencias
respectivas.
Final. Registra los totales de las columnas numéricas.
Fuente. Se debe especificar cómo, cuándo, quién y dónde se
tomaron los datos.
Pie. Contiene observaciones. (En algunos casos no existe).
Una vez que ya identificamos las partes que forman una tabla de
distribución de frecuencias, conozcamos los diferentes tipos de
distribuciones de acuerdo a la variable que se está manejando.
2.2.1 SIMPLES
DISTRIBUCIÓN
NOMINALES
DE
FRECUENCIAS
SIMPLES
PARA
DATOS
Esta tabla de distribución es útil cuando se trata de una variable de tipo
nominal.
1) Al
grupo 6101 formado por 21 alumnos de la carrera de
Archivonomía en la ENBA se le preguntó cuál es la materia de su
preferencia de Estadística Descriptiva (ED), Inglés (I) o Computación (C),
siendo las respuestas: ED, I, ED, I, C,C,C, I, ED, I, C,C,C, I, C,C,C,C,C, I, C.
Con esta información elaboraremos un tabla de distribución de
frecuencias simple que muestre los datos de la variable nominal Materia de
preferencia.
89
MATERIAS DE PREFERENCIA DE LOS ALUMNOS DE ARCHIVONOMÍA DE LA ENBA
GRUPO 6101
-SEMESTRE 97-1
ASIGNATURA
NÚMERO DE ALUMNOS
ESTADÍSTICA
3
DESCRIPTIVA
INGLÉS
6
COMPUTACIÓN
12
TOTAL:
21
Fuente: Encuesta realizada por la Coordinación de la Carrera de
Archivonomía
al grupo 6101 en junio de 1997.
Observaciones: Sólo se consideró al turno matutino y a los
Alumnos inscritos en el Sistema Escolarizado.
Las tablas de distribución permiten manejar la información más
fácilmente, con los datos del cuadro anterior calcularemos algo tan
importante como lo es la proporción en porcentaje de cada categoría con
respecto a la muestra:
a) El porcentaje de alumnos que prefieren Estadística Descriptiva es:
f
3
% = -------- (100) = ------- (100) = 14.28%
n
21
b) El porcentaje de alumnos que prefieren Inglés es:
f
6
% = -------- (100) = ------- (100) = 28.57%
n
21
c) El número de alumnos que prefiere Computación representa un
porcentaje de:
f
12
% = -------- (100) = ------- (100) = 57.14%
n
21
Estos cálculos se pueden agregar en la tabla de distribución teniendo
como encabezado frecuencia relativa o fr:
90
Estadística Descriptiva
MATERIAS DE PREFERENCIA DE LOS ALUMNOS DE ARCHIVONOMÍA DE LA ENBA
GRUPO 6101
SEMESTRE 97-1
ASIGNATURA
NÚMERO DE ALUMNOS
fr (%)
ESTADÍSTICA
3
14.28
DESCRIPTIVA
INGLÉS
6
28.57
COMPUTACIÓN
12
57.14
TOTAL:
21
99.99
Fuente: Encuesta realizada por la Coordinación de la Carrera de
Archivonomía
al grupo 6101 en junio de 1997.
Observaciones: Sólo se consideró al turno matutino y a los
alumnos inscritos en el Sistema Escolarizado.
La tabla de distribución de frecuencias simple no sería de gran utilidad
si sólo se llegara hasta aquí, su importancia radica en que permite analizar
la información que contiene, como por ejemplo comparar las frecuencias
entre las categorías, lo que recibe el nombre de razón que es un cociente
en donde se comparan dos cantidades que se encuentran en las mismas
unidades.
LECTURA 1
Con el propósito de que conozcas un poco más sobre la proporción
además de saber cómo y para qué se calculan la razón y las tasas, te
sugiero leas la primera lectura que se encuentra al final de esta guía, escrita
por Ray I. Carpenter y que forma parte del libro “Métodos Estadísticos para
Bibliotecarios”. (páginas de la 25 a la 30).
Se hace hincapié en que estos conceptos también son de vital
importancia para los Archivónomos, como lo veremos más adelante con
ejemplos.
Para la mejor comprensión de la lectura subraya los conceptos más
importantes, realiza anotaciones al margen, busca las palabras
desconocidas en el diccionario y elabora un resumen que te permita
confrontar el desarrollo del tema.
Después de leer regresa para continuar con más ánimo.
91
Una vez realizada tu lectura reforzaremos con ejemplos su
aprendizaje. Consideremos los datos de la tabla construida antes de la
lectura.
ASIGNATURA
ESTADÍSTICA
DESCRIPTIVA
INGLÉS
COMPUTACIÓN
TOTAL:
NÚMERO DE ALUMNOS
3
fr (%)
14.28
6
12
21
28.57
57.14
99.99
Si el número de alumnos que prefiere Estadística Descriptiva es 3 y los
que prefieren Inglés son 6, ¿cuál es la razón entre los alumnos que tienen
estas preferencias?:
frecuencia de Estadística Descriptiva
Razón = ---------------------------------------------frecuencia de Inglés
3
1
Razón = -------- = -----6
2
Conclusión: Por cada alumno que prefiere Estadística Descriptiva
existen 2 que prefieren Inglés, esto es, la preferencia es 1 a 2.
Veamos la razón que existe entre los alumnos que prefieren
Computación con los que prefieren Estadística Descriptiva:
frecuencia de Computación
Razón = ---------------------------------------------frecuencia de Estadística Descriptiva
Razón = ----------- = -------Conclusión:
________________________________________________________
____________________________________________________________
_______________
92
Estadística Descriptiva
2) Observa la información que aparece en la siguiente tabla:
ALUMNOS INSCRITOS EN BIBLIOTECONOMÍA POR SEXO
Semestre 97-I
SEXO
NÚM.DE ALUMNOS
(X)
(f)
HOMBRES
288
MUJERES
144
Total:
432
f1 es la frecuencia de una categoría y f2 de otra diferente.
f1
Razón = ------f2
Si consideramos a f1 como la frecuencia de la categoría de hombres
entonces f1=288 y similarmente si tomamos a f2 como la frecuencia de la
categoría de mujeres f2=144.
Al comparar el número de hombres con el número de mujeres que
estudian la carrera de Biblioteconomía:
288
Razón = --------144
Como 288 es el doble de 144 entonces:
288
2
Razón= ------------- = ---144
1
Conclusión: La razón indica que por cada 2 hombres hay 1 mujer o
viceversa que por cada mujer hay 2 hombres.
3) Con la información que se te muestra contesta lo que se te pide:
SECRETARÍA DE ESTADO “X”
TIPO DE ARCHIVO
NÚM. DE EXPEDIENTES
TRÁMITE
25
CONCENTRACIÓN
4
HISTÓRICO
50
Total:
79
a) Cuál es la razón entre los expedientes en trámite y los que se
encuentran en el Archivo Histórico:
Razón = ---------
93
Conclusión:_______________________________________________
____________________________________________________________
_______________
b) Calcula la proporción de expedientes en trámite con respecto al
total.
________________________________________________________
____________________________________________________________
_______________
c) Escribe la proporción anterior en forma de porcentaje.
________________________________________________________
____________________________________________________________
_______________
Ahora que ya hemos entendido el concepto de razón continuaremos
con un ejemplo en donde se utiliza la tasa de cambio.
4) Si en la biblioteca de la escuela había 456 libros al inicio de un
período escolar y al finalizar el mismo este número disminuyó a 422 ¿cuál
es la tasa de cambio de libros extraviados?
En la lectura se nos indicó que la forma de calcular la tasa de cambio
es la siguiente:
Valor final - Valor inicial
Numerador
Tasa de cambio = --------------------------------------- = -------------------Valor inicial
Denominador
En el numerador se escribe la diferencia entre el valor inicial del
período y el valor final del mismo:
422 - 456= -34
Nota: Si la cantidad que se obtiene es negativa representa una disminución y si es positiva
se trata de un incremento.
En el denominador se escribe el valor de la variable al principio del
período:
456
-34
Tasa de cambio = --------- = -0.074 = -7.4%
456
94
Estadística Descriptiva
Como el resultado es negativo se obtiene la siguiente conclusión:
Durante el período escolar considerado el acervo ha disminuido en un
7.4%.
5)Si en el año de 1990 en un Archivo existían 256,000 expedientes y en
1996 se incrementó este número a 321,000 ¿cuál es la tasa de cambio en el
período de 6 años?
321,000 - 256,000
65,000
Tasa de cambio = -------------------------- = -------------------=.2539 =25.39%
256,000
256,000
Conclusión: El Archivo incrementó su número de expedientes en
65,000, lo cual da como resultado un crecimiento del 25.39% en un período
de 6 años.
¿QUÉ HE APRENDIDO?
Para poder continuar se requiere que contestes correctamente lo que
se solicita en cada inciso:
1)
De
acuerdo
a
la
lectura
la
razón
es
útil
para__________________________
_______________________________________________________________
_____
2)
La
tasa
de
cambio,
permite______________________________________
_______________________________________________________________
_____
3) En una biblioteca se tienen 2,340 libros para préstamo a domicilio y
780 para consulta interna. Con esta información identifica en cada caso si
se tiene que calcular una razón, proporción o tasa de cambio.
a) A fin de establecer la relación que existe entre los libros para
préstamo a domicilio con los de consulta interna.
___________________________________________________________
____
95
b) Para conocer cuántos libros existen en una categoría con respecto a
la otra.
___________________________________________________________
____
c) Con el objeto de calcular el incremento de libros durante los últimos
dos años.
________________________________________________________
_______
4) Pregunta a 15 personas su grado máximo de estudios y con las
respuestas elabora una tabla de distribución simple.
DISTRIBUCIÓN
ORDINALES
DE
FRECUENCIAS
SIMPLES
DE
DATOS
Las categorías utilizadas deben tener un orden al ir construyendo la
distribución de frecuencias, algunos autores consideran el orden de menor
a mayor (ascendente) y otros por el contrario ordenan los datos de mayor a
menor (descendente). En esta guía se utilizará el orden ascendente.
6) Un ejemplo que se puede presentar es el hecho de conocer la
satisfacción de los usuarios en relación con los servicios que presta al
público ya sea una Biblioteca o un Archivo, en cuyo caso lo más
conveniente es tomar una muestra que represente al total de la población y
realizar una encuesta, supongamos que los resultados de la misma son:
Ninguna = 20, Regular = 30, Buena = 15 y Excelente = 18.
Con estos datos ya se está en posibilidad de elaborar una Tabla de
Distribución de Frecuencias Simple que muestre claramente la información
obtenida, ya sea desde su valor más pequeño hasta el más alto o viceversa
como se ilustra en las dos tablas siguientes:
Orden ascendente
ENCUESTA PARA CONOCER LA SATISFACCIÓN
DEL USO DE SERVICIOS
SATISFACCIÓN
No. DE USUARIOS
NINGUNA
20
REGULAR
30
BUENA
15
EXCELENTE
18
TOTAL
83
96
Estadística Descriptiva
Orden descendente
ENCUESTA PARA CONOCER LA SATISFACCIÓN
DEL USO DE SERVICIOS
SATISFACCIÓN
No. DE USUARIOS
EXCELENTE
18
BUENA
15
REGULAR
30
NINGUNA
20
TOTAL
83
¿QUÉ HE APRENDIDO?
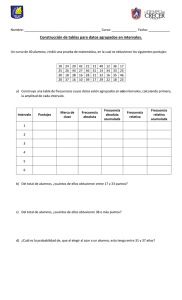
1) Escribe la diferencia que existe entre la tabla de distribución de
frecuencias simples para datos ordinales y la de datos nominales.
________________________________________________________
____________________________________________________________
_______________
2) Elabora una tabla de distribución de frecuencia simple con todos sus
elementos, considerando la información que obtengas al preguntar a 15 de
tus compañeros si les gustan las Matemáticas, utilizando para ello las
categorías: Nada, Poco, Regular y Mucho.
3) Calcula la proporción que existe entre las personas a quienes les
gusta mucho Matemáticas y a las que no les gusta.
________________________________________________________
____________________________________________________________
_______________
DISTRIBUCIÓN DE FRECUENCIA SIMPLE DE DATOS CONTINUOS
O DISCRETOS
97
Cuando se tiene un número pequeño de observaciones representadas
por números continuos o discretos, se construye una tabla parecida a las
dos explicadas anteriormente, escribiendo en la primera columna la variable
y en la segunda la frecuencia con que aparecen los datos.
Como ejemplo usaremos las calificaciones de Cómputo obtenidas por
25 alumnos y que son: 3 alumnos obtuvieron cinco, 5 alumnos seis, 6
alumnos siete, 5 alumnos ocho, 3 alumnos nueve y 3 alumnos diez.
CALIFICACIONES DEL GRUPO 337
PRIMER PARCIAL DE CÓMPUTO
SEMESTRE 97-I
CALIFICACIÓN
No. DE ALUMNOS
(X)
(f)
5
3
6
5
7
6
8
5
9
3
10
3
TOTAL
25
Fuente: Lista del grupo 337 proporcionada por el Profesor de la Materia.
¿QUÉ HE APRENDIDO?
Observa la tabla que se acaba de construir y contesta:
1) En este caso la primera columna contiene ___________ que
representan a la variable cuantitativa.
2) ¿Existe alguna diferencia entre esta tabla y las dos construidas
anteriormente?
Explica
tu
respuesta:______________________________________
____________________________________________________________
________
3) ¿La distancia que recorren tus compañeros en metros de sus
respectivas casas al trabajo podrían proporcionarte información para
98
Estadística Descriptiva
construir una tabla para datos continuos o discretos? Explica tu
respuesta:____________________________
____________________________________________________________
________
4) ¿Qué categorías te gustaría considerar en el inciso 3?
____________________________________________________________
____________________________________________________________
________________
99
2.2.2 PARA DATOS AGRUPADOS
DISTRIBUCIÓN DE FRECUENCIAS AGRUPADAS DE DATOS POR
INTERVALOS
Cuando se tiene una gran cantidad de datos numéricos, la distribución
de frecuencia simple resulta larga y difícil de leer, por ello, se recomienda
agruparlos en categorías llamadas intervalos de clase, y elaborar tablas que
muestren la información en una forma más eficiente que permita averiguar
rápidamente su comportamiento, sin embargo, al considerar intervalos de
clase se tiene la desventaja de perder el valor original e individual de cada
uno de los datos.
Antes de iniciar con la construcción de una tabla de distribución de
frecuencia de este tipo, mostraremos el contenido de las columnas básicas
que la forman:
CLASES o INTERVALOS
f
Mc
Límite inferior-Límite superior frecuenci Marca de clase o
o Frontera inf.- Frontera sup. a de
Punto medio
cada
clase
La siguiente gráfica te permitirá visualizar la frecuencia, el número de
intervalos, la amplitud y la marca de clase:
Número de intervalos= número de barras=K=
5
15
Amplitud = ancho de cada columna= A
(todas tienen la misma amplitud)
10
5
Frecuencia= Frecuencia de clase = f
Es la altura de cada barra
0
25
35
45
55
65
Marca de clase= Mc
Punto medio de cada barra
Cada una de las clases o intervalos se encuentra formada por dos
límites llamados aparentes que son el límite inferior(o frontera inferior) y el
límite superior (o frontera superior), es necesario calcular el número de
intervalos al cual llamaremos K, con la única condición de que todos los
datos queden incluidos en los intervalos considerados; la distancia entre los
100
Estadística Descriptiva
límites inferior y superior de un intervalo recibe el nombre de amplitud y se
denota con la letra A.
La frecuencia de cada clase (f) se obtiene al contar el número de datos
que caen dentro de cada intervalo.
La marca de clase o punto medio (Mc) es el número que se obtiene al
dividir la suma de los límites inferior y superior entre dos, dando como
resultado un valor que se encuentra a la mitad de los límites considerados.
7) Apoyados por estos conceptos procedamos a la elaboración de una
tabla de distribución de frecuencia agrupada por intervalos tomando los
datos de un Archivo en donde se quiere conocer el promedio de
expedientes que se presta, considerando una muestra de 50 días al azar.
El número de libros o expedientes prestados durante los 50 días
considerados son:
61
64
62
60
65
50
54
57
63
56
65
65
75
56
57
70
67
53
53
58
45
48
58
61
55
60
64
59
62
51
80
56
56
69
43
65
60
54
70
79
60
61
67
44
72
65
62
68
47
48
Esta información la proporcionó el encargado del Departamento de Control Escolar.
Primero se ordenan los datos de menor a mayor.
43
44
45
47
48
48
50
51
53
53
54
54
55
56
56
56
56
57
57
58
58
59
60
60
60
60
61
61
61
62
62
62
63
64
64
65
65
65
65
65
67
67
68
69
70
70
72
75
79
80
37
Notemos que el dato mayor es 80 y el menor 43 y que es fácil ubicarlo
sólo después de haber ordenado en forma ascendente a todos los
elementos de la muestra.
En Estadística se acostumbra utilizar la letra equis mayúscula “X” para
que represente a un dato, por lo que una vez ordenados se determina el
recorrido o rango, es decir, la diferencia entre el dato mayor y el menor;
utilizando la letra X para representar a estos dos datos se tiene lo siguiente:
Rango o Recorrido = R
R = X máxima - X mínima
R = X máx - X mín
R = 80 - 43 = 37
Como siguiente paso se calcula el número de intervalos, donde
intervalo es cada una de las partes iguales en que se divide el rango. No
olvidemos que cada intervalo está formado por límites superior e inferior en
la columna de clases y se representa con la letra K.
K= número de intervalos
El número de intervalos en una tabla de distribución para datos
agrupados no debe ser muy grande ni muy pequeña sino suficiente para
contener toda la información.
El autor Howard B. Christensen en su libro Estadística Paso a Paso
sugiere una regla llamada de Sturges para establecer el número de
intervalos de acuerdo con el número de datos:
Número de valores en el conjunto
10 a 100
100 a 1000
1000 a 10000
Número apropiado de intervalos
4a8
8 a 11
11 a 14
Para calcular el número de intervalos de una tabla de distribución para
datos agrupados, se puede utilizar nuevamente la Regla de Sturges que
indica que K= 1+ 3.322 x log (n) donde:
n es el tamaño de la muestra
1 y 3.322 son dos valores constantes que nunca cambian
log (n) es el logaritmo de n
En el ejemplo que nos ocupa tenemos que n=50, obteniendo en la
calculadora el valor que le corresponde al log(50) se tiene que es 1.69.
38
Estadística Descriptiva
Sustituyendo estos valores en la fórmula:
K = l + 3.322 x (1.69)
Al resolver primero se multiplica 3.322 por el resultado del logaritmo y
al valor que se obtiene se le suma 1, con lo cual K = 1 + 3.322 x (1.69) =1 +
5.64 = 6.64.
Como el número de intervalos debe ser entero porque representa al
número de barras en una gráfica como la que aparece al inicio de esta
unidad, se debe redondear de la siguiente manera: Si el primer dígito
decimal es mayor o igual que .5 entonces K será igual al valor entero
siguiente, si por el contrario el dígito decimal es menor que .5 entonces K
tendrá el valor del entero anterior, por ejemplo si se obtiene 5.8 K=6 y si se
tiene 7.2 entonces K=7.
En este caso K=7 porque el valor obtenido fue 6.64. Es importante
hacer notar que esta Regla no es infalible y que si en un momento dado se
quiere considerar otro número de intervalos diferente al obtenido, se puede
hacer, con la única condición de que todos los datos de la muestra queden
contenidos en los intervalos.
Después de obtener K, se calcula la amplitud de los intervalos
realizando la división del rango entre el número de intervalos de la siguiente
manera:
R
A= --------K
37
A= ------- = 5.2
7
La amplitud también es un número entero por lo que A se redondea a
5.
Hasta ahora hemos obtenido R= 37, K=7 y A=5, con esta información
ya estamos preparados para construir la tabla de distribución. ¡Adelante!
Escribimos como primer encabezado CLASES y anotamos como
primer límite inferior el valor más pequeño o si desea un valor cercano como
puede ser 40, 41 ó 42; en este caso, consideraremos al 43 que es el dato
menor, para encontrar el segundo límite inferior se le suma la amplitud que
es 5 y así sucesivamente hasta tener 7 intervalos que es el valor de K.
39
A=5
CLASES
43
48
53
+5=
+5=
58
63
68
73
1)
2)
3)
K
4)
5)
6)
7)
Número de clases o intervalos =
K=7
Para realizar el cálculo de los límites superiores o fronteras superiores,
se procede de la siguiente manera: Al primer límite inferior se le suma lo
que vale la amplitud menos 1, esto es, 4 y el resultado es el primer límite
superior, de esta forma se continúa hasta completar los 7 intervalos
considerados en este caso:
Límites aparentes:
límite inferior
límite inferior
CLASES
43- 47
48- 52
53- 57
58- 62
63- 67
68- 72
73- 77
límite superior
límite superior
A los límites o fronteras inferior y superior que acabamos de encontrar
se les llama límites aparentes, existen otros límites que no aparecen en la
tabla pero que también es necesario que conozcas, son los límites reales,
también llamados verdaderos, los cuales se calculan muy fácilmente:
a) A cada límite inferior se le resta .5 y se obtienen los límites reales o
verdaderos.
b) Se agrega .5 a cada límite superior para obtener el límite superior
real o verdadero de cada clase.
límite inferior
aparente
43
48
53
58
63
68
73
40
límite inferior real o
verdadero
42.5
47.5
52.5
57.5
62.5
67.5
72.5
límite superior
aparente
47
52
57
62
67
72
77
límite superior real
o verdadero
47.5
52.5
57.5
62.5
67.5
72.5
77.5
Estadística Descriptiva
Límites reales o verdaderos:
límite inferior real o
verdadero
42.5
47.5
52.5
57.5
62.5
67.5
72.5
límite superior real o
verdadero
47.5
52.5
57.5
62.5
67.5
72.5
77.5
Como verás, para construir la columna de las clases o intervalos de
clase se utilizaron Rango (R), número de intervalos (K) y amplitud (A).
Para llenar la columna de frecuencias absolutas o simplemente f, se
maneja la lista ordenada de los datos, contando el número de los que caen
dentro de cada intervalo, por ejemplo en el primer intervalo 43-43 caen: 43,
44, 45, 47, lo cual significa que tiene frecuencia 4. En esta forma se
continúa hasta tener el total de datos incluidos en los intervalos. Para
verificar que el conteo fue correcto, se suman todas las frecuencias y su
resultado debe ser el tamaño de la muestra que en este caso es 50.
CLASES
43- 47
48- 52
53- 57
58- 62
63- 67
68- 72
73- 77
TOTAL:
f
4
4
11
13
10
5
3
50
Al tener datos agrupados se pierde la individualidad de cada uno, es
por esta razón que se calcula el punto medio o marca de clase, el cual
representa a todos los datos que caen en cada uno de los intervalos.
La marca de clase se calcula en cada intervalo sumando sus límites y
dividiendo entre 2:
límite inferior + límite superior
Mc = ---------------------------------------2
41
CLASES
43- 47
48- 52
53- 57
58- 62
63- 67
68- 72
73- 77
TOTAL:
f
4
4
11
13
10
5
3
50
Mc
45
50
55
60
65
70
75
Esta es la tabla de distribución de frecuencia agrupada de
datos por intervalos.
Existen algunas consideraciones sobre la elaboración de una tabla de
este tipo:
1.- Se sugiere que la amplitud de los intervalos sea impar como en este
caso, ya que de esta forma, se asegura que el punto medio sea entero, en
caso contrario se tendrán decimales.
2.- No es necesario utilizar la Regla de Sturges para el cálculo de K, tú
puedes manejar el número de intervalos que consideres suficientes.
3.- La marca de clase o punto medio representan al número total de
datos que caen en cada intervalo.
A esta tabla se le pueden agregar más columnas como las siguientes:
CLASES
43- 47
48- 52
53- 57
58- 62
63- 67
68- 72
73- 77
TOTAL:
f
4
4
11
13
10
5
3
50
Mc
45
50
55
60
65
70
75
fa
fr
far
La columna de fa o frecuencias acumuladas tiene como primer dato el
que aparece en la columna f que es 4, se le suma la siguiente frecuencia
que también es 4 y se obtiene 8 que es el número que aparece en el
siguiente renglón y así hasta terminar con todas las frecuencias:
42
Estadística Descriptiva
f
4
4
11
13
10
5
3
fa
4
8
19
32
42
47
50
La última frecuencia acumulada (fa) es el tamaño de la muestra.
La columna de frecuencia acumulada es sumamente importante, para
entenderla mejor regresemos a la lista ordenada de datos y coloquemos a
cada uno de ellos el número que le corresponde por su posición ordenada.
1.- 43
2.- 44
3.- 45
4.- 47
5.- 48
6.- 48
7.- 50
8.- 51
9.- 53
10.- 53
11.-54
12.- 54
13.-55
14.-56
15.-56
16.-56
17.-56
18.-57
19.-57
20.-58
21.- 58
22.-59
23.- 60
24.- 60
25.- 60
26.- 60
27.- 61
28.- 61
29.- 61
30.- 62
31.- 62
32.- 62
33.- 63
34.- 64
35.- 64
36.- 65
37.- 65
38.- 65
39.- 65
40.- 65
41.- 67
42.- 67
43.- 68
44.- 69
45.- 70
46.- 70
47.- 72
48.- 75
49.- 79
50.- 80
Con la información de la columna fa se puede ubicar en un intervalo
desde el primer número que cae hasta el último según su posición en la lista
ordenada en forma ascendente.
CLASES
43- 47
48- 52
53- 57
58- 62
63- 67
68- 72
73- 77
fa
4
8
19
32
42
47
50
La columna fa indica que los primeros 4 datos caen en este
intervalo
En esta clase caen desde el dato que ocupa el 5o. lugar hasta el
8vo.
Aquí caen los datos desde el lugar 9o. hasta el 19vo.
De esta forma la columna de frecuencias acumuladas nos proporciona
información sobre los datos que caen en determinado intervalo de clase, por
ejemplo para saber en qué intervalo cae el dato que ocupa el lugar 30, lo
buscamos en fa y aseguramos que cae en el intervalo 58-62 ya que éste
contiene a los datos que ocupan desde el lugar 20 hasta el lugar 32.
43
La columna fr es la frecuencia relativa de cada intervalo, se calcula en
cada intervalo dividiendo su frecuencia entre el tamaño de la muestra,
obteniéndose una razón que se puede escribir de tres formas diferentes.
f
4
4
11
13
10
5
3
50
fr
(fracción)
4/50
4/50
11/50
13/50
10/50
5/50
3/50
50/50
fr
(decimal)
.08
.08
.22
.26
.20
.10
.06
1
fr %
(porcentaje)
8
8
22
26
20
10
6
100
En este último renglón se encuentra la suma de cada columna, es
preciso hacer hincapié en que los tres resultados de las columnas fr son los
mismos, esto significa entonces que fr se puede escribir de cualquiera de
las tres maneras sólo que la última que está en porcentaje es la que más
se utiliza para el tema de gráficas.
De manera similar que fr se calcula la columna de far (fra) o frecuencia
acumulada relativa en porcentaje, solamente que para ésta se toma como
referencia la columna de fa. Veamos, para calcular el primer valor de far se
efectúa la división de cada renglón de fa entre el tamaño de la muestra y el
resultado se multiplica por 100 para tenerlo en porcentaje.
fa
4
8
19
32
42
47
50
far %
8
16
38
64
84
94
100
No hay que perder de vista esta columna ya que es muy
importante
por 2 motivos:
1) Se utiliza para encontrar porcentajes
2) Sus valores se acumulan hasta completar el 100%
Con todo lo anterior se tiene la tabla de distribución de frecuencia
agrupada de datos por intervalos:
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS DE DATOS POR INTERVALOS
44
Estadística Descriptiva
NÚMERO DE LIBROS O EXPEDIENTES PRESTADOS
DURANTE 50 DÍAS
PERÍODO ENERO-MARZO 1997
CLASES
f
Mc
fa
fr
far
43- 47
4
45
4
8
8
48- 52
4
50
8
8
16
53- 57
11
55
19
22
38
58- 62
13
60
32
26
64
63- 67
10
65
42
20
84
68- 72
5
70
47
10
94
73- 77
3
75
50
6
100
TOTAL:
50
100
Fuente: Información proporcionada por el Departamento de Control Escolar.
La presentación de una tabla de distribución de frecuencias para datos
agrupados como la anterior no es la única, en ocasiones, algunos autores
muestran sus tablas iniciando con la clase o intervalo mayor hasta llegar al
más pequeño, es obvio que las demás columnas también sufren esta
modificación, observemos:
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS DE DATOS POR INTERVALOS
NÚMERO DE LIBROS O EXPEDIENTES PRESTADOS
DURANTE 50 DÍAS
PERÍODO ENERO-MARZO 1997
CLASES
f
Mc
fa
fr
far
73-77
3
75
50
6
100
68-72
5
70
47
20
94
63-67
10
65
42
20
84
58-62
13
60
32
26
64
53-57
11
55
19
22
38
48-52
4
50
8
8
16
43-47
4
45
4
8
8
50
100
Fuente: Información proporcionada por el Departamento de Control Escolar.
En este caso la columna de frecuencia acumulada se inicia con el
tamaño de la muestra que es 50 y se le va restando la frecuencia hasta
obtener el valor de la primera:
f
3
5
10
13
11
4
4
50
fa
50
47
42
32
19
8
4
50 - 3
45
¿QUÉ HE APRENDIDO?
Es muy importante que recuerdes la forma en que se construye una
tabla de distribución de frecuencias para datos por intervalos, también
llamada para datos agrupados, ya que en tu futuro como profesional de la
información es una herramienta que te será de gran utilidad.
1) Escribe claramente tus propias definiciones de Rango, Amplitud y
Número
de
intervalos.
________________________________________________________
____________________________________________________________
________
2) ¿Qué diferencias encuentras entre frecuencia absoluta (f) y
frecuencia
relativa
(fr)?
_________________________________________________________
____________________________________________________________
________
3) ¿Por qué es importante la columna de frecuencias acumuladas (fa)?
Explica
tu
respuesta.
_________________________________________________________
____________________________________________________________
________
46
Estadística Descriptiva
Elabora el Resumen de la Unidad 2 completando el siguiente mapa
conceptual, al final de la guía lo encontrarás resuelto, de ser posible,
confronta tus respuestas y corrígelas en caso de ser erróneas:
TIPOS DE DATOS
CATEGÓRICOS
ORDENADOS POR RANGO
MÉTRICOS
DISTRIBUCIONES DE FRECUENCIA
POBLACIÓN O MUESTRA PEQUEÑA
SIMPLE CUYA ESTRUCTURA ES:
a)
b)
c)
d)
A
B
f
f
SUMA DE f
TO T A L
e)
f)
g)
donde:
a) Título que explique brevemente el
contenido de la tabla
b)
c)
d)
e)
f)
g)
POBLACIÓN O MUESTRA GRANDE
PARA DATOS AGRUPADOS CUYA
ESTRUCTURA ES:
a)
b)
c)
d)
e)
f)
donde:
a)Clases o intervalos formados por límite inferior
y límite superior
b)
c)
d)
e)
f)
TIPO DE VARIABLES QUE UTILIZAN
a) ORDINALES
b)
c)
d)
a)
b)
47
EVALUACIÓN
1)Se atendieron en un mes a 40 investigadores en cierta área, si el
mes anterior se habían atendido 80 ¿cuál es el porcentaje de disminución?
____________________________________________________________
________
2) Un empleado atiende 200 personas durante una semana ¿cuántas
personas más deberá atender la próxima para obtener un incremento del
25%?
____________________________________________________________
________
3) Si en el área de Préstamo a domicilio existen 125 volúmenes y en el
área de consulta 375:
a)
¿Cuál
es
la
razón
entre
las
dos
áreas?
______________________________
b) ¿En qué porcentaje es mayor el volumen de consulta con respecto
al
préstamo
a
domicilio?__________________________________________________
4) Si en un Archivo se tienen 50 legajos sobre el Tratado de Libre
Comercio y sobre Posesión de la tierra 100 ¿cuál es la razón entre los
primeros
y
los
segundos?
____________________________________________________________
________
5) Con los datos proporcionados por el Departamento de Control
Escolar de una Universidad,
que representan las horas dedicadas
semanalmente al estudio fuera de clases por los estudiantes que asisten
regularmente, completa la tabla de distribución para datos agrupados,
anotando todo lo que se te solicita:
3
2
5
8
2
5
11
48
11
4
3
15
4
5
16
8
9
20
4
3
12
1
22
6
17
5
2
13
8
7
4
2
15
6
4
14
5
2
10
17
9
2
1
3
18
18
3
6
1
6
Estadística Descriptiva
21
7
1
6
13
10
12
23
11
1
10
3
5
12
10
6
16
1
11
4
12
a) Escribe la variable de interés y el tipo al que pertenece:
________________________________________________________
______
b) ¿Cuál es la población del problema?
________________________________________________________
_______
c) Es población finita o infinita:
________________________________________________________
_______
d) La muestra está formada por ______________ elementos.
e) Ordena los datos en forma ascendente:
f) Calcula y escribe el valor de:
R= Rango =
K= Número de intervalos=
A= Amplitud=
g) Completa la tabla de distribución para datos agrupados indicando
claramente título y fuente según la información proporcionada:
CLASES
f
Mc
fr
fa
far
49
6) En un Archivo diariamente se devuelven en promedio 520
expedientes que fueron solicitados para su consulta y se colocan en el lugar
que les corresponde. Para llevar un control adecuado, semanalmente se
hace una revisión a fin de que la suma de los entregados más los que están
en préstamo nos de el total de expedientes, por lo general de cada 13
expedientes uno se encuentra extraviado, ya sea porque está en préstamo
sin vale o porque está mal colocado, el porcentaje con que se presenta la
primera opción es del 65%. Con esta información realiza las operaciones
necesarias para contestar correctamente:
a) Considerando el promedio de expedientes que se devuelven,
aproximadamente ¿cuántos expedientes devuelven al Archivo durante los 5
días de la semana?
________________________________________________________
_______
b) ¿Aproximadamente cuántos expedientes se extravían a la semana?
________________________________________________________
_______
c) ¿Cuántos expedientes se extravían semanalmente por estar
prestados sin el vale respectivo?
________________________________________________________
_______
d) ¿Cuántos expedientes están extraviados semanalmente por estar
mal colocados?
________________________________________________________
_______
7) En una biblioteca semanalmente (lunes a sábado) se solicita en
préstamo a domicilio un promedio de 830 libros, si cada domingo se hace
una revisión para comprobar que el número de ejemplares prestados más
los que se tienen suman el total disponible para este servicio,
encontrándose que aproximadamente
de cada 20 libros 3 están
extraviados, efectúa las operaciones correspondientes y anota el resultado
en cada inciso:
a) ¿Cuántos libros en promedio se prestan diariamente (de lunes a
sábado)?
50
Estadística Descriptiva
________________________________________________________
_______
b)¿Cuál es la cantidad de libros que se extravían diariamente?
________________________________________________________
_______
c)¿Qué porcentaje de libros se extravían semanalmente?
________________________________________________________
_______
ENVÍA A TU ASESOR
Si has llegado hasta aquí, te felicito, tu esfuerzo tendrá una
recompensa.
51
1st Qtr
2nd Qtr
3rd Qtr
4th Qtr
UNIDAD 3
REPRESENTACIONES
GRÁFICAS
En esta unidad aprenderás a elaborar diferentes gráficas a partir de los
datos contenidos en tablas de distribución de frecuencias, por ello es
necesario que prepares papel milimétrico, compás, regla y transportador.
¿QUÉ VOY A APRENDER EN ESTA UNIDAD?
A trazar gráficas de barras horizontales o verticales y de sectores
cuando se trate de variables cualitativas, y si se tienen datos cuantitativos a
elaborar histogramas y polígonos de frecuencia, ya que al ser presentados
los datos en forma resumida podemos observar gráficamente sus
principales características.
52
Estadística Descriptiva
DIAGNÓSTICO
1) Dibuja el Sistema de Coordenadas Rectangulares o plano
cartesiano indicando el nombre de los ejes, el origen, y los cuadrantes.
2) Para cada inciso traza un plano cartesiano y utilizando sólo el primer
cuadrante marca en ambos ejes las escalas que se te solicitan:
a) Ambos ejes a escala 1:1 hasta 10 (un centímetro equivale a la
unidad).
b)Ambos ejes a escala 1:2 hasta 20, esto es, iniciando en uno y de dos
en dos hasta 20. (un centímetro equivale a 2 unidades).
c) Ambos ejes a escala 1:5 iniciando en 1 y terminando en 50 (un
centímetro equivale a 5 unidades).
53
d) El eje “X” de 1:2 hasta 20 y en el eje “Y” de 1:10 hasta 100.
3) Busca en el diccionario el significado de simetría y dibuja una figura
simétrica.
Si al realizar la actividad diagnóstica tuviste problemas para trazar el
Sistema de Coordenadas Rectangulares mejor conocido como el plano
cartesiano, recordemos que éste se encuentra formado por dos rectas
perpendiculares entre sí, las cuales
reciben el nombre de ejes
coordenados, siendo el horizontal el de las “X” o abscisas y el vertical el de
las “Y” o de las ordenadas, su punto de intersección es el origen.
Sistema de Coordenadas Rectangulares
II
I
eje Y
(o de las ordenadas)
III
origen
(punto 0)
eje X (o de las abscisas)
IV
Los números romanos nos indican los cuadrantes.
En cada uno de los incisos en donde se te solicitan escalas se requiere
trazar el plano cartesiano, los primeros 3 incisos son muy fáciles como lo
viste en Escalas de Medición, sólo veremos el inciso d) en donde se te pide
trazar en el eje “X” una escala de 1:2 hasta 20 y en el eje “Y” de 1: 10 hasta
100:
54
Estadística Descriptiva
100
EJE Y
30
20
10
2
origen
4
6
8
10 12 14
16 18
20
EJE X
Para terminar con la reflexión de esta unidad, no debes olvidar que una
figura es simétrica cuando se divide en dos partes iguales de tal forma que
éstas coinciden al girar una de ellas 180 grados.
Bien, una vez que ya nos familiarizamos con el Sistema de
Coordenadas Rectangulares y recordado lo que significa que una figura sea
simétrica, continuemos con el tema de representaciones gráficas en donde
debes tener en cuenta las siguientes observaciones:
a) Todas las gráficas, menos la de sectores se trazan en el primer
cuadrante del Sistema de Coordenadas Rectangulares.
b) Es indispensable que en todas las gráficas aparezca en primer lugar
un título que describa brevemente la información que está siendo
representada y la fuente de información, ya que éstas deben ser
autoexplicativas, con excepción de la gráfica de sectores, todas deben
contener un título en cada uno de los ejes que indique el tipo de datos que
se están representando.
c) Las gráficas son necesarias y útiles para conocer el comportamiento
de los datos, es por ello que se recomienda tener cuidado tanto en su
elaboración como en su revisión, ya que de lo contrario se podría caer en
interpretaciones erróneas.
55
3.1 GRÁFICA DE BARRAS
N
Ú
M
E
R
O
GRÁFICA DE BARRAS
(HORIZONTAL)
100
50
0
RUSO
ALEMAN
CHINO
ESPAÑOL
IDIOMAS
Conocida también como diagrama de barras, por estar formada por
barras que tienen el mismo ancho y están separadas por espacios en
blanco, los datos deben estar incluidos en unas cuantas categorías
(representadas por los rectángulos o barras), ya que esta gráfica no es
recomendable cuando se tiene una gran cantidad de información.
Consideremos la información de la tabla que aparece enseguida y que
contiene 2 categorías: Archivonomía y Biblioteconomía.
ALUMNOS DE LA ENBA
Semestre 97-I
CARRERA
NÚM.DE ALUMNOS
(X)
(f)
ARCHIVONOMÍA
270
BIBLIOTECONOMÍA
351
Total:
621
Primero trazamos el primer cuadrante del plano cartesiano, en el eje
horizontal se anotan las categorías, en el eje vertical se considera una
escala o división conveniente para marcar las frecuencias respectivas,
posteriormente se trazan barras del mismo ancho y con la misma
separación.
En la actualidad cuando se realizan este tipo de gráficas, sobre todo en
la computadora, se tiene la opción de escoger barras con o sin separación y
horizontales o verticales.
Al trazar las barras se debe tener en cuenta que la separación entre
ellas no debe ser menor que la mitad de su ancho ni mayor que el mismo y
la altura de cada una queda determinada por la frecuencia que le
corresponde, de esta forma cada categoría queda representada por una
columna.
56
Estadística Descriptiva
GRÁFICA DE BARRAS VERTICALES
La información contenida en la tabla anterior de distribución simple
aparece gráficamente en el diagrama:
ALUMNOS INSCRITOS EN LA ENBA
SEMESTRE 97-I
N
Ú
M
E
R
O
D
E
A
L
U
M
N
O
S
400
350
300
250
200
Notemos que se destaca
inmediatamente la categoría de
mayor frecuencia, por lo que en
este caso es claro que la carrera de
Biblioteconomía tiene más alumnos
inscritos que la de Archivonomía.
150
El Autor Luis Magaña Cuéllar
en
su
libro
Estadística
y
0
probabilidad indica que en la
representación gráfica se debe
construir, cada vez que se pueda, el
eje vertical de tal modo que la altura del punto máximo (que representa el
dato asociado a la frecuencia más alta) sea aproximadamente igual a ¾ de
la longitud que media entre el origen y el último dato indicado en el eje
horizontal.
100
50
ARCHIVONOMÍA
BIBLIOTECONOMÍA
CARRERAS
¿Por qué crees que se deba seguir esta regla en la elaboración de
una gráfica?
GRÁFICA DE BARRAS HORIZONTALES
ALUMNOS INSCRITOS EN LA ENBA
SEMESTRE 97-I
BIBLIOTECONOMÍA
CARRERAS
A continuación se muestra la
misma
información
en
un
diagrama de barras horizontales,
en donde se ha cambiado el
papel de los ejes, anotando los
nombres de las categorías en el
eje vertical y las frecuencias en el
eje horizontal:
ARCHIVONOMÍA
0
50
100 150 200 250 300 350 400
NÚMERO DE ALUMNOS
Como
ya
hemos
mencionado las categorías al ser
representadas en una gráfica o diagrama de barras permiten visualizar
fácilmente el comportamiento de los datos.
57
¿QUÉ HE APRENDIDO?
1) Con los datos de la siguiente tabla elabora una gráfica de barras.
OCUPACIÓN DE LAS PERSONAS USUARIAS DE UN ARCHIVO
JUNIO 1997
OCUPACIÓN
NÚM.DE PERSONAS
(X)
(f)
INVESTIGADORES
150
DOCENTES
120
ESTUDIANTES
230
Total:
500
Con la información que aparece en la gráfica calcula:
2) La proporción entre docentes y estudiantes.
________________________________________________________
____________________________________________________________
____________________________________________________________
_______________________
3) El porcentaje de investigadores con respecto a la población.
________________________________________________________
____________________________________________________________
58
Estadística Descriptiva
____________________________________________________________
_______________________
59
3.2 GRÁFICA DE SECTORES
Como primer punto recordemos dos definiciones que son importantes
para comprender mejor la forma en que se elabora una gráfica de este tipo:
Circunferencia: curva plana y cerrada, todos los puntos que la forman
están a la misma distancia del centro.
Círculo: superficie plana limitada por la circunferencia.
En seguida, veamos un ejemplo en donde es claro observar que a
cada categoría se le asocia un sector o “gajo” proporcional de la
circunferencia, el cual depende de su frecuencia.
GRÁFICA DE SECTORES
ALEMÁN
13%
RUSO
18%
ESPAÑOL
45%
CHINO
24%
Para la construcción de esta gráfica no se requiere el trazo del plano
cartesiano, en su lugar, se dibuja una circunferencia donde, como ya dijimos
anteriormente, a cada categoría le va a corresponder un sector del círculo.
A fin de contar con toda la información necesaria para trazar esta
gráfica, se recomienda elaborar una tabla auxiliar que contenga todos los
datos que se requieren.
Consideremos nuevamente la tabla de distribución de frecuencias
simple:
ALUMNOS DE LA ENBA
SEMESTRE 97-I
X
f
%
ARCHIVONOMÍA
270
BIBLIOTECONOMÍA
351
621
60
GRADOS
Estadística Descriptiva
Aparecen dos columnas adicionales: En una de ellas se anota el
porcentaje que le corresponde a cada categoría con respecto a la población
(o muestra), y en la otra se anotan los grados que servirán para la medición
del ángulo de cada sector, sin olvidar que todas las circunferencias abarcan
un ángulo de 360 grados.
Para el cálculo del porcentaje se realiza el siguiente procedimiento en
cada categoría:
Al total se le considera el 100%, en este caso como N=621
621
100%
Estas dos cantidades permanecen constantes al efectuar el cálculo en
todas las categorías.
La primera categoría tiene una frecuencia de 270 y desconocemos el
porcentaje que le corresponde con respecto al total, si asignamos con una
letra “a” el valor desconocido y escribimos:
621
270
100%
a
Este planteamiento corresponde a una regla de tres simple, ya que
consta de 4 términos donde 3 son conocidos y uno desconocido. Esta se
resuelve en cruz de la siguiente manera:
621
270
100%
a
El término desconocido “a” es igual al producto de 270 por 100 entre
621.
a= (270x100)/621=43.4 entonces el porcentaje que le corresponde a
270 es 43.4%.
Cuando se tienen números decimales como en este caso, es
conveniente redondear hasta el entero o decimal más próximo tomando en
consideración los siguientes criterios:
a) Aproximación a un entero
9.2 = 9
9.8 = 10
4.5 = 5
Si el último dígito de un número es menor que 5, se redondea al entero
inmediato inferior como en el primer ejemplo que se muestra, en caso de
61
que el dígito de que se trata sea mayor o igual a 5 se considera el entero
inmediato superior.
b) Aproximación a la décima
3.17 =3.2
5.11 =5.1
0.09 =0.1
c) Aproximación a la centésima 6.177=6.18
0.674=0.67
2.098=1.10
En estos dos incisos se observa que si el último dígito es menor que 5,
no se toma en cuenta y si el último dígito es mayor que 5, el anterior se
aumenta en una unidad. Cuando la parte decimal de un número termina en
5 es necesario considerar el dígito anterior:
d) Si es impar, se incrementa en una unidad
7.875 =7.88
18.755 =18.76
e) Si es par se redondea conservando el penúltimo dígito
2.25 = 2.2
8.05 = 8.0
Ahora calculemos el porcentaje de la siguiente categoría
621
351
a=(351x100)/621=56.5,
corresponde el 57%
redondeando
100%
a
se
tiene
que
a
351
le
Los valores obtenidos se anotan en la columna de porcentaje (%)
X
ARCHIVONOMÍA
BIBLIOTECONOMÍA
f
270
351
621
%
43
57
GRADOS
En la última columna se anotan los grados calculados con la regla de
tres simple para cada categoría:
62
Estadística Descriptiva
Cabe hacernos en este momento una pregunta ¿Si a N=625 le
corresponden
360 grados, cuántos le corresponden a 270? Para
responder, planteamos una regla de 3 simple y la resolvemos:
621----- 360 grados
270 ------ a
a = (270(360))/621= 156.52, la fracción .52 se transforma a minutos, es
decir, se multiplica .52 por 60.
.52(60) = 31.2
Redondeando el valor obtenido se tienen 31 minutos, esto indica que a
la primera categoría le corresponden 156 grados con 31 minutos.
Efectuemos la misma operación para el cálculo de los grados de la
siguiente categoría que tiene una frecuencia de 351:
621 ----- 360 grados
351 ------ a
a = (351(360))/621 = 203.47, realizando la misma transformación de la
parte decimal:
.47(60) = 28.2
Al redondear se obtienen 28 minutos, por lo que a la segunda
categoría le corresponden 203 grados con 28 minutos.
Ya estamos en condiciones de completar la tabla:
X
ARCHIVONOMÍA
BIBLIOTECONOMÍA
f
%
270
351
621
43
57
100
GRADO
S
156°31′
203°28′
359°59′
Es recomendable obtener el total de las columnas de porcentaje y de
grados para verificar que los cálculos están correctos, en algunos casos
debido al redondeo no se llega al 100% ni a 360 grados, sin embargo, no te
preocupes si obtienes como mínimo 99% ó 359 grados los resultados están
correctos y son aceptables.
Con los datos obtenidos se realiza el trazo de la gráfica circular o de
sectores en la forma que se indica:
63
1) Se dibuja una circunferencia y el radio vertical principal y a partir de
éste, en el sentido de las manecillas del reloj se miden con un transportador
los grados que le corresponden a cada categoría:
À
2) Como indica la flecha se miden los grados que se calcularon,
iniciando con el valor más grande hasta llegar al más pequeño. Conforme
se marcan los grados en la circunferencia, se van trazando los radios que
formarán los sectores de la gráfica.
3) Los grados no aparecen en la gráfica, ya que sólo se utilizan para
marcar el sector que le corresponde a cada categoría.
ALUMNOS DE LA ENBA
SEMESTRE 97-I
ARCHIVONOMÍA
43%
BIBLIOTECONOMÍA
57%
Aquí aparecen todas las categorías con su porcentaje respectivo, el
cual ha sido calculado tomando en cuenta el tamaño de la muestra (o
población).
Se observa que la Carrera de Biblioteconomía presenta un porcentaje
mayor de alumnos inscritos.
64
Estadística Descriptiva
¿QUÉ HE APRENDIDO?
1) Completa la tabla siguiente y elabora la gráfica de sectores
correspondiente:
OCUPACIÓN DE LOS USUARIOS DE UN ARCHIVO
JUNIO 1997
OCUPACIÓN
NÚM.DE
%
(X)
PERSONAS
GRADO
(f)
S
INVESTIGADORES
150
DOCENTES
120
ESTUDIANTES
230
Total:
500
Con la información de la gráfica que acabas de elaborar contesta:
2) La categoría que tiene mayor porcentaje es :
________________________________________________________
____________________________________________________________
_______________
3) El porcentaje de la categoría que tiene menor frecuencia es:
________________________________________________________
____________________________________________________________
_______________
65
Nota: No olvides que el total de la columna del porcentaje debe estar entre 99 y 101% y la
que corresponde a los grados entre 359 y 361 grados.
66
Estadística Descriptiva
3.3 HISTOGRAMA DE FRECUENCIAS ABSOLUTAS
Es la representación gráfica de una tabla de frecuencias para datos
cuantitativos agrupados y se construye trazando en el primer cuadrante del
plano cartesiano rectángulos unidos, donde los intervalos de clase
determinan el ancho de cada uno de los rectángulos y las frecuencias
sus alturas correspondientes.
Si se consideran las frecuencias absolutas el gráfico recibe el nombre
de Histograma de frecuencias absolutas o simplemente de frecuencias, si
se consideran las frecuencias relativas se trata de un Histograma de
frecuencias relativas.
FRECUENCIAS
ABSOLUTAS
HISTOGRAMA DE FRECUENCIAS
ABSOLUTAS
14
12
10
8
6
4
2
0
3
4
7
10
13 16 19 22 25
MARC AS DE CLASE
Para construir un histograma como el anterior utilizaremos la
distribución de frecuencias para datos agrupados de la Unidad 2:
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS DE DATOS POR INTERVALOS
NÚMERO DE LIBROS O EXPEDIENTES PRESTADOS
DURANTE 50 DÍAS
PERÍODO ENERO-MARZO 1997
CLASES
43- 47
48- 52
53- 57
58- 62
63- 67
68- 72
73- 77
f
4
4
11
13
10
5
3
50
Mc
45
50
55
60
65
70
75
fa
4
8
19
32
42
47
50
fr
8
8
22
26
20
10
6
100
far
8
16
38
64
84
94
100
67
Los datos que se toman en cuenta para trazar el histograma son las
marcas de clase de cada intervalo y sus frecuencias absolutas (f):
Mc
45
50
55
60
65
70
75
f
4
4
11
13
10
5
3
50
Ya estamos listos para efectuar el trazo del histograma de frecuencias
absolutas:
1) Se dibuja el primer cuadrante del plano cartesiano.
2) A fin de mostrar que se ha considerado el origen se inserta una
marca de rompimiento:
eje Y
marca de rompimiento
origen
eje X
La marca de rompimiento evita que tengamos que marcar en el eje
horizontal desde el “cero” que es el origen hasta la primera marca de clase
que es 45.
3) A lo largo del eje horizontal o de las “X” se trazan las marcas de
clase, tomando en cuenta que la gráfica debe quedar equilibrada (o
centrada), por lo que es necesario dejar el mismo espacio antes de la
primera marca de clase y después de marcar la última (es opcional).
45
50
55
60
65
70
75
Estas dos distancias deben ser iguales y mayores que la longitud que
separa una marca de clase con otra.
68
Estadística Descriptiva
4) Sobre el eje vertical trazar una escala adecuada que permita ubicar
las frecuencias de cada intervalo, en este caso si el valor más pequeño es 3
y el mayor 13, se puede considerar una escala de 2 en 2:
.
.
.
6
4
2
0
45
50
55 60 ...
Es conveniente que la escala se tome de acuerdo a los valores
extremos, ya que si se presenta un caso en que el valor mínimo es 20 y el
máximo 100, se tiene la opción de escoger una escala de 5 en 5 o de 10 en
10 o cualquier otra que no tenga valores tan pequeños como la anterior.
5) Es importante anotar títulos, uno principal que especifique en forma
clara y breve la información que contiene el histograma y en cada uno de
los ejes para indicar lo que se está graficando. También es necesario anotar
la fuente de la información.
EXPEDIENTES PRESTADOS
PERÍODO ENERO-MARZO 1997
14
12
10
DÍAS 8
6
4
2
0
40
45
50
55
60
65
70
75
80
NÚMERO DE EXPEDIENTES
Fuente: Información proporcionada por el Departamento de Control Escolar.
Información que muestra el histograma:
1)La barra más alta tiene una altura de 13 y corresponde a la marca de
clase 60, esto significa que durante 13 días se prestaron en promedio 60
expedientes.
69
2) Durante 4 días se prestaron en término medio 45 expedientes y en
el mismo número de días se prestaron 50 expedientes.
3) El máximo número de expedientes que son 75 se prestaron durante
3 días.
4) El área de cada rectángulo, en relación con los restantes, muestra la
proporción del número total de observaciones que ocurren en cada clase.
5) Al estar los datos agrupados se pierde la información individual de
cada uno, pero se tiene una visión general de la distribución de los mismos.
6) Al intervalo que le corresponde la barra con mayor número de datos
o más alta, se le llama clase modal, en este caso es 58-62.
LECTURA 2
Con el propósito de que conozcas un poco más sobre los diferentes
tipos de gráficas, es necesario que leas del
Capítulo 3 del libro
Fundamentos de Estadística en la Investigación Social de Jack Levin
incluido al final de esta guía y elabores un breve resumen para reafirmar tu
aprendizaje.
Después de la lectura continúa con más ímpetu el desarrollo de esta
unidad.
Las formas de los histogramas
continuación:
70
más comunes se muestran a
Estadística Descriptiva
HISTOGRAMA SIMÉTRICO
Presentan a la clase de mayor
12
10
8
6
4
HISTOGRAMA ASIMÉTRICO
A LA DERECHA
2
0
25
35
45
55
65
12
10
8
6
4
2
0
frecuencia o clase modal a la mitad
del histograma.
Se observan dos colas, la más
25
35
45
55
65
pequeña a la izquierda y la mayor
hacia la derecha del intervalo de
mayor frecuencia. Si con esta misma información se considera el polígono
de frecuencias absolutas tendremos una distribución con sesgo hacia la
derecha (se considera positivo).
La cola más larga se extiende hacia la izquierda de la clase mayor, de
igual manera si consideramos su
polígono de frecuencia respectivo, se
tiene una distribución sesgada hacia la
HISTOGRAMA ASIMÉTRICO
izquierda.
A LA IZQUIERDA
12
10
8
6
4
2
HISTOGRAMA
RECTANGULAR
0
25
35
45
55
65
12
10
8
6
4
2
0
25
35
45
55
65
71
Todas las categorías tienen la misma frecuencia.
No se observa ninguna cola
en el lado donde se encuentra la
categoría con mayor frecuencia.
HISTOGRAMA EN FORMA DE
"J"
12
NOTA: Estas gráficas se elaboraron
en computadora y no aparecen espacios en
blanco, antes y después del primer y último
rectángulo.
10
8
6
4
2
0
25
35
45
55
65
¿QUÉ HE APRENDIDO?
1) Completa la siguiente tabla que contiene los retardos en minutos
que 50 personas tuvieron en un mes.
CLASES
5- 9
10-14
15-19
20-24
25-29
f
10
8
15
5
12
50
Mc
2) Anota el intervalo que tiene mayor frecuencia, el cual por esta razón
recibe
el
nombre
de
clase
modal:______________________________________________
3) Con la información de la tabla elabora el histograma de frecuencias
absolutas correspondiente y destaca la barra más alta o de mayor
frecuencia.
72
Estadística Descriptiva
4) Compara la forma que presenta el histograma con las que se
mostraron
anteriormente
y
escribe
a
qué
categoría
corresponde:________________________
____________________________________________________________
________
73
3.4 POLÍGONO DE FRECUENCIAS ABSOLUTAS
Es una gráfica lineal que muestra los datos que contiene una
distribución de frecuencia para datos agrupados, en el eje X se colocan las
marcas de clase y en el eje “Y” las frecuencias. Se unen los puntos medios
de cada clase a la altura de su frecuencia correspondiente.
POLÍGONO DE FRECUENCIAS
ABSOLUTAS
FRECUENCIAS
ABSOLUTAS
12
10
8
6
4
2
0
1
4
7
10
13
16
19
22
25
MARCAS DE CLASE
Recordemos que un polígono es una figura plana limitada por rectas
que forman una línea quebrada cerrada, por ello, es necesario agregar una
marca de clase al principio y otra al final, ambas con frecuencia cero “0” a
fin de cerrar la poligonal.
Veamos nuevamente las columnas que se usaron para la elaboración
del Histograma de frecuencias absolutas:
Mc
40
45
50
55
60
65
70
75
80
f
0
4
4
11
13
10
5
3
0
50
Parte más alta o “pico”
74
Estas dos marcas de clase con frecuencia “0”
se agregaron para cerrar la curva.
Estadística Descriptiva
EXPEDIENTES PRESTADOS
PERÍODO ENERO-MARZO 1997
14
12
10
DÍAS
8
6
4
2
0
35 40 45 50 55 60 65 70 75 80 85
NÚMERO DE EXPEDIENTES
Es importante observar que la curva comienza en el punto medio de la
clase anterior a 45 y termina en el punto medio de la clase posterior a la
última, de no ser así, sólo se tendría una poligonal.
Información que muestra el polígono:
1) El área total bajo la curva es igual al área total bajo el histograma
correspondiente.
2) Muestra un esquema más claro del comportamiento de los datos,
como por ejemplo, su parte más alta corresponde a la mayor frecuencia.
3) Si sólo presenta un “pico”, como en este ejemplo, significa que su
categoría correspondiente contiene el dato que se repite más veces.
4) En caso de que se observe más de un “pico” se tienen varios datos
con frecuencia mayor (o muy parecida).
NOTA: También se puede utilizar la columna de frecuencias relativas (fr) en lugar de la de
frecuencias absolutas y graficarse para obtener un polígono de frecuencias relativas.
75
¿QUÉ HE APRENDIDO?
1) A continuación se muestran las edades de 55 trabajadores de cierta
empresa, completa la tabla:
CLASES
20-29
30-39
40-49
50-59
2)
Escribe
la
clase
________________________
modal
f
25
10
15
5
55
Mc
o
de
mayor
frecuencia
3) ¿En qué intervalo se encuentran agrupados los empleados más
jóvenes?
____________________________________________________________
________
4) Traza el polígono de frecuencias respectivo.
76
Estadística Descriptiva
3.5 POLÍGONO DE FRECUENCIAS RELATIVAS ACUMULADAS
U OJIVA PORCENTUAL
También conocido como Polígono de frecuencias acumuladas
relativas, es una curva que representa el área proporcional relativa
acumulada en cada clase y permite calcular de manera visual las
proporciones de sus valores que se acumulan al final de cada clase, en
otras palabras muestra gráficamente cuántas observaciones se encuentran
por arriba o debajo de ciertos valores, en lugar de limitarnos a conocer el
número de elementos que caen dentro de cada uno de los intervalos.
Algunos autores como Agustín Montaño en su libro Estadística I,
utilizan en el eje de las “X” las marcas de clase y otros como Jack Levin en
su libro Fundamentos de Estadística en la Investigación Social usan en el
mismo eje los límites reales superiores de cada intervalo.
No hay por qué preocuparse, ambas formas tienen el mismo propósito
y no hay mayor problema en considerar marcas de clase o límites reales
superiores.
Utilizando la misma información se ha trazado una gráfica con cada
uno de ellos:
OJIVA PORCENTUAL CON MARCAS DE CLASE EN EL EJE DE LAS
“X”:
FRECUENCIAS
RELATIVAS
ACUMULADAS (%)
POLÍGONO DE FRECUENCIAS RELATIVAS
ACUMULADAS U OJIVA PORCENTUAL
100
80
60
40
20
0
10
15
20
25
30
35
40
MARCAS DE CLASE
77
OJIVA PORCENTUAL CON LÍMITES REALES SUPERIORES EN EL
EJE DE LAS “X”
FRECUENCIAS
RELATIVAS
ACUMULADAS (%)
POLÍGONO DE FRECUENCIAS RELATIVAS
ACUMULADAS U OJIVA PORCENTAL
100
80
60
40
20
0
12.5 17.5 22.5 27.5 32.5 37.5 42.5
LÍMITES REALES SUPERIORES
A simple vista se observa que la forma de las dos ojivas es la misma,
veamos que sucede cuando consideramos un problema y obtenemos su
polígono de frecuencias acumuladas en las dos formas descritas
anteriormente.
Durante un mes se tomaron las temperaturas en una bóveda donde se
guardan expedientes, obteniéndose las siguientes lecturas: 3, 12, 21, 30,
15, 24, 6, 15, 21, 3, 15, 21, 3, 18, 24, 12, 27, 6, 9, 6, 27, 18, 18, 9, 27, 6, 30,
18, 24 y 9 grados respectivamente.
Primero se ordenan los datos:
3
3
3
6
6
6
6
9
9
9
12
12
15
15
15
18
18
18
18
21
21
21
24
24
24
27
27
27
30
30
R=30-3 = 27
K= 1 + 3.322(log 30) = 1 + 3.322(1.47) = 5.9 redondeando K=6
A= 27/6 = 4.5 al redondear A=5
CLASES
3-7
8-12
13-17
18-22
23-27
28-32
78
f
7
4
3
7
7
2
30
Mc
5
10
15
20
25
30
fa
7
11
14
21
28
30
far
23
37
47
70
93
100
Estadística Descriptiva
OJIVA PORCENTUAL CON MARCAS DE CLASE EN EL EJE DE LAS
“X”
Para
estimar
el
porcentaje
de
temperaturas menores de
20 grados, localizamos la
frecuencia
acumulada
relativa que se intersecta
con este dato.
TEMPERATURAS LEÍDAS DURANTE UN MES EN UN
ARCHIVO
FRECUENCIA ACUMULADA
RELATIVA (%)
100
90
80
70
60
50
40
30
20
10
0
5
10
15
20
TEMPERATURAS
25
30
Así encontramos que
aproximadamente el 70%
del total de datos es
menor que 20, para
verificarlo veamos cuántos
números son menor de
20:
3,3,3,6,6,6,6,9,12,12,15,15,15, 18, 18, 18, 18 (un total de 17 datos que
representan un 56.6%)
Al calcular el 70% del total de 30 datos, obtenemos 21 datos, cantidad
que es ligeramente mayor que el número de datos listados anteriormente.
De igual manera si deseamos saber cuántas temperaturas del mes
considerado fueron mayores de 25 grados, veremos que las menores
fueron aproximadamente el 92%, por lo tanto, las mayores tienen un
porcentaje del 8% es decir, que aproximadamente de 2 a 3 lecturas son
mayores de 25 grados.
Nuevamente, de la lista de datos ordenada tenemos que los grados
mayores a 25 son: 27, 27, 27, 30, 30, estos 5 datos representan el 16.6%
de todas las temperaturas.
En ambas estimaciones existe diferencia entre los porcentajes
obtenidos a través de la gráfica y los calculados con los datos
proporcionados inicialmente.
79
OJIVA PORCENTUAL CON LÍMITES REALES SUPERIORES EN EL
EJE DE LAS “X”
Realicemos la misma estimación de porcentajes que en la anterior
gráfica:
FRECUENCIAS
ACUMULADAS RELATIVAS
(%)
TEMPERATURAS LEÍDAS DURANTE UN MES EN UN
ARCHIVO
100
90
80
70
60
50
40
30
20
10
0
7.5
12.5
17.5
22.5
27.5
32.5
TEMPERATURAS
Primero observemos que 20 grados se localiza a la mitad de 17.5 y
22.5, para estimar el porcentaje de temperaturas mayores de esta cantidad
vemos que en el eje de las “Y”, la frecuencia acumulada relativa que le
corresponde es 60%, lo cual implica que 18 datos (el 60% de 30) son
mayores de 20, este valor es más cercano que el que se obtuvo en la
anterior ojiva.
Ahora para conocer el número de datos mayores de 25 grados,
localiza esta temperatura en el eje de las “X”, el cual se encuentra a la mitad
de 22.5 y 27.5 y le corresponde un porcentaje del 80%, entonces podemos
decir que la estimación de valores mayores de 25 es 20%, esto es, 6 datos.
80
Estadística Descriptiva
FRECUENCIAS
ACUMULADAS RELATIVAS
(%)
TEMPERATURAS LEÍDAS DURANTE UN MES EN UN
ARCHIVO
100
90
80
70
60
50
40
30
20
10
0
7.5
12.5
17.5
22.5
27.5
32.5
TEMPERATURAS
Comparemos los porcentajes y valores obtenidos en las dos ojivas:
ESTIMACIÓN
% de datos
menores de 20
grados
valores menores de
20 grados
% de datos mayores
de 25 grados
valores mayores de
25 grados
OJIVA CON
MARCAS DE CLASE
70%
OJIVA CON LÍMITES
REALES SUP.
60%
PORCENTAJE
REAL
56.6%
21
18
17
8%
20%
16.6%
2.4
6
5
En esta tabla se nota claramente que las estimaciones con la ojiva que
utiliza límites reales superiores en el eje de las “X” se acerca más a la realidad
que la ojiva con marcas de clase, esta es la razón de que a partir de este
momento, cuando se trate de trazar una ojiva porcentual se considerará en el
eje de las “X” a los límites reales superiores y en el eje de las “Y” las frecuencias
relativas acumuladas o frecuencias acumuladas relativas.
En la ojiva porcentual con límites reales superiores, también se puede
estimar el porcentaje de datos que caen entre dos valores dados, por ejemplo
entre 10 y 25:
81
FRECUENCIAS
ACUMULADAS RELATIVAS
(%)
TEMPERATURAS LEÍDAS DURANTE UN MES EN UN
ARCHIVO
100
90
80
70
60
50
40
30
20
10
0
7.5
12.5
17.5
22.5
27.5
32.5
TEMPERATURAS
El porcentaje de datos que se desea estimar caen entre estos dos
valores, de tal forma que a 10 le corresponde el 30% y a 25 el 80%, por lo
que una aproximación estará dada por 80%-30%=50%, lo cual nos dice que
15 datos caen en este rango, para verificar si esto es verdadero contemos
los datos utilizando la lista ordenada: 12, 12, 15, 15, 15, 18, 18, 18, 18, 21,
21, 21, 24, 24, 24 que son exactamente 15 temperaturas.
Además de las estimaciones anteriores, existen otros términos que se
usan para localizar puntos específicos en una distribución, tal es el caso de los
CUARTILES.
Los cuartiles son tres valores representados por Q1, Q2 y Q3 que dividen
a la población en cuatro partes iguales, cada uno de ellos contiene el 25% del
total de los datos considerados, denominándose respectivamente primer cuartil
=Q1, segundo cuartil =Q2 y tercer cuartil=Q3.
Si se considera una lista ordenada de todas las observaciones, es fácil
observar los puntos que representarían gráficamente a los cuartiles.
25%
—
primer dato
25%
—
Q1
25%
25%
—
Q2
50%
25%
—
Q3
75%
—
último dato
Ubiquemos en la ojiva porcentual el valor que le corresponde a cada uno
de los cuartiles:
82
Estadística Descriptiva
FRECUENCIAS ACUMULADAS RELATIVAS (%)
TEMPERATURAS LEÍDAS DURANTE UN MES EN UN ARCHIVO
100
95
90
85
80
75
70
65
60
55
50
45
40
35
30
25
20
15
10
5
0
7.5
12.5
17.5
22.5
27.5
32.5
TEMPERATURAS
aproximadamente
Q1=8.5
Q2=18.5
Q3=23.5
El segundo cuartil Q2 divide al total de las observaciones en dos partes
iguales de tal manera que a su izquierda se encuentra el 50% y a su
derecha el otro 50%.
En la siguiente unidad se te mostrará el procedimiento a seguir
para calcular los cuartiles en una distribución.
¿QUÉ HE APRENDIDO?
Antes de elaborar una gráfica es indispensable reflexionar sobre el tipo
de variable de que se trata a fin de que su representación sea lo más
ilustrativa posible del comportamiento de los datos considerados, por esta
razón te pido que en cada inciso indiques el tipo de variable (cualitativa o
cuantitativa) y la gráfica que utilizarías:
1) El número de libros por asignatura que tienes en tu biblioteca
personal.
83
variable__________________________________________________
_______
gráfica___________________________________________________
_______
2) El número de libros por asignatura que existen en la biblioteca más
importante de tu comunidad.
variable__________________________________________________
_______
gráfica___________________________________________________
_______
3) El número de nacimientos de tu localidad considerando intervalos de
5 años durante el período 1970-1995.
variable__________________________________________________
_______
gráfica___________________________________________________
_______
84
Estadística Descriptiva
Elabora el Resumen de la Unidad 3 ANOTANDO en cada descripción
la gráfica de que se trata y completando las características que encuentres
en blanco, al final de la guía lo encontrarás resuelto, de ser posible,
confronta tus respuestas y corrígelas en caso de ser erróneas.
TIPOS DE GRÁFICAS
_______________________________________
Características:
a)Es una circunferencia en el primer cuadrante del plano
cartesiano donde a la frecuencia de cada categoría le
corresponde un __________
b) Representación gráfica de ____________________
____________________________________________
c) El número de categorías a considerar debe ser menor
que en el de barras
________________________________________
Características:
a) Son barras unidas que se trazan en el primer cuadrante
del plano cartesiano
b) Representación gráfica de____________________
____________________________________________
c) En el eje de las “X” se marcan los puntos medios de
cada intervalo
d) En el eje de las “Y” se consideran las ___________
____________________________________________
________________________________________
Características:
a) Gráfica lineal trazada en el primer cuadrante del plano
cartesiano que tiene forma de “S”
b) Representación gráfica de ____________________
____________________________________________
c) En el eje de las “X” se marcan los ______________
____________________________________________
d) En el eje de las “Y” se marcan las frecuencias
acumuladas correspondientes a cada intervalo
e) Permite hacer estimaciones del comportamiento de los
datos considerando uno en particular
________________________________________
Características:
a) Son barras del mismo ancho trazadas en el primer
cuadrante del plano cartesiano
b) Las barras deben estar separadas _______________
____________________________________________
c) Representación gráfica de _____________________
____________________________________________
d) Considera pocas categorías
VARIABLES
CONSIDERADAS
a) Nominal
b) Ordinal
VARIABLES
CONSIDERADAS
a) Continuas
b) Discretas
VARIABLES
CONSIDERADAS
a) Continuas
b) Discretas
VARIABLES
CONSIDERADAS
a) Nominal
b) Ordinal
Continúa Resumen de la Unidad 3:
85
TIPOS DE GRÁFICAS
______________________________________
Características:
a) Gráfica lineal trazada en el primer cuadrante del plano
cartesiano que une los puntos medios de cada clase a la
altura de su frecuencia correspondiente
b) Representación gráfica de _________________
________________________________________
c) En el eje de las “X” se marcan los puntos medios de
cada intervalo, agregándose uno al inicio y otro al final de
los que se están considerando
d) En el eje de las “Y” las frecuencias correspondientes a
cada intervalo, agregándose _____________________
____________________________________________
____________________________________________
VARIABLES
CONSIDERADAS
a) Continuas
b) Discretas
NOTA: Es recomendable que todas las gráficas tengan un título que describa brevemente la
información que está siendo representada, así como la fuente de información, ya que éstas deben
ser autoexplicativas; con excepción de la gráfica de sectores, todas deben contener un título en
cada uno de los ejes que indique el tipo de datos que se están representando.
86
Estadística Descriptiva
EVALUACIÓN
1) Con los datos de la tabla de distribución para datos agrupados que
se elaboró en la Unidad 2 en el tema Distribución de Frecuencias
Agrupadas, realiza lo que se te pide en cada inciso:
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS DE DATOS POR INTERVALOS
NÚMERO DE LIBROS O EXPEDIENTES PRESTADOS
DURANTE 50 DÍAS
PERÍODO ENERO-MARZO 1997
CLASES
f
Mc
fa
fr
far
43- 47
4
45
4
8
8
48- 52
4
50
8
8
16
53- 57
11
55
19
22
38
58- 62
13
60
32
26
64
63- 67
10
65
42
20
84
68- 72
5
70
47
10
94
73- 77
3
75
50
6
100
TOTAL:
50
100
Fuente: Información proporcionada por el Departamento de Control Escolar.
a) Elabora histograma, polígono de frecuencias y ojiva porcentual en
papel milimétrico (una hoja por cada gráfica).
b)
La
forma
del
_______________________________________
c)
El
polígono
de
_________________________
frecuencias
histograma
presenta
un
es
sesgo
De acuerdo a la información contenida en la ojiva porcentual estimar:
d) El porcentaje de días en que se prestaron menos de 50 libros o
expedientes
________________________________________________________
_______
e)El porcentaje de días en que se prestaron más de 70 libros
________________________________________________________
_______
87
f) A los 25 días del período considerado se prestaron de ______ a
______ expedientes.
g) El porcentaje de días en que se prestaron de 63 a 68 expedientes.
________________________________________________________
_______
Verifica tus respuestas con la lista ordenada del número de libros o
expedientes prestados durante 50 días.
2) El Jefe de un Archivo (o Biblioteca que sólo atiende de lunes a
viernes), quiere conocer cómo se comporta la entrada de usuarios durante
el turno matutino, a fin de realizar una mejor distribución de tareas entre su
personal, para ello elige a una persona a quien le solicita obtenga la
información correspondiente.
El encargado de realizar la investigación recopila los datos
considerando una muestra de dos meses elegidos arbitrariamente y le
presenta a su jefe el siguiente gráfico:
% DE DÍAS CONSIDERADOS
AFLUENCIA DE USUARIOS DURANTE 61
DÍAS
100
90
80
70
60
50
40
30
20
10
0
19.5
25.5
31.5
37.5
43.5
49.5
55.5
61.5
NÚMERO DE USUARIOS
Ayuda al Jefe de Archivo (o Biblioteca) a contestar las siguientes
preguntas:
a) Si la persona que atiende al público en la mañana se queja de que
sólo puede atender satisfactoriamente un máximo de 52 usuarios y quiere
que se asigne otra persona que la auxilie en su labor ¿qué porcentaje de
días
se
atiende
a
un
número
mayor
de
personas?___________________________________________________
88
Estadística Descriptiva
b) Lo anterior indica entonces que ________ días atiende a menos de
52 usuarios.
c) La solución al problema de atención al público que tu darías es:
________________________________________________________
____________________________________________________________
______________
d) Obtener gráficamente Q2 que tiene un valor de
________________________, significa que la mitad de los 61 días (30
aproximadamente) se atienden entre ________ y __________ usuarios.
INSTRUCCIÓN GENERAL
De los siguientes ejercicios, resuelve el que corresponda a tu área, en
caso de que así lo desees, puedes resolver ambos.
3) Acude a una Biblioteca de tu localidad y durante 3 horas observa la
afluencia de usuarios a la misma y anota:
Tipo
de
biblioteca________________________________________________
Número
de
usuarios
biblioteca_________________________
Número
de
usuarios
servicio_____________________________
que
entran
por
a
área
la
de
Con la información obtenida realiza lo que se te pide en cada inciso:
a) Elabora una tabla de distribución de frecuencias simple con todos
sus datos (título, período, etc.)
89
b) Traza la gráfica que consideres más conveniente en papel
milimétrico y escribe cuál fue el motivo de tu decisión.
c)
¿Qué
servicio
tuvo
usuarios?_______________________
mayor
número
de
d) Calcula la proporción del servicio con mayor número de usuarios
con respecto al total de personas que entraron a solicitar un servicio durante
el
tiempo
de
la
investigación.__________________________________________________
___
e) Estima un porcentaje con los datos de la gráfica y verifica tu
respuesta
con
la
información
obtenida
en
tu
investigación.___________________________________
f) Marca en la gráfica con color rojo los cuartiles.
4) Con la información que obtuviste al acudir a un Archivo de Trámite
(Oficina de Gobierno Administrativa, Archivo Estatal, Municipal o de la
Localidad) en la Evaluación de la UNIDAD I, realiza lo que se te pide en
cada inciso:
a) Elabora una tabla de distribución de frecuencia simple con todos sus
datos que muestre el comportamiento de la entrada de documentación
durante 30 días tomados arbitrariamente.
b) Traza la gráfica que consideres más adecuada en papel milimétrico
y explica el motivo de tu decisión.
90
Estadística Descriptiva
c) Estima un porcentaje a través de la gráfica y verifica tu respuesta
con la información obtenida inicialmente.
d) Calcula el número aproximado de documentos que se atienden
mensualmente.
e) Marca en la gráfica con color rojo los cuartiles.
ENVÍA A TU ASESOR
Ahora sólo te falta una unidad para terminar. ¡Bien hecho!
91
EDADES
16
17
18
f
2
1
3
UNIDAD 4
ESTADÍSTICA
DESCRIPTIVA
En esta unidad analizaremos la información que aparece en las
diferentes tablas de distribución. Primeramente conoceremos los valores de
la variable que señalan un valor central alrededor del que se agrupa el
mayor número de los datos obtenidos y que indican el comportamiento de la
población; estos valores se encuentran incluidos en el tema de Medidas de
Tendencia Central.
Posteriormente, calcularemos las Medidas de
Dispersión, las cuales describen la forma en que se distribuyen los datos,
para finalmente terminar con el Teorema de Chebyshev que permite medir
las variaciones de los datos con respecto a la media.
¿QUÉ VOY A APRENDER EN ESTA UNIDAD?
A calcular Medidas de Tendencia Central (Media, Moda y Mediana)
que muestran los valores centrales de una distribución y Medidas de
dispersión (Rango, Desviación Media, Varianza, Desviación Estándar,
Coeficiente de variación y Cuartiles) que también reciben el nombre de
medidas de variabilidad porque permiten calcular el valor de la dispersión
92
Estadística Descriptiva
de los datos, finalmente a través del Teorema de Chebyshev se manejará y
entenderá el concepto de desviación típica.
93
DIAGNÓSTICO
1) Pregúntales a 10 de tus amigos su edad y anótala, incluye la tuya.
________________________________________________________
_______
2) Las edades que obtuviste ordénalas en forma ascendente.
________________________________________________________
_______
3) Observa y escribe la edad que se localiza en el centro de la lista
ordenada.____________________________________________________
________
4)
Calcula
y
anota
_________________________________
5)
Escribe
la
edad
____________________________
que
la
se
edad
repite
promedio.
más
veces.
6) ¿Cómo son los valores que obtuviste en los incisos 3, 4 y 5, están
próximos
o
alejados?
__________________________________________________________
Es de gran utilidad que recuerdes tu experiencia previa sobre el cálculo
de promedios, ya que sólo se trata de sumar todos los valores considerados
y el resultado dividirlo entre el número de datos.
También es importante que a lo largo de esta unidad observes
cuidadosamente los valores que vas obteniendo, esto te permitirá más
adelante inferir y llegar a conclusiones válidas y verdaderas que reflejen no
sólo el cuidado de tus cálculos sino la lógica de ver más allá de lo que tu
ojos pueden observar.
94
Estadística Descriptiva
95
4.1 MEDIDAS DE TENDENCIA CENTRAL
?
4.1.1 MEDIA
4.1.2 MEDIANA
4.1.3 MODA
Como se mencionó al principio de esta unidad, las medidas de
Tendencia Central son valores representativos de la población que nos
indican los valores centrales alrededor de los cuales se agrupa el total de
datos y son MEDIA, MODA y MEDIANA.
El cálculo de estas medidas depende de los datos que se están
considerando y que pueden ser:
1) DATOS NO AGRUPADOS
a) Si se trata de una lista de números como: 18, 17, 19, 16, 20
b) Datos en una tabla de distribución de frecuencias simple (en donde
no aparecen intervalos):
EDADES
16
17
18
f
2
1
3
2) DATOS AGRUPADOS
a) Si estos se encuentran en una tabla de distribución de frecuencias
(con intervalos):
CLASES
18 - 20
21 - 23
24 - 26
f
5
6
3
Antes de definir cada una de las Medidas de Tendencia Central,
introduciremos la notación matemática que se utiliza para abreviar sumas,
denominada “notación Sigma” debido a que usa la letra griega sigma (Σ).
96
Estadística Descriptiva
n
Σ xi
i=1
x representa el valor del dato a considerar, el cual inicia con i=1 hasta
el enésimo (n).
Para comprender mejor esta notación, consideremos algunos datos del
mismo tipo:
2
x1
5
x2
4
x3
6
x4
9
x5
A los números se les ha colocado una etiqueta, la letra “x”, con un
subíndice para saber de cuántos números se trata. Se hace hincapié en que
los datos no necesariamente tienen que estar ordenados.
La notación sigma es de gran utilidad ya que para indicar la suma de
estos 5 números se escribe:
n
Σ xi
i=1
En este caso el primer subíndice es 1, lo cual se expresa con i=1 y el
último es 5, por ello n=5 y se lee “La suma de las xi donde i (el subíndice)
inicia con 1 y termina en 5”, esta es la forma abreviada de indicar la suma
de los cinco números anteriores.
Al substituir se tiene:
5
Σ xi = x1 +x2 + x3 + x4 + x5 = 2 + 5+ 4+ 6+ 9 = 26
i=1
1) Considerando la siguiente serie contesta lo que se te pide en los
incisos:
4
x1
2
x2
7
x3
6
x4
10
x5
3
a) Σ xi = x1 +x2 + x3 =
i=1
97
5
b) Σ xi = x2 +x3 + x4 + x5 =
i=2
5
c) Σ xi = x1 +x2 + x3 + x4 + x5 =
i=1
MEDIDAS DE TENDENCIA CENTRAL PARA DATOS NO
AGRUPADOS:
_
MEDIA ARITMÉTICA (X)
Esta Medida de Tendencia Central es la que se utiliza con mayor
frecuencia, tú ya la has manejado, se conoce también con los nombres de
Valor medio, Promedio Aritmético, Media Aritmética o simplemente Media y
es la suma de los datos o puntuaciones consideradas, dividida entre el
número de casos.
Más formalmente se dice que la Media de un conjunto de datos x1, x2,
x3, ... xn, es igual a la suma de los valores de las x´s divida entre el tamaño
de la muestra (n) o población (N); esto queda representado en la siguiente
fórmula:
MUESTRA tamaño n:
n
Σ xi
_ i=1
ΣX
MEDIA= X = ------------- = ------------------------n
n
_
X se lee “equis” barra.
POBLACIÓN tamaño N:
n
Σ xi
i=1
ΣX
MEDIA= µ = ------------- = ------------------------N
N
µ es la letra griega “mu”
2) Obtener la media de las calificaciones que un alumno obtuvo
durante un semestre en la Asignatura de Métodos Estadísticos : 8, 7, 6 y 10.
98
Estadística Descriptiva
_
ΣX
8 + 7 + 6 + 10
31
X= -------------------- = ----------------------- = -------- = 7.75
n
4
4
Redondeando al entero más próximo se tiene que la calificación
promedio que este alumno logró en el semestre es de 8.
MODA (Mo)
En un conjunto de datos la moda es el valor que se repite más veces o
que tiene mayor frecuencia. Para encontrar esta medida cuando se tienen
datos no agrupados, primero se ordenan los datos en forma ascendente.
3) A un grupo de 20 alumnos se les preguntó su promedio del
semestre, los valores proporcionados fueron:
8, 7, 9, 9, 10, 10, 8, 6, 7, 7, 8, 9, 9, 8, 8, 9, 10, 7, 9, 10.
Calcular media y moda.
La media es:
_
ΣX
8+7+9+9+10+10+8+6+7+7+8+9+9+8+8+9+10+7+9+10
168
X= -------------------- = ---------------------------------------------------------------------- =------------ =8.4
n
20
20
_
X= 8
Para encontrar la moda, primero se ordenan los datos en forma
ascendente:
6, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10.
El valor de mayor frecuencia es 9, entonces Mo=9 y es unimodal.
Nota: Toda distribución que tiene una sola moda recibe el nombre de unimodal, si tiene 2
bimodal y si tiene más de 2 multimodal.
MEDIANA (Md)
Dado un conjunto de valores ordenados en forma ascendente, la
mediana es el valor que se encuentra a la mitad de la serie, arriba de ella
99
está el 50% del total de datos y abajo el 50% restante. Dependiendo del
número de datos, se consideran dos casos:
a)En una serie formada por un número impar de datos la mediana
ocupa el lugar (n+1)/2.
Si los valores ordenados son:
1, 2, 2, 3, 3, 5, 7, 8, 8,
el valor de la mediana ocupa el lugar (9+1)/2 = 5, lo cual indica que es
el valor del quinto lugar que en este caso es el número 3.
b) Si n es par la mediana es el promedio de los valores centrales.
Tomemos los siguientes datos: 23, 27, 36, 38, 40, 51
La mediana es igual al promedio del valor que ocupa el lugar n/2 y del
que ocupa el lugar n/2 + 1
n/2 = 6/2 = 3 este lugar es ocupado por el 36.
n/2 + 1 = 6/2 + 1 = 4 aquí se encuentra el 38.
Calculando el promedio de 36 y 38 tenemos que:
36 + 38
Md= ------------ = 37
2
Para encontrar la mediana de los promedios de los alumnos
considerados en el inciso 3) se debe trabajar nuevamente con la lista
ordenada en forma ascendente. Como se tiene un número par de datos, la
mediana es el promedio del valor central:
6, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 10, 10, 10, 10
La mediana es (8+9)/2 )= 8.5
Agrupemos en una tabla de distribución de frecuencia simple los
promedios de los 20 alumnos y calculemos su media con la fórmula:
n
Σfx
i=1
X= -------------------n
100
Estadística Descriptiva
fx es el producto de cada valor (x) por su frecuencia (f).
PROMEDIO
x
6
7
8
9
10
FRECUENCIA
f
1
4
5
6
4
20
Observemos que la suma de la columna de frecuencias es el valor de n
(20).
Para encontrar la media se obtiene la suma de todos los datos, para ello se
multiplica en cada renglón el valor de equis “x” por el número de veces que se
repite, esto es, por su frecuencia. Los resultados se escriben en la columna
correspondiente:
PROMEDIO
x
FRECUENCIA
f
6
7
8
9
10
1
4
5
6
4
20
PROMEDIO
MULTIPLICADO POR
FRECUENCIA (fx)
6
28
40
54
40
168
En este caso 168 es la sumatoria de las frecuencias multiplicadas por
x, esto es igual a Σfx
Al sustituir los valores correspondientes:
_
Σfx
168
X= -------------------- = ----------- = 8.4 que redondeando es 8.
n
20
La moda (Mo) es la categoría con mayor frecuencia, que en este caso
es 9, ya que tiene frecuencia 6.
A fin de encontrar la mediana se calcula la columna de frecuencias
acumuladas (fa).
PROMEDIO
x
6
7
FRECUENCIA
f
1
4
fa
1
5
101
8
9
10
5
6
4
20
10
16
20
y se realizan los siguientes pasos:
1) Calcular el cociente n/2 = 20/2 = 10
2) Ubicar en qué renglón de fa cae el número n/2=10
3) La categoría que contiene a n/2 es el valor de la mediana
PROMEDIO
x
6
7
8
9
10
FRECUENCIA
f
1
4
5
6
4
20
fa
1
5
10
16
20
n/2= 10 cae aquí
Entonces Md = 8
Como te habrás dado cuenta, tanto la media como la moda aunque
fueron calculadas por diferentes procedimientos se obtuvieron los mismos
resultados; sin embargo, la mediana tuvo una mínima diferencia de .5.
En ocasiones se presentan series que no tienen moda como: 1, 3, 5, 7,
8, 12, aunque si media (6) y mediana (7).
CARACTERÍSTICAS
TENDENCIA CENTRAL:
IMPORTANTES
DE
LAS
MEDIDAS
DE
La media tiene la desventaja de ser sensible a valores extremos,
esto significa que si dentro de una serie de números se considera un valor
“distinto” a los demás, la media varía considerablemente.
La moda no es sensible a valores extremos, pero tiene el
inconveniente de no ser única y en algunos casos ésta difiere en muy poco
de otros valores del conjunto o es un valor extremo. Al obtener la moda de
un conjunto de datos, es necesario expresar claramente si es unimodal por
tener una moda, bimodal por tener dos o si tiene una moda principal y una
secundaria en caso de que la diferencia entre ambos valores sea mínima.
102
Estadística Descriptiva
La medida de tendencia central que se recomienda para ser utilizada
en el análisis de datos es la mediana, por su virtud de no ser sensible a
valores extremos y además, ser única.
Consideremos el conjunto formado por: 3, 6, 7, 8, 10 y calculemos
sus medidas de tendencia central:
MEDIA:
_
3+6+7+8+10
34
La media es igual a X = ------------------------------- = ------------- = 6.8 aproximadamente 7.
5
5
MODA: No tiene
MEDIANA: es 7.
Si en lugar del número 10 tomamos al 40 (que es un valor diferente a
los demás), tendremos: 3, 6, 7, 8, 40
MEDIA:
_
3+6+7+8+40
64
La media es igual a X = ------------------------------- = ------------- = 12.8 aproximadamente 13.
5
5
MODA: No tiene
MEDIANA: sigue siendo el número 7.
Si comparamos los resultados obtenidos en la serie 3, 6, 7, 8,10 con
los que se obtienen al sustituir el 10 por 40, la media ha cambiado, mientras
que la mediana sigue siendo la misma.
En el siguiente ejemplo calcularemos las Medidas de Tendencia
Central:
El personal de un Archivo está integrado por 110 personas, de las
cuales 70 son de base con un sueldo mensual de $1,800.00 y el resto
están contratadas por honorarios con un sueldo mensual de $3,000.00, en
una junta se solicita al Director del mismo un aumento salarial y éste les
informa que no es posible ya que el salario promedio de los empleados es
de $2,236.00 y rebasa al que actualmente se paga en otros archivos.
Calculemos las medidas de tendencia central:
103
SUELDO
MENSUAL
x
1,800.00
3,000.00
FRECUENCIA
f
70
40
110
SUELDO
MULTIPLICADO POR
FRECUENCIA (fx)
126000
120000
246000
_
246000
X = --------------- = 2236.36
110
La categoría de mayor frecuencia
$1,8000.00
pertenece a la Moda: Mo =
En este ejercicio, escribir 70 veces $1,800.00 y 40 veces $3,000.00
para conocer el valor central resulta bastante tedioso, así que primero
averiguaremos en qué categoría “cae” el valor central, recordando que la
columna de frecuencias acumuladas (fa) nos permite conocer la ubicación
del dato que buscamos:
SUELDO
MENSUAL
x
1,800.00
3,000.00
FRECUENCIA
f
70
40
110
SUELDO
MULTIPLICADO POR
FRECUENCIA (fx)
126000
120000
246000
FRECUENCIA
ACUMULADA
fa
70
110
Como n es par (n=110), calculemos el lugar que ocupan los valores
centrales:
n/2= 55
n/2 + 1 = 56
Ambos valores caen en la primera categoría ya que ésta contiene a los
valores que ocupan el primer lugar hasta el septuagésimo, por lo que la
Mediana es $1,800.00
104
Estadística Descriptiva
¿QUÉ HE APRENDIDO?
1) En este último ejemplo ¿consideras que el Director del Archivo ha
optado por la mejor medida de tendencia central para no permitir el
aumento de sueldo?
________________________________________________________
____________________________________________________________
______________
2) ¿Qué argumento darías para convencer al Director del Archivo, a fin
de que modifique su opinión acerca de considerar el salario promedio como
un parámetro confiable?
________________________________________________________
____________________________________________________________
_______________
3) Escribe tu propia definición de cada una de las Medidas de
Tendencia Central.
________________________________________________________
____________________________________________________________
_______________
MEDIDAS DE TENDENCIA CENTRAL PARA DATOS AGRUPADOS:
Como ya se dijo al inicio de esta unidad, los datos agrupados se
encuentran en una tabla de distribución de frecuencias en donde el
representante de cada intervalo es la Marca de clase también denominada
punto medio, esta es la razón por la cual para encontrar la media, se
multiplica la marca de clase de cada intervalo por su frecuencia respectiva
(indica el número de datos del intervalo), se suman los resultados obtenidos
y se divide entre la suma de frecuencias. La fórmula que representa las
operaciones ya descritas es:
n
∑Mcf
∑f(Mc)
_
i=1
MEDIA= X = --------------= --------------n
n
105
Considerando a n como el tamaño de la muestra.
A fin de establecer el procedimiento para el cálculo de las Medidas de
Tendencia Central para datos que se encuentran incluidos en intervalos,
realicemos el siguiente ejercicio.
Se pretende conocer la asistencia promedio de usuarios a una
biblioteca que atiende al público durante todos los días del año, en el receso
julio-agosto, para ello se considera el número de usuarios que acudieron en
la misma fecha el año pasado, obteniéndose la siguiente tabla de
distribución de frecuencias para datos agrupados:
CLASES
(USUARIOS)
X
20-24
25-29
30-34
35-39
40-44
45-49
NÚMERO DE
DÍAS
f
12
9
19
8
7
6
61
Es necesario encontrar la marca de clase de cada intervalo y
multiplicarla por su frecuencia respectiva (columna fMc):
CLASES
20 24
25 29
30 34
35 39
40 44
45 49
f
12
9
19
8
7
6
61
Mc
22
27
32
37
42
47
fMc
264
243
608
296
294
282
1987
Se sustituye ∑fMc= 1987 y n=61 en la fórmula para obtener la media:
_
∑Mcf
∑f(Mc)
1987
_
MEDIA= X = --------------= --------------- = ----------- =32.5 redondeando X= 33
n
n
61
La asistencia promedio de usuarios a la biblioteca durante el periodo
julio-agosto fue de 33 personas.
106
Estadística Descriptiva
Esta medida de tendencia central que acabamos de calcular recibe el
nombre de MEDIA PONDERADA, ya que se obtuvo al multiplicar cada
representante (Mc) por su “peso” que en este caso es su frecuencia (f)
correspondiente y el resultado se dividió entre la suma de todos los “pesos”
o frecuencias.
Para encontrar la moda se debe aplicar la fórmula:
d1
MODA = Mo = Li + ( -------------- ) A
d1 + d2
Para algunos autores Li es el límite inferior y para otros el límite real
inferior, cualquiera de las dos alternativas es válida, ya que si recordamos,
la diferencia entre ambos límites es .5.
En el cálculo de esta medida nosotros definimos a Li = límite inferior
del intervalo de la clase de mayor frecuencia o clase modal.
d1 = frecuencia de la clase modal menos la frecuencia de la clase
anterior.
d2= frecuencia de la clase modal menos la frecuencia de la clase
posterior a la clase de la moda.
A = amplitud de cualquiera de los intervalos de la tabla (todos tienen la
misma amplitud) es la diferencia entre cualesquiera 2 fronteras o límites
inferiores.
Observemos las frecuencias de los intervalos y destaquemos el mayor.
CLASES
(USUARIOS)
X
20-24
25-29
30-34
35-39
40-44
45-49
NÚMERO DE
DÍAS
f
12
9
19
8
7
6
61
intervalo de mayor frecuencia o clase
modal
Li =30
d1 = 19 - 9 = 10
d2 = 19 - 8 = 11
A = 25-20 = 5
Los valores obtenidos se sustituyen en la fórmula:
d1
107
Mo = Li + ( -------------- ) A
d1 + d2
10
50
Mo = 30 + ( ----------- ) 5 = 30 + ----- = 30 + 2.3 = 32.3 redondeando Mo = 32
10 + 11
21
La mediana (Md) de un conjunto de datos en una tabla de distribución
para datos agrupados, se calcula con:
n/2 - F
MEDIANA = Md = Li + ( -------------- ) A
f
donde:
Li = límite inferior del intervalo que contiene a la mediana o clase de la
mediana.
n/2 = es el tamaño de la muestra dividido entre dos.
F = frecuencia acumulada (fa) de la clase anterior a la clase de la
mediana.
f= frecuencia absoluta (f) del intervalo que contiene a la mediana.
A = amplitud de la clase de la mediana.
Iniciamos agregando a la tabla de frecuencias la columna de
frecuencias acumuladas:
CLASES
20
24
25
29
30
34
35
39
40
44
45
49
f
12
9
19
8
7
6
61
Li = 30
n/2 = 30.5
F = 21
f = 19
108
Mc
22
27
32
37
42
47
fMc
264
243
608
296
294
282
1987
fa
12
21
40
48
55
61
Para encontrar la clase de la mediana
calculamos n/2 = 61/2 = 30.5 y vemos
dónde “cae” este valor en fa.
en este intervalo cae 30.5
por lo que 30-34 es la clase de la
mediana.
Estadística Descriptiva
A= 5
Al sustituir estos valores en la fórmula tenemos:
n/2 - F
30.5 - 21
47.5
Md = Li + ( -------------- ) A = 30 + ( --------------) 5 = 30 + ------- = 30 + 2.5 redondeando Md =33
f
19
19
Podemos concluir que durante el período julio - agosto:
_
X = 33
El promedio de usuarios fue de 33 personas.
Mo = 32
Durante 19 días asistieron 32 usuarios a la biblioteca, estos fueron los
días de mayor asistencia.
Md = 33
Este es el número de usuarios que asistieron a la biblioteca y que tiene
tanto a su derecha como a su izquierda la mitad de las frecuencias.
Para concluir este tema y analizar las medidas de tendencia central,
veamos el siguiente ejemplo en donde se ha tomado el número de
expedientes que solicitan en un mes los investigadores que acuden a un
Archivo:
NÚMERO DE
NÚMERO DE
EXPEDIENTE INVESTIGADOR
S
ES
(x)
(f)
1
3
50
4
6
35
7
9
22
10
12
36
13
15
21
16
18
9
19
21
7
180
Mc
fMc
fa
2
5
8
11
14
17
20
100
175
176
396
294
153
140
1434
50
85
107
143
164
173
180
1434
X = ---------- = 7.9 ≅ 8 expedientes
180
Conclusión: En promedio los investigadores solicitan mensualmente
un promedio de 8 expedientes.
109
Para la moda encontramos los valores necesarios y los sustituimos en
la expresión correspondiente:
clase modal 1- 3
Li =1
d1 = 50-0 = 50 (la frecuencia anterior a la clase modal es 0)
d2 = 50- 35 = 15
A = 4-1 = 3
d1
Mo = Li + ( -------------- ) A
d1 + d2
50
150
Mo = 1 + ( ----------- ) 3 = 1 + ----- = 1 + 2.3 = 3.3 ≅ 3 expedientes
50 + 15
65
Conclusión: El número de investigadores que solicitan 3 expedientes
es el más numeroso, ya que le corresponde un total del 27.7% que es el
porcentaje de la clase modal.
A fin de ubicar la clase de la mediana primero calculamos n/2 = 90 al
observar la columna de fa podemos decir que se trata del intervalo 7-9 por
lo que:
Li =7
F =85
f =22
A=3
n/2 - F
MEDIANA = Md = Li + ( -------------- ) A
f
90-85
15
Md = 7 + ( -------------- ) 3 = 7 + ------- = 7 + .68 = 7.68 ≅ 8
22
22
Si se tuviera el listado de todos los datos ordenados en forma
ascendente, tendríamos que el valor central es 8, esto quiere decir que el
50% del total de investigadores (90) solicitan en un mes de 1 a 8
expedientes, es decir, como máximo 8 expedientes.
110
Estadística Descriptiva
¿ QUÉ HE APRENDIDO?
LECTURA 3
A fin de reforzar los conocimientos que acabas de adquirir sobre las
medidas de tendencia central, es necesario que leas el libro Estadística
Paso a Paso de Howard B. Christensen de la página 102 a la 111, incluido
al final de esta guía, revises los ejemplos y verifiques el resultado por lo
menos en 3 de ellos; después de leer elabora el resumen correspondiente y
resuelve los ejercicios que se te solicitan enseguida.
1) Explica por lo menos dos características de las siguientes
distribuciones:
a) Unimodal
b) Bimodal
2) Traza en papel milimétrico un polígono unimodal y simétrico de
frecuencias absolutas y localiza la media, la moda y la mediana.
3) Pregunta a 8 de tus amigos su ingreso mensual, ordénalo en forma
ascendente y encuentra las medidas de tendencia central indicando la
cantidad que es la más representativa de todas.
111
4.2 MEDIDAS DE DISPERSIÓN
X
4.2.1 RANGO
4.2.2 CUARTILES
Hasta aquí sólo se han considerado los valores centrales de una
distribución, esto no es suficiente para conocer el comportamiento de los
datos, razón que nos motiva a calcular otro tipo de medidas que nos
informen qué tan próximos o alejados están de la media (X), por lo que
ahora nos ocuparemos de las medidas de dispersión que nos permiten
evaluar la variabilidad y dispersión de los datos en una distribución, siendo
las más conocidas: RANGO, DESVIACIÓN MEDIA, VARIANZA y
DESVIACIÓN ESTÁNDAR.
RANGO O AMPLITUD total (también llamado extensión o recorrido)
sólo considera los valores extremos, por lo que debe tomarse únicamente
como un índice preliminar o muy aproximado, éste se calcula restando al
valor máximo alcanzado por la variable el valor mínimo. Esta medida se
obtuvo cuando se elaboró la tabla de distribución de frecuencias para datos
agrupados.
Rango = R = Valor máximo - Valor mínimo
Supongamos que en un examen de Estadística practicado a los grupos
A y B las calificaciones fueron:
GRUPO A 6
GRUPO
6
B
7
7
7
7
8
7
8
7
8
8
8
9
9
9
9
10
10
10
_
MEDIA DEL GRUPO A= X = 8
RANGO= R= 10 - 6 = 4
_
MEDIA DEL GRUPO B= X = 8
RANGO = R = 10 - 6 = 4
Ambos grupos tienen la misma media, lo que podría hacernos suponer
que no hay diferencias entre las calificaciones de ambos grupos, sin
112
Estadística Descriptiva
embargo, claramente se observa que sí existe variación, lo que tampoco es
reportado por el rango. Lo anterior indica que el rango no es una medición
precisa y sólo se debe utilizar como un valor aproximado.
RANGO INTERCUARTIL de un grupo de observaciones es la
diferencia entre los valores del primero y tercer cuartil y se simboliza con Q:
Q = Q3 - Q1
Antes de continuar, veamos la forma en que se calculan los cuartiles,
para posteriormente poder calcular el rango intercuartil.
CÁLCULO DE LOS CUARTILES
Anteriormente ya nos habíamos referido a los cuartiles como tres
valores denominados Q1, Q2 y Q3 que dividen al total de datos de una
distribución en tres partes iguales, aunque sólo los habíamos visualizado
en la ojiva porcentual, en este capítulo haremos los cálculos
correspondientes para obtenerlos no sin antes indicarte que también son
medidas de dispersión.
Para calcular los tres cuartiles ya mencionados se utilizan las fórmulas
que aparecen en seguida, ten cuidado en la sustitución de los datos.
En todos los casos A es la amplitud del intervalo respectivo (todos son
iguales):
n/4 - F1
Q1 = L1 + ( -------------- ) A
f1
L1 es el límite inferior del intervalo del primer cuartil.
f1 frecuencia absoluta del primer cuartil.
F1 frecuencia acumulada anterior al intervalo del primer cuartil.
n número total de datos.
2n/4 - F2
Q2 = L2 + ( -------------- ) A
f2
L2 es el límite inferior del intervalo del segundo cuartil.
f2 frecuencia absoluta del segundo cuartil.
F2 frecuencia acumulada anterior al intervalo del segundo cuartil.
n número total de datos.
113
3n/4 - F3
Q3 = L3 + ( -------------- ) A
f3
L3 es el límite inferior del intervalo del tercer cuartil.
f3 frecuencia absoluta del tercer cuartil.
F3 frecuencia acumulada anterior al intervalo del tercer cuartil.
n número total de datos.
Iniciemos el cálculo de los cuartiles en la tabla que hemos venido
trabajando:
CLASES
20
24
25
29
30
34
35
39
40
44
45
49
f
12
9
19
8
7
6
61
Mc
22
27
32
37
42
47
fMc
264
243
608
296
294
282
1987
fa
12
21
40
48
55
61
En el cálculo de cada uno de los cuartiles, el primer paso es encontrar
el intervalo del cuartil que ese está calculando, la clave está en efectuar las
operaciones que involucran al número total de datos que es n:
n/4 - F1
Q1 = L1 + ( -------------- ) A
f1
n/4 = 61/4 = 15.25 este valor al ser localizado en la columna de
frecuencias acumuladas (fa), nos indica el intervalo que estamos buscando,
en este caso es 25-29 de donde tenemos:
A= amplitud del intervalo = 5
L1 es el límite inferior del intervalo del primer cuartil = 25
f1 frecuencia absoluta del primer cuartil = 9
F1 frecuencia acumulada anterior al intervalo del primer cuartil = 12
Estos datos se sustituyen en la fórmula:
15.25 - 12
16.25
Q1 = 25 + ( -------------- ) 5 = 25 + ---------------= 25 + 1.8 = 26.8
9
9
114
Estadística Descriptiva
Por lo tanto Q1 = 26.8 ≅ 27 (el símbolo ≅ significa aproximadamente
igual a)
Al realizar el mismo procedimiento para el segundo cuartil tenemos que
2n/4 = 122/4 = 30.5 al localizarlo en fa obtenemos el intervalo del segundo
cuartil que es 30-34.
L2 = 30
f2 = 19
F2 = 21
Al ser sustituidos los valores encontrados en la fórmula que le
corresponde, observamos que son los mismos que dieron origen a la
mediana:
30.5 - 19
Q2 = 30 + ( -------------- ) 5 = 30 + 2.5 ≅ 33
21
Como resultado se tiene entonces que Q2 = mediana
distribución, ya que ambos la dividen en dos partes iguales.
de la
Realiza los cálculos necesarios para encontrar el valor del tercer
cuartil.
Intervalo del tercer cuartil =
L3=
f3 =
F3 =
Q3 =
Ya podemos calcular el rango intercuartil:
Q3 = 39
Q2 = 33
Q = 39 - 33 = 6
115
¿ QUÉ HE APRENDIDO?
1) Con la información de la siguiente tabla encuentra los cuartiles y
contesta lo que se te pide:
CLASES
4-10
10-16
16-22
22-28
28-34
TOTAL
f
5
15
30
10
6
66
a) Si Q1 = ___________ quiere decir que el 25% de los datos tiene
valores comprendidos entre ________ y ___________________.
b) Como Q2= _________ significa que el ________ de los datos se
encuentran entre 4 y ____________.
c) Dado que Q3= ___________ el ________ de los datos son valores
entre _________ y ____________.
116
Estadística Descriptiva
4.2.3 DESVIACIÓN MEDIA
CÁLCULO DE LA DESVIACIÓN MEDIA PARA DATOS NO
AGRUPADOS:
DESVIACIÓN MEDIA (DM) es el promedio de las desviaciones a partir
de un valor central (media, moda o mediana), lo más común es trabajar con
la Media.
A fin de ejemplificar el uso de esta medida tomemos nuevamente la
tabla de la página 127.
Para conocer la variabilidad de las calificaciones del grupo A con
respecto a la media se requiere encontrar la diferencia entre cada
calificación y la media, la cual recibe el nombre de desvío o desviación:
_
desvío o desviación = d = x - X
donde x es el dato y X la media de la distribución
_
A cada uno de los datos se le resta la media X= 8 para obtener el
desvío correspondiente:
GRUPO A
6
7
7
8
8
8
8
9
9
10
DESVÍO
6 -8
-2
7-8
-1
7-8
-1
8-8
0
8-8
0
8-8
0
8-8
0
9-8
1
9-8
1
10-8
2
El signo menos (-) está indicando que la dirección de los desvíos es
hacia la izquierda de la media.
Al sumar los desvíos se tiene: -2-1-1+1+1+2= 0, lo cual indica que la
suma de las desviaciones de las variables mayores que la media es igual y
de signo contrario a la suma de las desviaciones de las variables menores
que la media, esto significa que siempre que se consideran a los desvíos
con su signo correspondiente se llega a que la suma de todas es cero “0”, lo
cual no tiene sentido, es por ello que para calcular la cantidad de
variabilidad o distancia de las desviaciones, no se deben tomar en cuenta
las direcciones, es decir, los desvíos se suman considerándolos positivos,
lo que se conoce como valor absoluto y el resultado se divide entre el
tamaño de la población o muestra.
117
Debemos tener presente que dado cualquier número positivo o
negativo, su valor absoluto es el número que representa, por ejemplo:
El valor absoluto de 2 se escribe ⏐2 ⏐ = 2
absoluto
y el valor absoluto de -2 es
⏐-2⏐ = 2
en ambos casos las barras ⏐⏐ indican valor
Ahora veamos la forma en que se calcula la desviación media de datos
contenidos en una tabla de distribución simple, utilizando las mismas
calificaciones del grupo A:
El cálculo de la desviación media del grupo A considerando el valor
absoluto de los desvíos es:
2+1+1+1+1+2
8
DMA = ------------------------------ = ------ = .8
10
10
Esta medida de dispersión indica que la variabilidad promedio de todos
los valores de la distribución con respecto a la media es .8, en otras
palabras, que en promedio el grupo obtuvo una calificación de 8 con una
desviación promedio de .8 de más o de menos.
Una característica de las desviaciones absolutas es que su suma
tiende a agrandarse a medida que aumenta la dispersión o variabilidad de la
distribución.
La desviación media para datos no agrupados considerando una
muestra con tamaño n se calcula con la fórmula:
n
n
_
∑⏐x⏐
∑⏐xi - X⏐
i=1
i=1
DM = --------- = -------------n
n
Para una población de tamaño N la desviación media es:
n
n
∑⏐x⏐
∑⏐xi - µ⏐
i=1
i=1
DM = --------- = ----------------N
N
118
Estadística Descriptiva
Las diferencias xi - X
y xi - µ reciben el nombre de desvío o
desviación, como ya se dijo anteriormente, y ∑⏐x⏐= ∑⏐xi - X⏐ representa la
suma de las desviaciones absolutas, esto es, sin tomar en cuenta los signos
de los valores de la variable.
CALIFICACIONES OBTENIDAS POR EL GRUPO A
EN UN EXAMEN DE ESTADÍSTICA
CALIFICACIONES
NÚMERO DE
x
ALUMNOS
f
6
1
7
2
8
4
9
2
10
1
TOTAL
10
En una tabla de distribución de frecuencia simple la DM se encuentra
con la siguiente expresión:
_
∑f⏐xi - X⏐
_
DM = -------------------- en donde se puede sustituir ⏐d⏐=⏐xi - X⏐
n
_
Encontremos la DM en la siguiente tabla con X=8:
CALIFICACIONES
x
6
7
8
9
10
TOTAL
NÚMERO DE
ALUMNOS
f
1
2
4
2
1
10
_
xi - X
_
⏐xi - X⏐
_
f⏐xi - X⏐
-2
-1
0
1
2
2
1
0
1
2
2
2
0
2
2
8
este total es _
f ⏐xi - X⏐
∑f⏐xi - X⏐
8
DMA = -------------------- = ------- = .8
n
10
Como te habrás dado cuenta, el resultado obtenido para el grupo A en
la lista de calificaciones y en la tabla de distribución de frecuencia simple es
el mismo.
Como DMA = .8 podemos asegurar que la dispersión de los valores es
relativamente pequeña.
119
¿ QUÉ HE APRENDIDO?
Para reforzar tu aprendizaje resuelve lo que se te solicita considerando
los datos del Grupo B:
GRUPO
B
6
7
7
7
7
8
9
9
10
10
1) Calcula la desviación media para datos en forma de lista.
DMB=
CALIFICACIONES
x
NÚMERO DE
ALUMNOS
f
_
xi - X
_
⏐xi - X⏐
_
f⏐xi - X⏐
6
7
8
9
10
TOTAL
DMB=
3) Verifica que los resultados obtenidos en los dos incisos anteriores
sean los mismos.
4) ¿Cuál de los dos grupos (A o B) presenta mayor desviación media y
por lo tanto tiene mayor dispersión o variabilidad en sus calificaciones?
____________________________________________________________
________
120
Estadística Descriptiva
CÁLCULO
AGRUPADOS
DE
LA
DESVIACIÓN
MEDIA
PARA
DATOS
Con el propósito de encontrar la desviación media en una tabla de
distribución de frecuencias para datos agrupados, supongamos que en un
Archivo se desea conocer el número promedio de expedientes que son
revisados diariamente y la desviación media correspondiente, si se tiene
una muestra de 40 días:
CLASES
13 17
18 22
23 27
28 32
33 37
38 42
f Mc fMc
3 15 45
1 20 20
4 25 100
11 30 330
8 35 280
13 40 520
40
1295
⏐Mc-X⏐
17
12
7
2
3
8
f⏐ Mc-X ⏐
51
12
28
22
24
104
241
_
1295
El número promedio de expedientes revisados durante 40 días es: X = --------- = 32.3
aproximadamente 32
40
La fórmula para calcular la desviación media en datos agrupados en
una distribución con intervalos es:
∑f⏐Mc-X⏐
DM = ---------------n
por lo que sustituyendo :
241
DM = --------- = 6.02 redondeando
es 6
40
CONCLUSIÓN: En promedio se revisan 32 expedientes diariamente
con una desviación promedio de más o de menos 6 expedientes diarios.
121
¿QUÉ HE APRENDIDO?
La siguiente tabla muestra el tiempo en minutos que tarda una persona
en realizar los trámites necesarios para recibir un libro para préstamo a
domicilio:
CLASES
7-9
10-12
13-15
16-18
19-21
TOTAL
f
5
15
12
8
5
45
1) Calcula el promedio y la desviación media e interprétala.
122
Estadística Descriptiva
4.2.4 VARIANZA
4.2.5 DESVIACIÓN ESTÁNDAR
CÁLCULO DE LA VARIANZA O VARIANCIA (Var(X)) PARA DATOS
NO AGRUPADOS
Es una medida de dispersión en donde se calculan los cuadrados de
las desviaciones entre los valores de la variable y la media (xi - X)2 y su
suma se divide entre n-1 si se trata de una muestra de tamaño n y entre N
si se trata de una población:
Muestra tamaño n:
n
_
∑(xi - X)2
i=1
2
VAR(X) = S = ---------------------- VARIANZA MUESTRAL
n -1
Población tamaño N:
n
_
∑(xi - X)2
i=1
VAR(X) = σ2 = ---------------------- VARIANZA POBLACIONAL
N
En una biblioteca se ha reportando la pérdida de 36 libros distribuidos
de la siguiente manera: enero 4, febrero 5, marzo 9, abril 10, mayo 5 y junio
3.
En este ejercicio podemos trabajar con la lista o con la tabla, para
agilizar los cálculos utilicemos la tabla:
NÚMERO DE LIBROS EXTRAVIADOS EN LA BIBLIOTECA
DURANTE EL PERÍODO ENERO-JUNIO
--Al elevar al cuadrado las
MESES
xi
xi -X
(xi - X)2
desviaciones reales de la
ENERO
4
4-6=-2
4
variable con respecto a la
FEBRERO
5
5-6=-1
1
media se evita el manejo
MARZO
9
9-6=3
9
de números negativos, ya
ABRIL
10
10-6=4
16
que todo número elevado
MAYO
5
5-6=-1
1
al cuadrado es positivo.
JUNIO
3
3-6=-3
9
36
0
40
La suma de los desvíos es cero
_
36
123
El promedio de libros extraviados es X = ------- = 6
6
Usemos la fórmula para calcular la varianza respectiva:
_
40
40
∑(xi - X)2
2
VAR(X) = S = ---------------------- = ---------------- = -------- = 1.14
n -1
36-1
35
Un ejemplo más lo realizaremos con la tabla de calificaciones del
grupo A, tomando en cuenta que su media es 8.
CALIFICACIONES DEL GRUPO A
CALIFICACIÓN
f
xi-X
(xi - X)2 f(xi - X)2
6
1
-2
4
4
7
2
-1
1
2
8
4
0
0
0
9
2
1
1
2
10
1
2
4
4
10
12
12
S2A = -------- = 1.2
10
De igual manera que se hicieron los cálculos de la varianza para el
grupo A, encuentra la misma medida de dispersión para el grupo B
completando la tabla que aparece a continuación:
GRUPO
B
6
7
7
7
7
8
9
9
10
10
CALIFICACIONES DEL GRUPO B
CALIFICACIÓN
f
xi-X
(xi - X)2 f(xi - X)2
6
7
8
9
10
S2B = -------- =
Como te habrás dado cuenta mientras mayor es la dispersión, mayor
es la varianza, por ello es que en este caso la varianza mayor es del grupo
___________
124
Estadística Descriptiva
La varianza es una excelente medida que indica la dispersión de los
datos, el único inconveniente es que sus unidades son cuadradas lo cual no
tiene ningún sentido, con el propósito de superar este problema se utiliza la
DESVIACIÓN ESTÁNDAR, que se define como la raíz cuadrada de la
varianza y es la medida de variabilidad que veremos a continuación.
CÁLCULO DE LA DESVIACIÓN TÍPICA O ESTÁNDAR PARA
DATOS NO AGRUPADOS
Esta medida de dispersión es muy parecida a la desviación media,
tiene como base la media y sus unidades de medida son iguales a las
unidades de los datos, por ejemplo si los datos son libros o expedientes, la
desviación estándar también son libros o expedientes según corresponda.
En términos generales podemos decir que la desviación estándar
representa la “variabilidad promedio” de los datos de una distribución con
respecto a la media, de tal manera que, mientras mayor sea la dispersión
alrededor de la media, mayor será la desviación estándar.
Al calcular la varianza de las calificaciones del grupo A obtuvimos:
12
S2 A= -------- = 1.2
10
Es claro entonces que la desviación estándar para una muestra de 10
calificaciones es:
SA = √1.2 = 1.09
Calcula la desviación estándar para el grupo B:
SB =
125
CÁLCULO DE LA VARIANZA Y DESVIACIÓN ESTÁNDAR PARA
DATOS AGRUPADOS
Consideremos nuevamente la información de la tabla que muestra el
número de expedientes que son revisados durante 40 días en un Archivo:
CLASES
13
17
18
22
23
27
28
32
33
37
38
42
f
3
1
4
11
8
13
40
Mc
15
20
25
30
35
40
fMc
45
20
100
330
280
520
1295
La fórmula que se utiliza es:
n
n
∑fMc2
∑ fMc
i=1
i=1
VAR(X) = S2 = --------------- - ---------------n
n
∑f
∑f
i=1
i=1
2
A la tabla anterior le agregamos las columnas Mc2 y fMc2
CLASES
13
17
18
22
23
27
28
32
33
37
38
42
f
3
1
4
11
8
13
40
Mc
15
20
25
30
35
40
Mc2
225
400
625
900
1225
1600
fMc
45
20
100
330
280
520
1295
fMc2
675
400
2500
9900
9800
20800
44075
1677025
Sustituyendo los valores:
44075
(1295)2
1677025
VAR(X) = S2 = --------------- - ---------------- = 1101.875 - --------------40
(40)2
1600
126
Estadística Descriptiva
S2 = 1101.875 - 1048.1406 = 53.73
S2 = 53.73 sacando raíz encontramos el valor de la desviación
estándar
S = 7.3
Ray I. Carpenter en su libro Métodos Estadísticos para Bibliotecarios
dice: “Por ser una medida de dispersión estandarizada, la desviación
estándar se puede emplear para comparar la igualdad o la desigualdad de
dos o más grupos. Si los grupos son comparables, cuanto mayor sea la
diferencia en las desviaciones estándar, mayor será la desigualdad. Con
frecuencia, la sola comparación de las desviaciones estándar puede
conducir a interpretaciones incorrectas. Un método para evitar lo anterior es
el coeficiente de variación”.
127
4.2.6 COEFICIENTE DE VARIACIÓN
También conocido como DISPERSIÓN RELATIVA (CV) es un
indicador expresado en porcentaje de la dispersión de dos o más conjuntos
que se comparan entre sí, considerando la desviación estándar y la media
de los datos observados.
Coeficiente de variación muestral
S
CV= ---------(100)
X
_
donde S es la desviación estándar de la muestra y X la media.
Coeficiente de variación poblacional
σ
CV= ---------(100)
µ
σ es la desviación estándar de la población y µ la media.
Un ejemplo que muestra claramente la utilidad del coeficiente de
variación es cuando se desean comparar los presupuestos de una
biblioteca o de un archivo durante 2 años, a fin de averiguar en cuál de los
dos períodos (1995 ó 1996) las cantidades asignadas a las diferentes áreas
fue más homogénea, entendiéndose ésta como aquella distribución en que
las cantidades bajas, intermedias y altas son muy parecidas.
AÑO
1995
PRESUPUESTO
PROMEDIO
X
$14,400
DESVIACIÓN
ESTÁNDAR
S
$1,200
1996
$21,000
$1,500
1
CV1995 = ------ (100) = 8.33%
12
>
COEFICIENTE DE
VARIACIÓN
V
1,200/14,400=
12/144=2/24=1/12
1,500/21,000=
15/210=3/42=1/14
1
CV1996 = ------ (100) = 7.14%
14
En términos absolutos se tiene que la desviación estándar es mayor en
1996, sin embargo, desde un punto de vista relativo existe menos
dispersión en ese mismo período, según podemos observar en los dos
coeficientes de variación, ya que el menor de ellos pertenece a la
distribución más homogénea.
128
Estadística Descriptiva
El porcentaje de disminución de la variabilidad o dispersión se
encuentra a través de la tasa de cambio en donde se deben considerar los
coeficientes de variación al inicio del período (.0833) y al final del período
(.0714):
.071-.083
.-012
Tasa de cambio = ------------------- = ----------- = -0.144
.083
.083
Esto significa que en 1996 se tuvo una disminución del 14% de
dispersión con respecto a 1995.
129
4.2.7 TEOREMA DE CHEBYSHEV
La desviación estándar permite medir las variaciones con respecto a la
media de los valores de las observaciones, ya que mientras más pequeña
sea es más probable obtener un valor cercano a la media y viceversa, se
tiene mayor probabilidad de obtener un valor más alejado a la media a
medida que ésta es mayor, para encontrar estas variaciones en cualquier
distribución, se utiliza el Teorema de Chebyshev que dice:
La proporción de cualquier conjunto de valores que caen dentro de k
desviaciones típicas medidas a partir de la media es al menos 1 - 1/k2, en
donde k es cualquier número mayor de 1.
Si consideramos k=2 (2 desviaciones típicas o estándar), tendremos
que los valores dentro del intervalo formado por las dos desviaciones
estándar medidas a partir de la media es 1-1/22 = 1 - ¼ = ¾, esto indica que
dentro de 2 desviaciones estándar de la media, siempre se encuentra al
menos el 75% ( 75% como mínimo) de los datos.
De igual forma si k=3 al menos 8/9 (88% o más) de los datos caen
dentro del intervalo (X-3S, X+3S).
Retomando el ejercicio en donde se conoce el número de libros o
expedientes prestados durante 50 días, verifiquemos el Teorema que nos
ocupa:
43
44
45
47
48
48
50
51
53
53
130
54
54
55
56
56
56
56
57
57
58
58
59
60
60
60
60
61
61
61
62
62
62
63
64
64
65
65
65
65
65
67
67
68
69
70
70
72
75
79
80
Estadística Descriptiva
Calculando las columnas necesarias para encontrar la desviación
estándar:
CLASES
73-77
68-72
63-67
58-62
53-57
48-52
43-47
f
3
5
10
13
11
4
4
50
Mc
75
70
65
60
55
50
45
Mc2
5625
4900
4225
3600
3025
2500
2025
181800
S = ------------- 30
2
2
S = 3636
fMc
225
350
650
780
605
200
180
2990
fMc2
16875
24500
42250
46800
33275
10000
8100
181800
_
X ≅ 60
(2990)2
--------------(50)2
8940100
- ------------2500
S2 = 3636 - 3576.04 = 59.96
entonces S = 7.74
Al tomar 2 desviaciones estándar se tiene el intervalo:
(X - 2s, X + 2s) = (60 - 2(7.74), 17 + 2(7.74)) = (44.52, 75.48)
Si consideramos al intervalo (45, 75) sin tomar los extremos, por el
Teorema de Chebyshev dentro de él cae al menos el 75% del total de
datos, esto quiere decir que pueden caer 75% o más.
Al calcular el 75% de 50 que es el total de datos, se encuentra que en
dicho intervalo deben caer aproximadamente 38 datos o más, para verificar
este porcentaje contemos los datos en la lista ordenada:
43
44
45
47
48
48
50
51
53
53
54
54
55
56
56
56
56
57
57
58
58
59
60
60
60
60
61
61
61
62
62
62
63
64
64
65
65
65
65
65
67
67
68
69
70
70
72
75
79
80
Los 44 valores en negrita son los que se
encuentran dentro del intervalo (45, 75) y son
más del 75% del total.
131
_
Conociendo la media X = 60 y la desviación estándar S=7.74,
considera 3 desviaciones estándar y encuentra:
a) Intervalo que contiene al menos el 88% del total de datos
________________________________________________
b) El 88% de 50
________________________________________________
c) En la lista ordenada destaca subrayando en color los datos que
caen en el intervalo:
43
44
45
47
48
48
50
51
53
53
54
54
55
56
56
56
56
57
57
58
58
59
60
60
60
60
61
61
61
62
62
62
63
64
64
65
65
65
65
65
67
67
68
69
70
70
72
75
79
80
Después de calcular lo que se te pide, indica si se cumple o no el
Teorema de Chebyshev.
________________________________________________
LECTURA 4
Como un refuerzo a lo que acabas de aprender, te recomiendo leer el
libro Fundamentos de la Estadística en la Investigación Social escrito por
Jack Levin de la página 55 a la 70, incluido al final de esta guía, después de
la lectura escribe el resumen correspondiente.
132
Estadística Descriptiva
Elabora el Resumen de la Unidad 4 identificando y completando el
siguiente mapa conceptual, al final de la guía lo encontrarás resuelto, de ser
posible, confronta tus respuestas y corrígelas en caso de ser erróneas.
DESCRIPCIÓN DE LOS DATOS A
TRAVÉS DE LAS MEDIDAS DE:
__________________________________
Valores centrales de una distribución que
representan a todos los datos.
__________________.-Suma de valores de
todas las observaciones divida entre el
número de observaciones realizadas
DATOS NO AGRUPADOS:
Muestra
Población
_
∑X
∑X
X =--------µ = ----------n
N
DATOS AGRUPADOS:
_
∑ _______
∑_______
X =---------------µ = ----------n
N
__________________________________
Evalúan la variabilidad o dispersión de los
datos.
RANGO___________________________
____________________________
R = Valor máximo - Valor mínimo
RANGO ______________ diferencia entre
los valores del primero y tercer cuartil:
Q = Q3 - Q1
______________________:
n/4 - F1
Q1= Li + ( --------------- ) A
f1
Para Q2 se toma 2n/4 y para Q2, 3n/4
___________ es el valor (o valores) de
la(s) variable(s) que ocupa (n) el (los)
lugar(es) central(es) de los datos ordenados
por magnitud:
DATOS NO AGRUPADOS:
a) Número par de datos es el promedio de
valores centrales
b) Número impar de datos es ___________
______________________________
DATOS AGRUPADOS:
n/2 -F
Md = Li + ( ---------- ) A
f
___________________es el promedio de
las desviaciones a partir de la media:
__________valor (o valores) de la variable
que se presenta(n) con mayor frecuencia.
DATOS NO AGRUPADOS:
a) Ordenar en forma ascendente y realizar
conteo
__________________ es la raíz cuadrada
del promedio de las desviaciones con
respecto a la media elevadas al cuadrado.
DATOS NO AGRUPADOS:
_
√∑(xi - X)2
S = ----------------- muestral
n-1
√∑fMc2
S = ----------------- muestral
n-1
DATOS AGRUPADOS:
d1
Md = Li + ( ---------- ) A
d1+d1
Continúa Resumen de la Unidad 4:
DATOS NO AGRUPADOS:
_
∑⏐xi -X⏐
DM = -----------n
DATOS AGRUPADOS:
_
∑f⏐Mc-X⏐
DM=-------------n
133
DESCRIPCIÓN DE LOS DATOS A
TRAVÉS DE LAS MEDIDAS DE:
__________________________________
Valores centrales de una distribución que
representan a todos los datos.
__________________________________
Evalúan la variabilidad o dispersión de los
datos.
______________________es el promedio
de las desviaciones con respecto a la media
elevadas al cuadrado.
DATOS NO AGRUPADOS:
_
∑(xi - X)2
S2 = ----------------- muestral
n-1
∑fMc2
S2 = ----------------- muestral
n-1
___________________________________
________________, si X es la media y S la
desviación estándar de una muestra, su
fórmula es:
CV = --------(100)
Permite comparar la homogeneidad de los
datos en dos conjuntos.
______________________ utiliza la desviación
típica de un conjunto de observaciones para
medir las variaciones de los datos con respecto a la
media de tal forma que mientras más pequeña sea
la desviación, es más probable obtener un valor
cercano a la media y por el contrario, mientras
mayor sea la desviación es más probable obtener
un valor alejado de la media.
Si se consideran 2 desviaciones estándar:
en el intervalo (X - 2S, X + 2S) cae al menos el
_____% de los datos.
Si se consideran 3 desviaciones estándar:
en el intervalo (X -3S, X + 3S) cae como mínimo
el _____% de los datos.
134
Estadística Descriptiva
EVALUACIÓN
1) Completa la siguiente tabla, calcula las Medidas de Tendencia
Central de la distribución obtenida al evaluar a 50 alumnos en la asignatura
de Investigación de Campo I y contesta lo que se te pregunta en los incisos:
CALIFICACIÓN NÚMERO DE
X
ALUMNOS
f
5
6
6
5
7
11
8
12
9
14
10
2
50
fX
fa
a) Como la media es ________ entonces los 50 alumnos tienen esta
calificación como representativa del grupo.
b)La _________ indica que el número más numeroso de estudiantes
tiene calificación de _______
c) El valor central de la distribución es la ____________ que tiene el
valor de __________ e indica que el 50% de los alumnos (25 alumnos)
obtuvieron calificaciones entre ________ y _____________.
135
2) En un Archivo Histórico, al tomar una muestra representativa de 142
expedientes en forma arbitraria y contar el número de hojas se obtuvo la
siguiente información:
CLASES
(HOJAS)
X
5 -19
20-34
35-49
50-64
65-79
NÚMERO DE
EXPEDIENTES
f
26
18
14
36
48
142
Calcula las medidas de tendencia central y escríbelas anotando una
conclusión en cada caso:
a)
Media:
_______________________________________________________
Conclusión:
_____________________________________________________
b)
Moda:
________________________________________________________
Conclusión:
_____________________________________________________
c)
Mediana:
______________________________________________________
Conclusión:
_____________________________________________________
d) Calcula la desviación media e interprétala:
El Jefe del Archivo desea modificar la cubierta de cada expediente y
tiene la opción de comprar carpetas de un sólo tipo que puede ser:
- Con capacidad para 50 hojas
- Con capacidad para 70 hojas
Tomando en consideración los resultados de las medidas de tendencia
central que obtuviste ¿cuál de los dos tipos de carpetas le sugerirías a tu
jefe
que
comprara
y
por
qué?________________________________________________________
___
136
Estadística Descriptiva
137
3) La siguiente gráfica simétrica tiene un nombre especial por su forma,
se le denomina “normal”, une con una recta el lugar en donde consideras
que se encuentran las medidas de tendencia central:
CURVA SIMÉTRICA
MESOCÚRTICA
(NORMAL)
10
8
6
4
Media
Moda
Mediana
2
C A LIF I C A C I ÓN
9
6
3
0
0
a) ¿Qué valor crees que tenga la Media?
_____
__________________________________
____
ENVÍA A TU ASESOR
¡FELICIDADES!
Ahora que has finalizado la materia, espero que continúes
con ímpetu el resto de la carrera. Bien por tí
138
Estadística Descriptiva
RESUMEN DE LA UNIDAD I
ESTADÍSTICA
OBJETO
Inferir el comportamiento
de una población a través
del análisis de una muestra.
Ciencia de la recopilación,
clasificación, presentación e
interpretación de datos.
SE CLASIFICA EN
DESCRIPTIVA
Incluye obtención, organización y
presentación de datos, así como la
descripción numérica que muestra
el comportamiento de una población
o muestra.
TIENEN COMO BASE
UNA
POBLACIÓN QUE ES:
Un conjunto de individuos u objetos de
interés bien definidos. Su tamaño es N y
sus características son descritas por
parámetros como el porcentaje.
PUEDE SER:
1) FINITA
Tiene primer y
último elemento
2) INFINITA
Tiene primer
elemento pero no
último
INFERENCIAL
Está integrada por métodos descriptivos
que permiten la generalización del
comportamiento de una población a
partir de los resultados obtenidos de una
muestra que la represente.
MUESTRA REPRESENTATIVA
Parte de la población que la representa, su
tamaño se indica con n. Los estadísticos o
O UNA PARTE
estadígrafos son números que describen sus
características, un ejemplo es el promedio.
SUS CARACTERÍSTICAS
SE DENOMINAN
VARIABLES Y SON:
NOMINAL
CUALITATIVA
ORDINAL
DISCRETA
CUANTITATIVA
CONTINUA
CLASIFICÁNDOSE SEGÚN LAS SIGUIENTES
ESCALAS DE MEDICIÓN:*
- NOMINAL
- ORDINAL
- INTERVALO
- ABSOLUTA
*Escalas de medición:
a) Nominal.- Se utiliza como medida de identificación con variables nominales.
b) Ordinal.- Permite la manipulación de variables ordinales.
c) Intervalo o Absoluta:- Maneja variables cuantitativas.
139
RESUMEN DE LA UNIDAD 2
TIPOS DE DATOS
CATEGÓRICOS
Permiten agrupar por
categorías
ORDENADOS POR RANGO
Establecen un orden entre
categorías para compararlas
MÉTRICOS
Introducen medidas que
facilitan la comparación
DISTRIBUCIONES DE FRECUENCIA
POBLACIÓN O MUESTRA PEQUEÑA
SIMPLE CUYA ESTRUCTURA ES:
a) TITULO
b) PERÍODO DE TIEMPO
c)
d)
CATEGORÍAS
FRECUENCIA
A
B
f
f
SUMA DE f
g) PIE
TO T A L
e)
f) FUENTE
donde:
a) Título que explique brevemente el
contenido de la tabla
b) Fecha o período de tiempo en que se
efectuó la investigación
c) Encabezados de cada columna
d) Cuerpo que contiene la información de las
categorías
e) Final o total de las columnas
f) Fuente de la información
g) Observaciones importantes
a)
b)
c)
d)
140
ORDINALES
NOMINALES
CONTINUAS
DISCRETAS
POBLACIÓN O MUESTRA GRANDE
PARA DATOS AGRUPADOS CUYA
ESTRUCTURA ES:
CLASES f
Mc
fr
fa
far
a)
b)
c)
d)
e)
f)
donde:
a)Clases o intervalos formados por límite inferior
y límite superior
b) Frecuencia absoluta de cada clase
c) Marca de clase o punto medio del intervalo
d) Frecuencia relativa proporción de la frecuencia
de cada intervalo con respecto a la suma de
frecuencias absolutas
e)Frecuencia acumulada que indica el intervalo
donde se encuentra un dato específico
f)Frecuencia acumulada relativa proporción de la
frecuencia acumulada de cada intervalo con
respecto a la suma de frecuencias absolutas.
TIPO DE VARIABLES QUE UTILIZAN
D
a) CONTINUAS
b) DISCRETAS
Estadística Descriptiva
RESUMEN DE LA UNIDAD 3
TIPOS DE GRÁFICAS
GRÁFICA DE SECTORES:
Características:
a)Es una circunferencia en el primer cuadrante del plano
cartesiano donde a la frecuencia de cada categoría le
corresponde un sector
b) Representación gráfica de una tabla de distribución de
frecuencias simple
c) El número de categorías a considerar debe ser menor
que en el de barras
HISTOGRAMA
Características:
a) Son barras unidas que se trazan en el primer cuadrante
del plano cartesiano
b) Representación gráfica de una distribución de
frecuencias para datos agrupados
c) En el eje de las “X” se marcan los puntos medios de
cada intervalo
d) En el eje de las “Y” se consideran las frecuencias
correspondientes a cada intervalo
OJIVA PORCENTUAL:
Características:
a) Gráfica lineal trazada en el primer cuadrante del plano
cartesiano que tiene forma de “S”
b) Representación gráfica de una distribución de
frecuencias acumuladas para datos agrupados
c) En el eje de las “X” se marcan los límites reales
superiores de cada intervalo
d) En el eje de las “Y” se marcan las frecuencias
acumuladas correspondientes a cada intervalo
e) Permite hacer estimaciones del comportamiento de los
datos considerando uno en particular
DIAGRAMA DE BARRAS
Características:
a) Son barras del mismo ancho trazadas en el primer
cuadrante del plano cartesiano
b) Las barras deben estar separadas por espacios en
blanco
d) Representación gráfica de una tabla de distribución de
frecuencias simple
e) Pocas categorías
VARIABLES
CONSIDERADAS
a) Nominal
b) Ordinal
VARIABLES
CONSIDERADAS
a) Continuas
b) Discretas
VARIABLES
CONSIDERADAS
a) Continuas
b) Discretas
VARIABLES
CONSIDERADAS
a) Nominal
b) Ordinal
141
RESUMEN DE LA UNIDAD 3
TIPOS DE GRÁFICAS
POLÍGONO DE FRECUENCIAS:
Características:
a) Gráfica lineal trazada en el primer cuadrante del
plano cartesiano que une los puntos medios de cada
clase a la altura de su frecuencia correspondiente
b) Representación gráfica de una distribución de
frecuencias para datos agrupados
c) En el eje de las “X” se marcan los puntos medios
de cada intervalo, agregándose uno al inicio y otro al
final de los que se están considerando
d) En el eje de las “Y” las frecuencias
correspondientes a cada intervalo, agregándose dos en
cero que corresponden a las marcas de clase indicadas
en el inciso anterior.
VARIABLES
CONSIDERADAS
a) Continuas
b) Discretas
NOTA: Es recomendable que todas las gráficas tengan un título que describa brevemente la
información que está siendo representada, así como la fuente de información, ya que éstas deben
ser autoexplicativas; con excepción de la gráfica de sectores, todas deben contener un título en
cada uno de los ejes que indique el tipo de datos que se están representando.
142
Estadística Descriptiva
RESUMEN DE LA UNIDAD 4
DESCRIPCIÓN DE LOS DATOS A
TRAVÉS DE LAS MEDIDAS DE:
TENDENCIA CENTRAL
Valores centrales de una distribución que
representan a todos los datos.
DISPERSIÓN
Evalúan la variabilidad o dispersión de los
datos.
MEDIA ARITMÉTICA.-Suma de valores
de todas las observaciones divida entre el
número de observaciones realizadas
DATOS NO AGRUPADOS:
Muestra
Población
_
∑X
∑X
X =--------µ = ----------n
N
RANGO o amplitud total considera valores
extremos:
R = Valor máximo - Valor mínimo
DATOS AGRUPADOS:
_
∑fMc
∑fMc
X =----------µ = ----------n
N
RANGO INTERCUARTIL diferencia entre
los valores del primero y tercer cuartil:
Q = Q3 - Q1
CUARTILES:
n/4 - F1
Q1= Li + ( --------------- ) A
f1
Para Q2 se toma 2n/4 y para Q2, 3n/4
MEDIANA es el valor (o valores) de la(s)
variable(s) que ocupa (n) el (los) lugar(es)
central(es) de los datos ordenados por
magnitud:
DATOS NO AGRUPADOS:
a) Número par de datos es el promedio de
valores centrales
b) Número impar de datos es el dato central
DATOS AGRUPADOS:
n/2 -F
Md = Li + ( ---------- ) A
f
DESVIACIÓN MEDIA es el promedio de
las desviaciones a partir de la media:
MODA valor (o valores) de la variable que
se presenta(n) con mayor frecuencia.
DATOS NO AGRUPADOS:
a) Ordenar en forma ascendente y realizar
conteo
DESVIACIÓN TÍPICA O ESTÁNDAR es
la raíz cuadrada del promedio de las
desviaciones con respecto a la media
elevadas al cuadrado.
DATOS NO AGRUPADOS:
_
√∑(xi - X)2
S = ----------------- muestral
n-1
√∑fMc2
S = ----------------- muestral
n-1
DATOS AGRUPADOS:
d1
Md = Li + ( ---------- ) A
d1+d1
DATOS NO AGRUPADOS:
_
∑⏐xi -X⏐
DM = -----------n
DATOS AGRUPADOS:
_
∑f⏐Mc-X⏐
DM=-------------n
P
P
P
P
143
RESUMEN DE LA UNIDAD 4
DESCRIPCIÓN DE LOS DATOS A
TRAVÉS DE LAS MEDIDAS DE:
TENDENCIA CENTRAL
Valores centrales de una distribución que
representan a todos los datos.
DISPERSIÓN
Evalúan la variabilidad o dispersión de los
datos
VARIANZA O VARIANCIA es el
promedio de las desviaciones con respecto
a la media elevadas al cuadrado.
DATOS NO AGRUPADOS:
_
∑(xi - X)2
S2 = ----------------- muestral
n-1
∑fMc2
S2 = ----------------- muestral
n-1
:
P
P
P
P
P
P
P
P
COEFICIENTE DE VARIACIÓN O
DISPERSIÓN RELATIVA, si X es la
media y S la desviación estándar de una
muestra, su fórmula es:
S
CV = --------(100)
X
Permite comparar la homogeneidad de los
datos en dos conjuntos.
TEOREMA DE CHEBYSHEV utiliza la desviación típica de
un conjunto de observaciones para medir las variaciones de
los datos con respecto a la media de tal forma que mientras
más pequeña sea la desviación, es más probable obtener un
valor cercano a la media y por el contrario, mientras mayor
sea la desviación es más probable obtener un valor alejado de
la media.
Si se consideran 2 desviaciones estándar:
en el intervalo (X - 2S, X + 2S) cae al menos el 75% de los
datos
Si se consideran 3 desviaciones estándar:
en el intervalo (X -3S, X + 3S) cae como mínimo el 88% de
los datos
144
Estadística Descriptiva
145