Los infinitos en la teoría de los conjuntos. La correspondencia
Anuncio

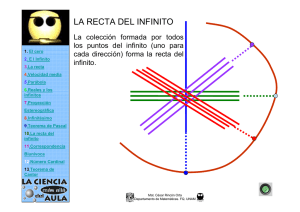
Algunos Infinitos en la matemática 1. El cero Los infinitos en la teoría de los conjuntos. La correspondencia biunívoca entre dos conjuntos. f 2. E l Infinito 3.La recta 4.Velocidad media 5.Parábola 6.Reales y los infinítos es biunívoca, si establece una correspondencia 1-1 entre los elementos de A y los de B, tal que elementos distintos van a elementos distintos y en esa correspondencia se agotan los elementos de cada conjunto. Es claro que entonces, si existe una correspondencia tal entre dos conjuntos el “número de elementos” (igual cardinalidad) de cada uno de ellos debe ser el mismo. 7.Proyección A=B Estereográfica 8.Infinitésimo 9.Teorema de Pascal 10.La recta del infinito 11.Correspondencia A B f a F(a) Biunívoca 12.Número Cardinal 13.Teorema de Cantor Mat. César Rincón Orta Departamento de Matemáticas. FQ. UNAM Algunos Infinitos en la matemática 1. El cero 2. E l Infinito 3.La recta 4.Velocidad media 5.Parábola 6.Reales y los infinítos 7.Proyección Estereográfica 8.Infinitésimo 9.Teorema de Pascal 10.La recta del infinito 11.Correspondencia Biunívoca 12.Número Cardinal 13.Teorema de Cantor UNA CORRESPONDENCIA RARA 0 1 2 3 0 2 4 6 M M n 2n M M La correspondencia que se muestra es biunívoca “biyectiva”. ¿Hay más números naturales que números naturales pares? Note que 2N esta contenido en N pero no lo cubre totalmente ( la contención es propia). Mat. César Rincón Orta Departamento de Matemáticas. FQ. UNAM Algunos Infinitos en la matemática 1. El cero 2. E l Infinito 3.La recta 4.Velocidad media 5.Parábola Def. Un conjunto A es infinito si tiene algún subconjunto propio con el mismo número de elementos. A es infinito ⇔ ∃B ⊂ A , B ≠ A y A = B . 6.Reales y los infinítos 7.Proyección Estereográfica 8.Infinitésimo 9.Teorema de Pascal Def. Un conjunto es finito, si no es infinito. 10.La recta del infinito 11.Correspondencia Biunívoca 12.Número Cardinal ES INFINITO 13.Teorema de Cantor Mat. César Rincón Orta Departamento de Matemáticas. FQ. UNAM