6. Geometría del tetraedro

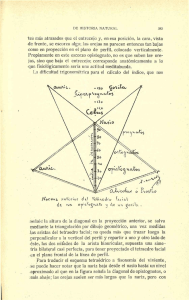
EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO
87
6. GEOMETRÍA DEL TETRAEDRO
Volumen del tetraedro
El volumen de un tetraedro es la sexta parte del volumen del paralelepípedo que
lo contiene (véase figura 5.6). El volumen del paralelepípedo es igual al producto
exterior de tres aristas cualesquiera no paralelas. El resultado es positivo o negativo
según sea la orientación de las tres segmentos igual u opuesta a la de los vectores de los
ejes de coordenadas. Para un tetraedro de vértices A, B, C y D su volumen viene dado
por:
V =
1
1
AB ∧ AC ∧ AD = AB ∧ BC ∧ CD
6
6
También pueden descomponerse los segmentos en función de los vectores posición lo
que da como resultado:
V = −A ∧ B ∧ C + A ∧ B ∧ D − A ∧ C ∧ D + B ∧ C ∧ D
Medianas y baricentro
Sean A, B, C y D cuatro vértices del tetraedro. Se define una mediana como el
segmento que va desde un vértice (por ejemplo A) al baricentro de su cara opuesta BCD.
En total hay cuatro medianas, una para cada vértice. Estas cuatro medianas se cortan en
un punto llamado baricentro del tetraedro, como se demuestra a continuación. Por
ejemplo, la intersección G de la mediana del
vértice A con la del vértice B (figura 6.1), en caso
de que exista (en el espacio podrían no cortarse),
vendrá dada por las ecuaciones:
B+C + D

G = α A + (1 − α )
3

A+C + D
G = β B + (1 − β )
3

Igualando encontramos:
α A + (1 − α )
B+C + D
A+C + D
= β B + (1 − β )
3
3
Figura 6.1
1− β 

1− α

 −α + β 
 −α + β 
−β+C 
A α −
+B
+D
=0
3 

 3

 3 
 3 
Como los cuatro vértices no son coplanares, es decir son independientes, todos los
coeficientes han de anularse y, por tanto, la solución es α = β = 1 / 4 , de donde se sigue
la ecuación del baricentro:
RAMON GONZÁLEZ CALVET
88
G=
A+ B+C + D
4
Esta fórmula es invariante bajo permutación cíclica de los vértices, luego
cualquier otra pareja de medianas se cortan también en el mismo punto G, el baricentro.
Circuncentro, centro de la esfera circunscrita
Sea O el centro de la esfera circunscrita al tetraedro ABCD, su circuncentro
(figura 6.2). La condición que debe cumplir es que la distancia del circuncentro O a los
cuatro vértices sea la misma:
OA2 = OB 2 = OC 2 = OD 2
Desarrollamos la primera ecuación:
( A − O )2 = (B − O )2
⇔
A2 − 2 A ⋅ O + O 2 = B 2 − 2 B ⋅ O + O 2
⇔
2O ⋅ AB = B 2 − A 2
Aislando O tenemos:
2O ⋅ (B − A) = B 2 − A2
Con esta ecuación y las análogas obtenidas de las otras condiciones, llegamos a un
sistema de ecuaciones lineales:

B 2 − A2
O
AB
⋅
=

2

2
C − B2

O
BC
⋅
=

2

2
D
−C2
O ⋅ CD =

2
Para resolver un sistema de ecuaciones lineales
de la forma:
a ⋅ u = d

b ⋅ u = e
c ⋅ u = f

escribamos explícitamente las componentes de los vectores a, b, c y u:
a x u x + a y u y + a z u z = d

 bxu x + by u y + bz u z = e
c u + c u + c u = f
y y
z z
 x x
Figura 6.2
EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO
89
Por la regla de Cramer tenemos:
ux =
uy =
uz =
d
ay
az
e
by
bz
f
cy
cz
ax
ay
az
bx
cx
by
cy
bz
cz
ax
d
az
bx
cx
e
f
bz
cz
ax
ay
az
bx
by
bz
cx
cy
cz
ax
ay
d
bx
by
e
cx
cy
f
ax
ay
az
bx
cx
by
cy
bz
cz
d
=
by
bz
cy
cz
−d
=
d
=
−e
bz
cx
cz
by
cx
cy
az
cy
cz
+ f
det (a, b, c )
bx
bx
ay
+e
ax
az
cx
cz
ax
ay
cx
cy
az
by
bz
−f
det (a, b, c )
−e
ay
+ f
det (a, b, c )
ax
az
bx
bz
ax
ay
bx
by
Estos tres resultados se pueden reunir en la igualdad:
u = (d b ∧ c + e c ∧ a + f a ∧ b ) (a ∧ b ∧ c )
−1
Así pues, la solución del sistema de ecuaciones para el circuncentro es:
[(
)
(
)
(
]
)
O = B 2 − A 2 BC ∧ CD + C 2 − B 2 CD ∧ AB + D 2 − C 2 AB ∧ BC (2 AB ∧ BC ∧ CD )
−1
Démosle una expresión simétrica bajo permutación cíclica:
[
]
−1
[
]
−1
O = − A 2 BC ∧ CD − B 2 CD ∧ AC − C 2 AB ∧ BD + D 2 AB ∧ BC (2 AB ∧ BC ∧ CD )
O = − A 2 BC ∧ CD + B 2 CD ∧ DA − C 2 DA ∧ AB + D 2 AB ∧ BC (2 AB ∧ BC ∧ CD )
Cuando se realiza una permutación cíclica de los vértices, A → B , B → C , C → D ,
D → A , todos los términos del primer paréntesis cambian de signo. Ello es debido al
cambio de la orientación del tetraedro, que cambia también el signo del volumen
AB ∧ BC ∧ CD , con lo cual el circuncentro O queda invariante.
RAMON GONZÁLEZ CALVET
90
Punto de Monge
El punto de Monge M es la intersección de los planos que pasan por el punto
medio de cada arista y son perpendiculares a la arista opuesta. Como hay seis aristas,
hay seis planos distintos. El punto M es la intersección de tres de estos planos pero los
otros tres planos también los cortan en el mismo punto M como demostraremos a
continuación.
C+D
Puesto que el punto M pertenece al plano que pasa por el punto medio
de
2
la arista CD y es perpendicular a la arista AB cumplirá la ecuación:
MC + MD
⋅ AB = 0
2
Puesto que el punto M también pertenece al plano que pasa por el punto medio
A+ D
2
de la arista AD y es perpendicular a la arista BC cumplirá la ecuación:
MA + MD
⋅ BC = 0
2
Finalmente, puesto que el punto M pertenece también al tercer plano que pasa por el
A+ B
punto medio
de la arista AB y es perpendicular a CD cumplirá la ecuación:
2
MA + MB
⋅ CD = 0
2
Así pues, el punto M intersección de estos tres planos viene dado por el sistema de
ecuaciones:
 MC + MD
⋅ AB = 0

2
 MA + MD
⋅ BC = 0

2

 MA + MB ⋅ CD = 0

2
Si sumamos un par de ecuaciones, por ejemplo la primera y la segunda, obtenemos:
(MC + MD ) ⋅ AB + (MA + MD ) ⋅ BC = MC ⋅ AB + MD ⋅ AC + MA ⋅ BC
= C ⋅ B − M ⋅ B − C ⋅ A + M ⋅ A + MD ⋅ AC + A ⋅ C − M ⋅ C − A ⋅ B + M ⋅ B
= C ⋅ B + M ⋅ A + MD ⋅ AC − M ⋅ C − A ⋅ B = MB ⋅ AC + MD ⋅ AC = 0
EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO
91
MB + MD
⋅ AC = 0
2
B+D
y es perpendicular a AC .
2
Análogamente, las sumas de las otras dos parejas rinden ecuaciones que demuestran que
M también pertenece a los otros dos planos. Así pues, los seis planos se cortan en un
solo punto, el punto de Monge M.
Si aislamos el punto de Monge en el sistema de ecuaciones encontramos:
Es decir, M pertenece también al plano que pasa por
C+D

 M ⋅ AB = 2 ⋅ AB

A+ D
⋅ BC
M ⋅ BC =
2

 M ⋅ CD = A + B ⋅ CD

2
Según la resolución de un sistema de ecuaciones que hemos desarrollado antes, la
solución de este sistema es:
D+ A
A+ B

C + D
−1
M =
⋅ AB BC ∧ CD +
⋅ BC CD ∧ AB +
⋅ CD AB ∧ BC  ( AB ∧ BC ∧ CD )
2
2
 2

que es una fórmula invariante bajo permutación cíclica de los vértices.
Recta de Euler del tetraedro
Recordemos que el circuncentro O y el punto de Monge M vienen dados por
los sistemas de ecuaciones:

B 2 − A2
 O ⋅ AB =
2

C 2 − B2

 O ⋅ BC =
2

2
2
O ⋅ CD = D − C

2
C+D

 M ⋅ AB = 2 ⋅ AB

A+ D
⋅ BC
M ⋅ BC =
2

 M ⋅ CD = A + B ⋅ CD

2
Sumando ambos sistemas obtenemos:

B 2 − A2 C + D
(
)
+
⋅
=
+
⋅ AB
O
M
AB

2
2

C 2 − B2 A + D

(
)
+
⋅
=
+
⋅ BC
O
M
BC

2
2

2
2
(O + M ) ⋅ CD = D − C + A + B ⋅ CD

2
2
⇔
A+ B+C + D
O + M
⋅ AB
 2 ⋅ AB =
4
 O + M
A+ B+C + D
⋅ BC =
⋅ BC

2
4

 O + M ⋅ CD = A + B + C + D ⋅ CD
 2
4
RAMON GONZÁLEZ CALVET
92
De donde se concluye que el baricentro G es el punto medio del circuncentro O y del
punto de Monge M (figura 6.3):
O+ M A+ B+C + D
=
=G
2
4
Si, en cambio, restamos ambos sistemas encontramos:
− A− B+C + D

⋅ AB
OM ⋅ AB =
2

A− B−C + D
⋅ BC
 OM ⋅ BC =
2

 OM ⋅ CD = A + B − C − D ⋅ CD
2

⇔
Figura 6.3
− DA + BC

⋅ AB
OM ⋅ AB =
2

− AB + CD
⋅ BC
OM ⋅ BC =
2

 OM ⋅ CD = DA − BC ⋅ CD
2

cuya solución es:
− AB + CD
DA − BC
 − DA + BC

OM = 
⋅ AB BC ∧ CD +
⋅ BC CD ∧ AB +
⋅ CD AB ∧ BC 
2
2
2


−1
( AB ∧ BC ∧ CD )
El producto geométrico permite escribir el primer paréntesis en una forma más
simétrica:
OM = ( AB BC CD DA − BC CD DA AB + CD DA AB BC − DA AB BC CD )
(4 AB ∧ BC ∧ CD )−1
La recta de Euler de un tetraedro es la recta que contiene al baricentro G, al
circuncentro O y al punto de Monge M. Su vector director es OM y su expresión es
invariante bajo permutación cíclica de los vértices del
tetraedro, aunque cada permutación cambie los signos
de cada paréntesis.
Incentro
El incentro I es el punto que está a la misma
distancia de las cuatro caras del tetraedro (figura 6.4).
Supongamos, por analogía con el incentro de un
triángulo, que el incentro I de un tetraedro con
vértices ABCD viene dado por la siguiente fórmula
invariante bajo permutación cíclica de los vértices:
I=
A BC ∧ CD + B CD ∧ DA + C DA ∧ AB + D AB ∧ BC
BC ∧ CD + CD ∧ DA + DA ∧ AB + AB ∧ BC
Calculemos los vectores que van de los vértices A y B al incentro I:
Figura 6.4
EL ÁLGEBRA GEOMÉTRICA DEL ESPACIO Y TIEMPO
AI = I − A =
BI =
93
AB CD ∧ DA + AC DA ∧ AB + AD AB ∧ BC
BC ∧ CD + CD ∧ DA + DA ∧ AB + AB ∧ BC
BA CD ∧ DA + BC DA ∧ AB + BD AB ∧ BC
BC ∧ CD + CD ∧ DA + DA ∧ AB + AB ∧ BC
Y ahora calculemos los siguientes productos exteriores:
AB ∧ AC ∧ AI =
AC ∧ AD ∧ AI =
AD ∧ AB ∧ AI =
BC ∧ BD ∧ BI =
AB ∧ AC ∧ AD AB ∧ BC
BC ∧ CD + CD ∧ DA + DA ∧ AB + AB ∧ BC
AC ∧ AD ∧ AB CD ∧ DA
BC ∧ CD + CD ∧ DA + DA ∧ AB + AB ∧ BC
AD ∧ AB ∧ AC DA ∧ AB
BC ∧ CD + CD ∧ DA + DA ∧ AB + AB ∧ BC
BC ∧ BD ∧ BA CD ∧ DA
BC ∧ CD + CD ∧ DA + DA ∧ AB + AB ∧ BC
para comprobar que efectivamente la fórmula propuesta para I cumple la condición de
equidistancia a las cuatro caras del tetraedro:
r=
AB ∧ AC ∧ AI
AB ∧ BC
=
AC ∧ AD ∧ AI
CD ∧ DA
=
AD ∧ AB ∧ AI
DA ∧ AB
=
BC ∧ BD ∧ BI
BC ∧ BD
ya que AB ∧ AC ∧ AD = AC ∧ AD ∧ AB = AD ∧ AB ∧ AC = − BC ∧ BD ∧ BA . Estos
cocientes son justamente el radio r de la esfera inscrita en el tetraedro y su valor es igual
a:
r=
AB ∧ AC ∧ AD
BC ∧ CD + CD ∧ DA + DA ∧ AB + AB ∧ BC
=
3V
S
ya que el numerador es seis veces el volumen V del tetraedro y el denominador es el
doble de la superficie S del tetraedro, la suma de las áreas de sus caras.
Ejercicios
6.1 Demuéstrese que los 3 segmentos que unen los puntos medios de las aristas opuestas
de un tetraedro se cruzan en el baricentro.
6.2 Demostrar que el radio R de la esfera circunscrita a un tetraedro ABCD viene dado
por:
RAMON GONZÁLEZ CALVET
94
R=
AB 2 BC ∧ CD + BC 2 CD ∧ DA + CD 2 AB ∧ BC
2 AB ∧ BC ∧ CD
6.3 Demuéstrese la afirmación de que el vector de la recta de Euler de un tetraedro
ABCD es:
OM = ( AB BC CD DA − BC CD DA AB + CD DA AB BC − DA AB BC CD )
(4 AB ∧ BC ∧ CD )−1
6.4 Sea ABCD un tetraedro, y sea π un plano que corta las aristas AB , AC , DC y
DB en los puntos M, N, E y F respectivamente. Si para diferentes posiciones de π ,
MNEF es un paralelogramo, demostrar que el centro O de este paralelogramo recorre
entonces una recta fija. Demostrar también que el área máxima de este paralelogramo se
obtiene cuando M, N, E y F son los puntos medios de las respectivas aristas.