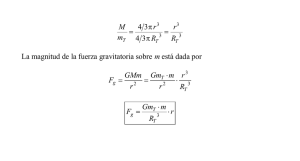
Movimiento circular y ley de gravitación universal
Anuncio

http://www.humbertomosquera.com.co Wilson, College Physics, 6th Edition Chapter 7 Movimiento circular y ley de gravedad Numbered Equations x r cos (7.1a) y r sin (7.1b) o (7.2) s r (7.3) o t t to t average angular speed or t v r (7.4) instantaneous angular speed (7.5) tangential speed relation to angular speed for circular motion (7.6) f 1 T frequency and period (7.7) 2 2 f T angular speed in terms of period and frequency (7.8) ac v2 r magnitude of cenripetal acceleration in terms of tangential speed (7.9) ac v 2 (r ) 2 r 2 r r Fc mac mv 2 r magnitude of cenripetal acceleration in terms of angular speed magnitude of centripetal force (7.10) (7.11) 1 o t or o t (constant angular acceleration) (constant angular acceleration only) v (r ) r r t t t at so at r magnitude of tangential acceleration x vt t v (7.12) v vo 2 (1) o 2 (2) o t (3) v vo at (7.13) x xo vo t 12 at 2 v 2 vo2 2a ( x xo ) o o t 12 t 2 (4) 2 o2 2 ( o ) (5) Fg Gm1m2 r2 (7.14) ag GM r2 (7.15) agE g ag GM E RE2 (7.16) GM E ( RE h) 2 (7.17) Gm1m2 r (7.18) U 2 U Gm1m2 GmM E r RE h E K U 12 m1v 2 (7.19) Gm1m2 r (7.20) U U12 U13 U 23 Gm1m2 Gm1m3 Gm2 m3 r12 r13 r23 (7.21) 4 2 3 T2 r GM s or T 2 Kr 3 (7.22) 2GM E RE vesc (7.23) vesc 2 gRE v (7.24) GM E r (7.25) E K U 12 mv 2 E K GmM E 2r GmM E r (7.26) total energy of an Earth-orbiting satellite (7.27) GmM E E 2r (7.28) 3 Chapter Review s r (7.3) t (general, not limited to constant acceleration) o 2 o t (7.5) constant acceleration only (2, Table 7.2) constant acceleration only (7.12) Con formato o o t 12 t 2 constant acceleration only (4, Table 7.2) Con formato o2 2 ( o ) constant acceleration only (5, Table 7.2) v r (7.6) f 1 T (7.7) 2 2 f T (7.8) ac v2 r 2 r (7.10) Fc mac mv 2 r (7.11) at r Fg (7.13) Gm1m2 r2 2 (G 6.67 10 11 N m 2 kg ) (7.14) 4 ag GM E ( RE h) 2 (7.17) Gm1m2 r (7.18) U T 2 Kr 3 2GM E 2 gRE RE vesc E (7.22) (7.23, 7.24) GmM E 2r (7.27) K E (7.28) 5