MATEM´ATICAS I Ia APELLIDOS: NOMBRE: 1. (0.1 ptos.) Dibuja la
Anuncio
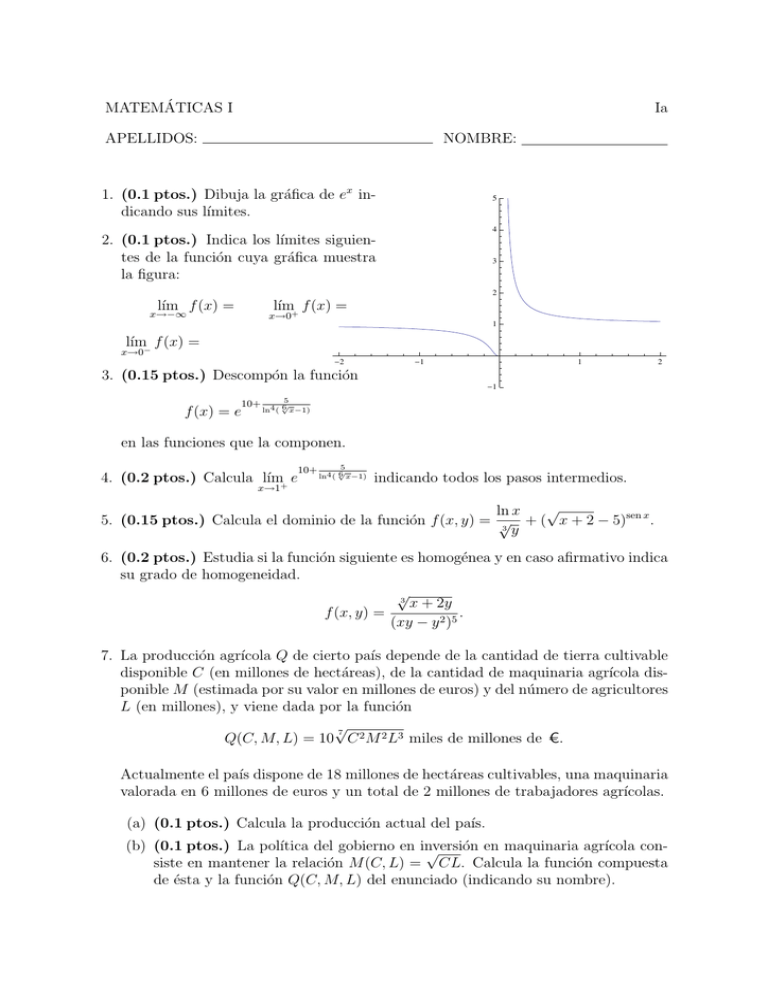
MATEMÁTICAS I Ia APELLIDOS: NOMBRE: 1. (0.1 ptos.) Dibuja la gráfica de ex indicando sus lı́mites. 5 4 2. (0.1 ptos.) Indica los lı́mites siguientes de la función cuya gráfica muestra la figura: 3 2 lı́m f (x) = lı́m+ f (x) = x→−∞ x→0 1 lı́m f (x) = x→0− !2 !1 3. (0.15 ptos.) Descompón la función 1 2 !1 5 10+ 4 √ ln ( 6 x−1) f (x) = e en las funciones que la componen. 10+ 4. (0.2 ptos.) Calcula lı́m+ e x→1 5 √ ln4 ( 6 x−1) indicando todos los pasos intermedios. √ ln x 5. (0.15 ptos.) Calcula el dominio de la función f (x, y) = √ + ( x + 2 − 5)sen x . 3 y 6. (0.2 ptos.) Estudia si la función siguiente es homogénea y en caso afirmativo indica su grado de homogeneidad. √ 3 x + 2y f (x, y) = . (xy − y 2 )5 7. La producción agrı́cola Q de cierto paı́s depende de la cantidad de tierra cultivable disponible C (en millones de hectáreas), de la cantidad de maquinaria agrı́cola disponible M (estimada por su valor en millones de euros) y del número de agricultores L (en millones), y viene dada por la función √ 7 Q(C, M, L) = 10 C 2 M 2 L3 miles de millones de C. Actualmente el paı́s dispone de 18 millones de hectáreas cultivables, una maquinaria valorada en 6 millones de euros y un total de 2 millones de trabajadores agrı́colas. (a) (0.1 ptos.) Calcula la producción actual del paı́s. (b) (0.1 ptos.) La polı́tica del gobierno en inversión en maquinaria agrı́cola con√ siste en mantener la relación M (C, L) = CL. Calcula la función compuesta de ésta y la función Q(C, M, L) del enunciado (indicando su nombre). (c) (0.2 ptos.) Explica la diferencia de interpretación entre la función Q(C, M, L) y la función compuesta calculada en el apartado anterior. (d) (0.2 ptos.) Calcula ∆Q(18, 6, 2)(−2, −1, 2) e interpreta el resultado. ¿Puede ocurrir que la producción del paı́s varı́e realmente de esta forma? (e) (0.2 ptos.) Calcula cuántos millones de trabajadores serı́an necesarios, teniendo en cuenta la polı́tica del gobierno, para que la producción agrı́cola de los 18 millones de hectáreas disponibles aumentara hasta los 80 miles de millones de C. C (f) (0.1 ptos.) La figura muestra la curva 90 de nivel de producción actual y la co- 81 72 rrespondiente a un nivel de producción 63 de 80 miles de millones de C. Razona 54 cuál es cuál y señala en ellas los puntos 45 36 correspondientes a la situación actual 27 18 y a la del apartado anterior. 9 1 (g) (0.1 ptos.) Escribe la ecuación de la curva de nivel que está más arriba en la figura e interprétala. 2 3 4 5L (h) (0.2 ptos.) Calcula la función implı́cita C(L) determinada por dicha curva de nivel. (i) (0.2 ptos.) Calcula C(2.5) e interprétalo. Comprueba que el valor que obtienes se corresponde con la gráfica. 8. (0.2 ptos.) Dadas las matrices A= 1 1 2 −1 , 1 1 1 0 B= √ 2 −1 2 3 1 1 3 0 calcula el determinante de AB y la inversa de BA ! , MATEMÁTICAS I Ib APELLIDOS: NOMBRE: 1. (0.1 ptos.) Indica los lı́mites siguientes de la función cuya gráfica muestra la figura: lı́m f (x) = x→−∞ 5 4 lı́m f (x) = 3 x→0+ 2 lı́m f (x) = x→0− 1 2. (0.15 ptos.) Descompón la función 1 √ f (x) = !2 4 (5 + e− x2 +1 )10 en las funciones que la componen. 3. (0.2 ptos.) Calcula lı́m x→−∞ (5+e− 1 √ 4 x2 +1 )10 !1 1 2 !1 indicando todos los pasos intermedios. 4. (0.1 ptos.) Dibuja la gráfica de ln x indicando sus lı́mites. 5. (0.15 ptos.) Calcula el dominio de la función f (x, y) = s (x + 1)y √ + ln(3x + 3 y). x−1 6. (0.2 ptos.) Estudia si la función siguiente es homogénea y en caso afirmativo indica su grado de homogeneidad. f (x, y) = v u u 3 t x3 . (xy + y 2 )7 7. El ahorro mensual (en euros) de un trabajador viene dado por la función s A(r, p) = 10 4 r2 , p3 donde r es su salario (en euros) y p un indicador de los precios de los bienes que consume habitualmente. Actualmente, el trabajador ahorra 180 C /mes. (a) (0.1 ptos.) Escribe la ecuación de la curva de nivel 180 de la función A e interprétala. (b) (0.2 ptos.) Calcula la función implı́cita r(p) determinada por dicha curva de nivel. r (c) (0.1 ptos.) La figura muestra las curvas de nivel correspondientes a A = 180 y A = 200. Razona cuál es cuál. 3000 (d) (0.1 ptos.) Razona a partir de la figura si, en caso de que el ı́ndice de precios fuera p = 3, el trabajador podrı́a ahorrar 200 C /mes con un salario de 1 900 C. 1000 2500 2000 1500 500 1 2 3 4 p (e) (0.2 ptos.) Calcula r(2) e interpreta el resultado. Señala en la gráfica el punto correspondiente. (f) (0.1 ptos.) Supongamos que el salario del trabajador se revisa anualmente √ teniendo en cuenta el ı́ndice de precios, según la relación r(p) = 700 p. Calcula la composición de las funciones A(r, p) y r(p). Indica el nombre de la función compuesta y simplifı́cala. (g) (0.2 ptos.) Se cumple (no hace falta que lo compruebes) que A(3) = 152.75 C. Interpreta este resultado. (h) (0.2 ptos.) Calcula ∆A(1 400, 4)(600, 5) e interpreta el resultado. ¿Podrı́a darse la situación que expresa este incremento teniendo en cuenta los apartados anteriores? (i) (0.2 ptos.) Calcula el ı́ndice de precios que permite al trabajador ahorrar 180 euros mensuales teniendo en cuenta sus condiciones salariales. 8. (0.2 ptos.) Dadas las matrices A= 1 1 2 −1 , 1 1 1 0 B= √ 2 −1 2 3 1 1 3 0 calcula el determinante de AB y la inversa de BA ! , MATEMÁTICAS I Ic APELLIDOS: NOMBRE: 1. (0.1 ptos.) Dibuja la gráfica de ex indicando sus lı́mites. 5 4 2. (0.15 ptos.) Indica los lı́mites siguientes de la función cuya gráfica muestra la figura: 3 2 lı́m f (x) = lı́m f (x) = x→−∞ x→0+ 1 lı́m f (x) = x→0− !2 !1 3. (0.2 ptos.) Descompón la función 10+ f (x) = e 1 2 !1 5 √ ln4 ( 6 x−1) en las funciones que la componen. 10+ 4. (0.2 ptos.) Calcula lı́m+ e x→1 5 √ ln4 ( 6 x−1) indicando todos los pasos intermedios. √ ln x 5. (0.2 ptos.) Calcula el dominio de la función f (x, y) = √ + ( x + 2 − 5)sen x . 3 y 6. (0.2 ptos.) Estudia si la función siguiente es homogénea y en caso afirmativo indica su grado de homogeneidad. √ 3 x + 2y f (x, y) = . (xy − y 2 )5 7. La producción agrı́cola Q de cierto paı́s depende de la cantidad de tierra cultivable disponible C (en millones de hectáreas), de la cantidad de maquinaria agrı́cola disponible M (estimada por su valor en millones de euros) y del número de agricultores L (en millones), y viene dada por la función √ 7 Q(C, M, L) = 10 C 2 M 2 L3 miles de millones de C. Actualmente el paı́s dispone de 18 millones de hectáreas cultivables, una maquinaria valorada en 6 millones de euros y un total de 2 millones de trabajadores agrı́colas. (a) (0.1 ptos.) Calcula la producción actual del paı́s. (b) (0.1 ptos.) La polı́tica del gobierno en inversión en maquinaria agrı́cola con√ siste en mantener la relación M (C, L) = CL. Calcula la función compuesta de ésta y la función Q(C, M, L) del enunciado (indicando su nombre). (c) (0.2 ptos.) Explica la diferencia de interpretación entre la función Q(C, M, L) y la función compuesta calculada en el apartado anterior. (d) (0.2 ptos.) Calcula ∆Q(18, 6, 2)(−2, −1, 2) e interpreta el resultado. ¿Puede ocurrir que la producción del paı́s varı́e realmente de esta forma? (e) (0.2 ptos.) Calcula cuántos millones de trabajadores serı́an necesarios, teniendo en cuenta la polı́tica del gobierno, para que la producción agrı́cola de los 18 millones de hectáreas disponibles aumentara hasta los 80 miles de millones de C. C (f) (0.1 ptos.) La figura muestra la curva 90 de nivel de producción actual y la co- 81 72 rrespondiente a un nivel de producción 63 de 80 miles de millones de C. Razona 54 cuál es cuál basándote en su significado 45 36 y señala en ellas los puntos correspon- 27 dientes a la situación actual y a la del 189 apartado anterior. 5L 1 2 3 4 (g) (0.15 ptos.) Escribe la ecuación de la curva de nivel que está más arriba en la figura e interprétala. (h) (0.2 ptos.) Calcula la función implı́cita C(L) determinada por dicha curva de nivel. (i) (0.2 ptos.) Calcula C(2.5) e interprétalo. Comprueba que el valor que obtienes se corresponde con la gráfica. MATEMÁTICAS I Id APELLIDOS: NOMBRE: 1. (0.15 ptos.) Indica los lı́mites siguientes de la función cuya gráfica muestra la figura: lı́m f (x) = x→−∞ 5 4 lı́m f (x) = 3 x→0+ 2 lı́m f (x) = x→0− 1 2. (0.2 ptos.) Descompón la función 1 √ f (x) = !2 4 (5 + e− x2 +1 )10 en las funciones que la componen. 3. (0.2 ptos.) Calcula lı́m x→−∞ (5+e− 1 √ 4 x2 +1 )10 !1 1 2 !1 indicando todos los pasos intermedios. 4. (0.1 ptos.) Dibuja la gráfica de ln x indicando sus lı́mites. 5. (0.2 ptos.) Calcula el dominio de la función f (x, y) = s (x + 1)y √ + ln(3x + 3 y). x−1 6. (0.2 ptos.) Estudia si la función siguiente es homogénea y en caso afirmativo indica su grado de homogeneidad. f (x, y) = v u u 3 t x3 . (xy + y 2 )7 7. El ahorro mensual (en euros) de un trabajador viene dado por la función s A(r, p) = 10 4 r2 , p3 donde r es su salario (en euros) y p un indicador de los precios de los bienes que consume habitualmente. Actualmente, el trabajador ahorra 180 C /mes. (a) (0.15 ptos.) Escribe la ecuación de la curva de nivel 180 de la función A e interprétala. (b) (0.2 ptos.) Calcula la función implı́cita r(p) determinada por dicha curva de nivel. r (c) (0.1 ptos.) La figura muestra las curvas de nivel correspondientes a A = 180 y A = 200. Razona cuál es cuál basándote en su significado. 3000 (d) (0.1 ptos.) Razona a partir de la figura si, en caso de que el ı́ndice de precios fuera p = 3, el trabajador podrı́a ahorrar 200 C /mes con un salario de 1 900 C. 1000 2500 2000 1500 500 1 2 3 4 p (e) (0.2 ptos.) Calcula r(2) e interpreta el resultado. Señala en la gráfica el punto correspondiente. (f) (0.1 ptos.) Supongamos que el salario del trabajador se revisa anualmente √ teniendo en cuenta el ı́ndice de precios, según la relación r(p) = 700 p. Calcula la composición de las funciones A(r, p) y r(p). Indica el nombre de la función compuesta y simplifı́cala. (g) (0.2 ptos.) Se cumple (no hace falta que lo compruebes) que A(3) = 152.75 C. Interpreta este resultado. (h) (0.2 ptos.) Calcula ∆A(1 400, 4)(600, 5) e interpreta el resultado. ¿Podrı́a darse la situación que expresa este incremento teniendo en cuenta los apartados anteriores? (i) (0.2 ptos.) Calcula el ı́ndice de precios que permite al trabajador ahorrar 180 euros mensuales teniendo en cuenta sus condiciones salariales. MATEMÁTICAS I IIa APELLIDOS: 1. La función NOMBRE: √ 10 + r − 2i2 D(r, i, p) = p representa la demanda de un producto en función de la renta r de los consumidores, de su precio de venta p y de un promedio i de los precios de los artı́culos de primera necesidad. Actualmente r = 5 u.m., i = 1 y p = 0.5 C . ∂D en la situación actual. ∂i (b) (0.2 ptos.) Estudia mediante la derivada oportuna si, en la situación actual, un aumento de la renta de 1 u.m. hace aumentar o disminuir la derivada considerada en el apartado anterior. (a) (0.2 ptos.) Calcula e interpreta (c) (0.2 ptos.) Calcula e interpreta la elasticidad de la demanda respecto de p en la situación actual. (d) (0.2 ptos.) Calcula dD(5, 1, 0.5) y utiliza el resultado para determinar aproximadamente el efecto sobre la demanda de una disminución de 0.01 C en el precio y un aumento de la renta de un 2%. Expresa correctamente el incremento considerado. (e) (0.1 ptos.) Calcula la dirección de máximo crecimiento de la función D en el punto (5, 1, 0.5). A partir de este punto suponemos además que el salario Ø r del consumidor se ∂r ØØ revisa anualmente según el indicador i de modo que Ø = 5. ∂i Ø1 (f) (0.2 ptos.) Explica por qué, con toda la información disponible, no es válida la conclusión del apartado (a). Calcula la derivada que nos permite concluir si un aumento de i hace aumentar o disminuir la demanda. ¿Cuál es la conclusión, la demanda aumenta o disminuye? 8 (g) (0.2 ptos.) Sabiendo que r = 5i, D calcula la función compuesta. La figura muestra la función D(i, 0.5). 6 Escribe dicha función y calcula el valor de i que hace que la demanda 4 sea máxima. 2. (0.3 ptos.) Calcula las derivadas parciales de √ f (x, y) = (x2 + x)sen y ln3 ( 3 x + 2). 2 0.0 0.5 1.0 1.5 2.0 2.5 3.0 i 3.5 3. (0.2 ptos.) Dada la función f (x, y) = 5x ey 2 +3 , calcula ∂4f . ∂x2 ∂y 2 √ 4. La función U (x, y, z) = x ln y + ln z representa la utilidad que obtiene un consumidor al adquirir tres productos en cantidades x, y y z, donde x, y, z > 1. Actualmente consume 25 unidades del primer producto y 100 del segundo, lo que le proporciona, junto con la cantidad consumida del tercero, una utilidad de 28. (a) (0.1 ptos.) Escribe la ecuación de la curva de indiferencia correspondiente al consumo actual. Interprétala. (b) (0.1 ptos.) Comprueba mediante el teorema de la función implı́cita que la ecuación anterior define a z como función implı́cita z(x, y) para consumos similares al actual. (c) (0.2 ptos.) Calcula z(25, 100) e interpreta el resultado. (d) (0.2 ptos.) Calcula la relación marginal de sustitución Ø ∂z ØØ RMS(25, 100) = − Ø ∂y Ø(25,100) derivando implı́citamente la curva de indiferencia. (e) (0.1 ptos.) Interpreta el resultado obtenido en el apartado anterior. MATEMÁTICAS I IIb APELLIDOS: NOMBRE: 1. La función B(D, p, t) determina los beneficios de una empresa en función de su demanda D, del precio p de su producto y del tiempo en años t. En la actualidad (t = 0) la demanda es de 40.24 u.p. y el precio de venta es p = 2 C. Además Ø ∂B ØØ Ø = 10, ∂D Ø(40.24,2,0) Ø ∂B ØØ Ø = ±100, ∂p Ø(40.24,2,0) Ø ∂B ØØ Ø = −0.1. ∂t Ø(40.24,2,0) Por otra parte, la demanda de la empresa viene dada por la función D(p, t) = 100 ln(20t − 3t3 + 5) . p2 (a) (0.1 ptos.) Razona el signo que cabe esperar en la derivada de B respecto de p e interpreta dicha derivada (con el signo correcto). (b) (0.2 ptos.) Razona por qué no podemos usar la derivada considerada en el apartado anterior para determinar el efecto que tendrı́a sobre el beneficio un aumento del precio de 0.05 C. Calcula el incremento de beneficio que cabe esperar realmente si se produce tal variación del precio. (c) (0.2 ptos.) Calcula dB(40.24, 2, 0) y usa el resultado para aproximar el incremento de beneficio que cabrı́a esperar dentro de tres meses (0.25 años) si, para entonces, la empresa ha reducido su precio un 5% y su demanda ha pasado a ser de 63.65 u.p. (d) (0.1 ptos.) Razona si, con los datos del enunciado, podrı́a darse la situación descrita en el apartado anterior. (e) (0.1 ptos.) Calcula la dirección de máximo crecimiento de B en el punto (40.24, 2, 0). (f) (0.2 ptos.) Calcula la elasticidad actual de la demanda respecto del precio e interprétala. ∂D (g) (0.2 ptos.) Calcula el valor de en las condiciones actuales y razona, calcu∂p lando la derivada oportuna, si dicho valor aumenta o disminuye con el tiempo. (h) (0.2 ptos.) La figura muestra la función D(2, t). Escribe dicha función y calcula el momento en que la demanda prevista tomará su valor máximo. 2. (0.25 ptos.) Calcula las derivadas parciales de 2 f (x, y) = sen2 (xy ln y ). D 80 70 60 50 0.5 1.0 1.5 2.0 t 3. La función de producción de una empresa es Q(K, L, M ) = KL ln M , donde K, L, M son las cantidades empleadas de tres factores de producción. La empresa desea alcanzar una producción de 100 unidades de producto. (a) (0.1 ptos.) Escribe la ecuación de la isocuanta de nivel 100 (curva de nivel de producción) y comprueba mediante el teorema de la función implı́cita que define a M como función implı́cita de K y L para K, L, M > 0. (b) (0.2 ptos.) Calcula M (5, 4) e interpreta el resultado. Ø ∂M ØØ (c) (0.2 ptos.) Calcula la relación de sustitución técnica RST = − deriØ ∂L Ø(5,4) vando implı́citamente la isocuanta e interpreta el resultado. √ 4. (0.2 ptos.) Dada la función f (x, y) = 113y+1 3 x2 + 1, calcula ∂5f . ∂x2 ∂y 3 5. (0.15 ptos.) Calcula Ø Ø Ø Ø Ø Ø Ø Ø Ø Ø 4 7 2 −2 ØØ 2 3 1 −2 ØØ Ø 3 5 0 −3 ØØ −2 −2 −1 5 Ø 6. (0.1 ptos.) Calcula la matriz inversa de A= √ 4 7 2 3 ! . MATEMÁTICAS I IIIa APELLIDOS: NOMBRE: 1. Un ahorrador tenı́a 900 C en su cuenta corriente en t = 0, y la derivada Am (t) del saldo de la cuenta en cada instante t (en años) durante un periodo de 3 años viene dada por Ω 1000 (1 000√− 3t) cos 2t si 0 ≤ t < 1, Am (t) 800 Am (t) = 1 000 t − 1 400 si 1 ≤ t < 3. 600 (a) (0.5 ptos.) Calcula el ahorro medio de los dos primeros años. 400 200 0.5 (b) (0.2 ptos.) Calcula el saldo de la cuenta al cabo de esos dos años. !200 !400 1.0 1.5 2.0 2.5 3.0 t (c) (0.2 ptos.) Razona a partir de la gráfica: el saldo de la cuenta al final del segundo año ¿fue mayor o menor que al principio del segundo año?, ¿fue mayor o menor que al principio del periodo? 2. (0.5 ptos.) Calcula Z +∞ −∞ e2x dx. (e2x − 1)5 3. (0.3 ptos.) Calcula la esperanza de la variable aleatoria X cuya función de densidad es x si 0 ≤ x ≤ 5, f (x) = 1 + x3 0 en otro caso. 4. (0.5 ptos.) La función C(t) representa el capital de una empresa en función del tiempo (en años) durante un periodo de dos años [0, 2], y su derivada en porcentaje ha sido √ 10 √ e 3−t . 3−t Si el capital del la empresa al cabo de 1 año era de 1 000 u.m., calcula su capital al cabo de los 2 años. 5. (0.3 ptos.) Resuelve: x + y2 + λ = 7 2x + λ = 6 λx = 0 MATEMÁTICAS I IIIb APELLIDOS: NOMBRE: 1. Un ahorrador tenı́a 900 C en su cuenta corriente en t = 0, y la derivada Am (t) del saldo de la cuenta en cada instante t (en años) durante un periodo de 3 años viene dada por Ω 1000 (1 000√− 3t) cos 2t si 0 ≤ t < 1, Am (t) 800 Am (t) = 1 000 t − 1 400 si 1 ≤ t < 3. 600 (a) (0.5 ptos.) Calcula el ahorro medio de los dos primeros años. 400 200 0.5 (b) (0.2 ptos.) Calcula el saldo de la cuenta al cabo de esos dos años. !200 !400 1.0 1.5 2.0 2.5 3.0 t (c) (0.2 ptos.) Razona a partir de la gráfica: el saldo de la cuenta al final del segundo año ¿fue mayor o menor que al principio del segundo año?, ¿fue mayor o menor que al principio del periodo? 2. (0.5 ptos.) Calcula Z 0 +∞ e−3x √ dx. 1 − e−3x 3. (0.3 ptos.) Calcula la mediana de la variable aleatoria X cuya función de densidad es x2 si 0 ≤ x ≤ 20, f (x) = 3(1 + x3 ) 0 en otro caso. 4. (0.5 ptos.) La función C(t) representa el capital de una empresa en función del tiempo (en años) durante un periodo de dos años [0, 2], y su derivada en porcentaje ha sido √ 10 √ e 3−t . 3−t Si el capital del la empresa al cabo de 1 año era de 1 000 u.m., calcula su capital al cabo de los 2 años. 5. (0.3 ptos.) Resuelve: x2 − λ = 9 x + y = 10 λ(x − y) = 0 MATEMÁTICAS I IIIc APELLIDOS: NOMBRE: 1. El coste marginal de una empresa viene dado por Cm (x) = 20 + x sen(3 + 0.2x), donde x es la cantidad producida, y los costes fijos son de 50 u.m. (a) (0.4 ptos.) Calcula la función de costes. (b) (0.2 ptos.) Si la producción actual es x = 20 u.p., calcula el coste medio de las 5 últimas unidades producidas. 2. (0.4 ptos.) Calcula Z 0 −∞ 1 1 dx 5 1 − 3x ln (1 − 3x) 3. (0.5 ptos.) Calcula Pr(X ≤ 1), donde X es la variable aleatoria dada por la función de densidad 3 x si x ≤ 0, e f (x) = 4 3 si x ≥ 0. 4(x + 1)4 4. (0.5 ptos.) La demanda diaria de un producto es de 1 000 u.m. y su precio es p = 1 C. Además, su elasticidad viene dada por E=− pe3p . e3p + 1 Calcula la demanda que cabe esperar si el precio pasa a ser p = 3 C. 5. La gráfica muestra el beneficio marginal de una empresa durante un periodo de 4 años. Razona a partir de la gráfica: 60 Bm (t) 40 20 (a) (0.1 ptos.) ¿El beneficio acumulado por la empresa al final del periodo era mayor o menor que a su inicio? 1 !20 !40 (b) (0.1 ptos.) ¿En qué momento alcanzó la empresa el máximo beneficio acumulado? 6. (0.3 ptos.) Resuelve: x+y+λ=8 x − y = 10 λ(x2 − 1) = 0 2 3 4 t


