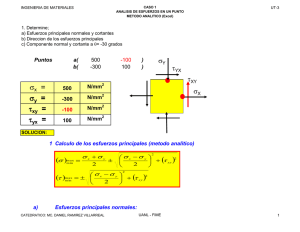
Unidad temática 3 A nálisis de esfuerzos en un punto
Anuncio

UT3 Analisis de esfuerzos en un Punto 3A Metodo Grafico 3.5 Existe una interpretación grafica de las ecuaciones anteriores hecha por el ingeniero alemán Otto Mohr (1882) a partir del uso de un círculo, por lo que se ha llamado Circulo de Mohr. Mohr. Método Grafico. Circulo de Mohr 1 MC. Daniel Ramirez Villarreal Ingenieria de los Materiales 3.5 Método grafico. Circulo de Mohr τ= σ +σ x 2 σ −σ x 2 y y + σ −σ x 2 y cos 2θ − τ sen 2θ xy 2 Ingenieria de los Materiales MC. Daniel Ramirez Villarreal Elevando al cuadrado, sumando y simplificando, Las ecuaciones (3.1) y (3.2) son las ecuaciones paramétricas de una circunferencia. Rearreglando la ecuación 3.1: σ= Método grafico. Circulo de Mohr (3.1 y 3.2) σ− σx +σ y 2 2 +τ 2 = σ x −σ y 2 2 ( )2 + τ xy (3.11) σx, σy, τxy son valores conocidos que definen el estado plano de esfuerzo, esfuerzo, mientras que σ y τ son variables. variables. sen 2θ + τ cos 2θ xy Ingenieria de los Materiales MC. Daniel Ramirez Villarreal Ingenieria de Materiales. FIME-UANL 3 MC. Daniel Ramirez Villarreal Ingenieria de los Materiales 4 MC. Daniel Ramirez Villarreal UT3 Analisis de esfuerzos en un Punto 3A Metodo Grafico Por lo tanto (σx +σy)/2 es una constante C, y el segundo miembro de la ecuació ecuación (3.11) lo consideramos como otra constante R. sustituyendo, la ecuació ecuación (3.11) se transforma en: (σ − C) + τ = R 2 2 2 Por lo que la circunferencia será de radio y centro: R= (3.12) C = Esta ecuació ecuación es aná análoga a la de una circunferencia: σx −σ 2 σx +σ 2 ( )2 + τ xy (3.13) y 2 (x(x-c)2 + y 2= R2 Ingenieria de los Materiales y 11 5 MC. Daniel Ramirez Villarreal Ingenieria de los Materiales 6 MC. Daniel Ramirez Villarreal La figura 3.5 representa el círculo de Mohr para el estado plano de esfuerzos que se ha estudiado. El centro C esta a una distancia OC del origen que es la media aritmética de los esfuerzos normales, y el radio R es la hipotenusa del triangulo rectángulo CDA. Se puede comprobar fácilmente que las coordenadas de los puntos E, F, G corresponden a las expresiones deducidas en las ecuaciones (3.5) y (3.6), por lo que el circulo de Mohr representa gráficamente la variación de los esfuerzos dada por las ecuaciones (3.1) y (3.2). Figura 3.5 Circulo de Mohr estado plano de esfuerzo bidimensional bidimensional 7 Ingenieria de los Materiales MC. Daniel Ramirez Villarreal Ingenieria de Materiales. FIME-UANL MC. Daniel Ramirez Villarreal 8 Ingenieria de los Materiales MC. Daniel Ramirez Villarreal UT3 Analisis de esfuerzos en un Punto 3A Metodo Grafico σx Dado el estado de esfuerzos biaxial: σy τ σy τyx ) τyx σx > σy, σx τxy ) b τxy ) Y b τ a σn 2 ο −σ σ σy τyx ) σ min −τ 9 Ingenieria de los Materiales MC. Daniel Ramirez Villarreal Problema propuesto (Método Gráfico Circulo de Mohr) : σx= 500 MPa τxy= 100 MPa Los esfuerzos principales normales σ1, σ2 . c) Su dirección y orientación σy = 300 MPa b a MC. Daniel Ramirez Villarreal Ingenieria de Materiales. FIME-UANL τxy= 100 MPa Y b −σ e) Su dirección y orientación Ingenieria de los Materiales σx= 500 MPa τ d) Los esfuerzos principales cortantes τ1, τ2 y σn C o σ a X −τ 11 MC. Daniel Ramirez Villarreal θ 1 c 2’ θ τ max ’ ’ +σ θ a X τ min σ max 10 MC. Daniel Ramirez Villarreal Método Gráfico: Circulo de Mohr a) Los esfuerzos componentes σx’, τxy’ para θ x’ = -30o b) θ Ingenieria de los Materiales 1. Para el estado de esfuerzos biaxial en el punto, Determinar : σy = 300 MPa 1’ Ingenieria de los Materiales 1. Identificar el estado de esfuerzos σx = + 500MPa (T) σy = - 300MPa (c) τxy = - 100MPa τyx = 100MPa 2. Hacer escala 50 MPa: 1cm. 3. Pasar los puntos a(500, -100) y b(-300, 100) a centímetros; (10,-2) y (-6, 2). 4 Trazar los ejes σ vs. τ en el papel milimétrico 5. Marcar los puntos a y b y unirlos con una línea. 6. Indicar el eje X de Ca y el y de Cb 7. Marcar el origen O y el centro C 12 MC. Daniel Ramirez Villarreal UT3 Analisis de esfuerzos en un Punto 3A Metodo Grafico τ σ n, (σ n, τ Y −σ ) τmax 1’ b (σ ,0) 2 o C (σ ,0) 1 2’ a X 9. σ −τmin ( σ n ,τ σmin 8. Con radio R = Ca = Cb trazar el circulo con centro en C. identificar los ejes principales. ,) Obtener el estado de los esfuerzos principales y sus magnitudes: midiendo en el papel milimétrico cada punto indicado en la figura a partir del origen: σ Max =(#cm)escala=518MPa(+) σ Min = #cm x (escala) = τ Max = #cm x (escala) = τ Min = #cm x (escala) = σn = #cm x (escala) = σmax −τ 13 Ingenieria de los Materiales MC. Daniel Ramirez Villarreal 11. Obtención de las orientación de los esfuerzos principales normales y cortantes. σx= 500 MPa τxy= 100 MPa σy = 300 MPa Con los ángulos anteriores se inicia la orientación con los esfuerzos principales normales, representando un sistema de ejes cartesiano X-Y , luego a partir del eje X se representa la dirección: θ1 considerando su signo y aplicando la convención; positivos en contra del reloj y negativos a favor con respecto al eje X……. ver orientación del probl. Método analítico Ingenieria de los Materiales MC. Daniel Ramirez Villarreal Ingenieria de Materiales. FIME-UANL 15 MC. Daniel Ramirez Villarreal τ (τ 10. Obtención de la dirección de los esfuerzos principales normales y cortantes σ n) Los ángulos en el circulo son el doble del valor real. 1’ Y −σ b (σ ,0) 2 2θ 1’ 1 o C 2θ 2 −τ 2’ 2θ 2’ (σ ,0) (τ , σ n) Ingenieria de los Materiales 2θ 1 a σ X 2θ Max 2θMin 2θ ’Max 2θ ’Min =+ = =+ = - θ 1 =+ #o θ 2 = - #o θ 1’ = + #o θ 2’ = - #o Ver figura 14 MC. Daniel Ramirez Villarreal 12. Obtención de las componentes de esfuerzos σx’, τxy’ para θx’=−30ο y sus correspondientes componentes a 90o ; σy’, τyx’ . θ = - 30 σx= 500 MPa Se marca en el circulo a partir τxy= 100 MPa del eje X el ángulo 2θ trazándose el nuevo eje X’ desde el centro del σy = 300 MPa circulo C y la intersección será el punto cuyas coordenadas son: σx’, τxy’ luego a 90 o de este eje se encuentra el eje Y’ en cuya intersección con el circulo representa el punto con coordenadas σy’, τyx’ . Ingenieria de los Materiales 16 MC. Daniel Ramirez Villarreal UT3 Analisis de esfuerzos en un Punto 3A Metodo Grafico o y σ y τ Calculo de: σx’ , τxy’ y’ xy’ xy’ para θ= -30 xy’ para θ’ = -30 + 90 = 60o τ σ y’ σy b a τ −σ σx τxy ) b’ y b σ y’ θ’=120ο ο 2 σy τyx ) −τ σ x’ 1 c τ xy’ xy’ a’ x’ Ingenieria de los Materiales MC. Daniel Ramirez Villarreal Ingenieria de Materiales. FIME-UANL τ yx’ yx’ θ=− θ=−60ο a +σ x 5A-P 17 MC. Daniel Ramirez Villarreal