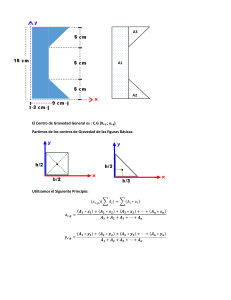
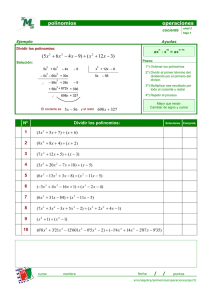
EJERCICIO de PRIMITIVAS CON COCIENTE DE POLINOMIOS
Anuncio

EJERCICIO de PRIMITIVAS CON COCIENTE DE POLINOMIOS CUYO DENOMINADOR TIENE RAICES MULTIPLES (HECHO EN CLASE 2ºINT) 7 1 8 2 Para calcular esta primitiva, previamente hay que descomponer el cociente de polinomios en fracciones más simples. = Y ahora haciendo “común denominador”, queda: 7 8 1 + . . 1 2 + . 1 2 + . 2 Esta última igualdad queremos que sea una identidad. Entonces se tiene que cumplir ∀x, x∈\. Con la finalidad de calcular los coeficientes a, b, c y d, vamos a darle a x valores convenientes. Como tenemos 4 incógnitas, necesitamos 4 ecuaciones independientes. Podríamos utilizar 4 valores cualesquiera, pero será más fácil si utilizamos los valores que anulan algunos factores. Veámoslo. 7 Si x=2, 7. 3 8 . 1 + . 1 2 + . 1 2 + . 2 8 . 1 + . 1 2 + . 1 2 + . 2 8 . 1 + . 1 2 + . 1 2 + . 2 15 . 22 Si x=1, 7. 1 15 Ahora utilizamos cualquier valor para x. Por ejemplo, 0 y 3. Si x=3, Si x=0, 7. 7. 8 . 29 8 8 . 8 1 + . 4 1 2 + . 1 2 + . 2 1 2 + . 1 2 + . 2 2 1 + . 2 2 2 Resolviendo el sistema de las dos últimas ecuaciones, se obtiene 22 y 22. Entonces: 7 1 7 1 8 2 2 8 22 2 2 1 22 1 1 1 22 1 15 1 Para terminar, la respuesta final es: 22 ln| 2| 22 ln| 1| ∈\ , + Las primitivas que utilizamos para resolver este ejercicio son: 1 1 1 | | 7 1 | 1 7| 1 6 1 1 2 6 1 1 2 1 1 1 Se agradece al estudiante Claudio Díaz del 2ºI del Profesorado de Informática por su colaboración en la realización de este ejercicio.