Campo Eléctrico - IES Francisco Grande Covián

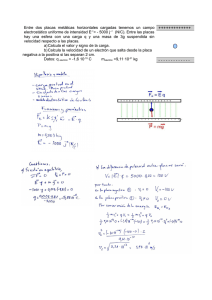
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
1
= 9 ⋅ 10 9 N m 2 C − 2
4πε 0
Zaragoza Septiembre 97; 3,6 10 –3 J
K=
Campo Eléctrico
1.- Nuestra experiencia se va a desarrollar en
una región del espacio en donde existe un campo
eléctrico uniforme. Una partícula de masa m y
carga q se deposita sin velocidad inicial en un
punto en donde el potencial vale V 1 .
a) Calcula la velocidad de la partícula cuando pase por otro punto cuyo potencial sea V 2
b) Si el campo eléctrico no fuera uniforme, pero
los valores de V 1 y V 2 , fueran los mismos, ¿sería
diferente la respuesta del apartado anterior? Razona la contestación. Zaragoza Septiembre 96
2.- Una partícula de masa m = 1 g y con carga
q= – 1 μC describe una órbita circular de radio R
= 1 cm en tomo a otra partícula fija con carga q' =
5 μC. La interacción gravitatoria entre ambas es
despreciable. La constante de Coulomb es
1
K=
= 9 ⋅ 10 9 N m 2 C − 2
4πε 0
Calcula la velocidad orbital de la primera partícula y su energía mecánica. Zaragoza Junio 97
3.- a) Explica el concepto de energía potencial
eléctrica. ¿Qué energía potencial eléctrica tiene
una carga q 1 situada a una distancia r de otra q 2?
b) Dos partículas con igual carga q = 0,1 μC están
fijas en el vacío y separadas una distancia d = 1
m. Otra partícula de carga q' = 2 μC, sobre la que
sólo actúa el campo eléctrico de las anteriores. se
desplaza desde el punto A hasta el B de la figura,
situados en el punto medio entre las dos cargas y
en el punto que forma un triángulo equilátero con
ambas, respectivamente. En el desplazamiento A---->B, ¿cuánto variará la energía cinética de q'?
Constante de Coulomb:
D:\2ºbachiller\caelectrico\caele09.doc
4.- Una partícula de carga 6 10 –6 C se encuentra en reposo en el punto (0, 0). Se aplica un campo eléctrico uniforme de 500 N C –1 dirigido en
sentido positivo del eje OY.
a) Describe la trayectoria seguida por la partícula
hasta el instante en que se encuentra en el punto
A, situado a 2 m del origen. ¿Aumenta o disminuye la energía potencial de la partícula en dicho
desplazamiento? ¿En qué se convierte dicha variación de energía?
b) Calcula el trabajo realizado por el campo en el
desplazamiento de partícula y la diferencia de potencial entre el origen y el punto A. Andalucía 98.
Igual dirección y sentido que el campo; M.R.U.A.;
Disminuye Ep; se convierte en Ec; 6 10 –3 J
5.- Una placa conductora cargada positivamente crea en sus proximidades un campo eléctrico
uniforme E = 1000 V/m. tal y como se indica en la
figura. Desde un punto de la placa se lanza un
electrón con velocidad v = 10 7 m/s formando un
ángulo α
= 60º con
dicha
placa, de
forma
que el
electrón
describirá una
trayectoria como la indicada en la figura.
a) En el punto A, el más alejado de la placa, ¿con
qué velocidad se mueve el electrón? Respecto al
punto inicial, ¿cuánto ha variado su energía potencial electrostática? Calcula la distancia d entre
el punto A y la placa.
b) Determina la velocidad (módulo y orientación)
del electrón cuando choca con la placa (punto B).
Datos: e = 1,6.10 –19 C, m e = 9,1 10 –31 kg.
Zaragoza Septiembre 98
r
r
5,0 ⋅10 6 i + 0 j m / s ; +3,42 10 –17 J ; 0,21 m;3,36
r
r
10 –17 J; 10 7 cos 60i + 10 7 sen 60 (− j ) m / s S
6.- Tenemos dos cargas eléctricas puntuales de
2 C y –5 C, separadas una distancia de 10 cm.
Calcula el campo en los puntos siguientes:
a) A 20 cm de la carga positiva, tomados en la dirección de la recta que une las cargas y en el sentido de la negativa a la positiva.
b) A 20 cm de la carga negativa, contados en la
misma dirección pero en el sentido de la positiva a
la negativa.
c) ¿En qué punto de dicha recta es nulo el potencial eléctrico? Baleares98.
Luis Ortiz de Orruño
pg 1 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
I.E.S. Francisco Grande Covián
Campo Eléctrico
mailto:lortizdeo@hotmail.com
26 de septiembre de 2009
Física 2ªBachiller
r
r
r
r
Datos: Constante de la ley de Coulomb K = 9 10 9
E = 5 ⋅1010 i NC −1 ; E = −92,5 ⋅1010 i NC −1 ; 0,029
N m 2 C -2 Madrid 97; 1,7 10 –7 C ; 4 m ; +0,21 J
a dcha+ y 0,067 a izda –
11.- ¿Puede existir diferencia de potencial eléc7.- La separación entre dos placas verticales
trico entre dos puntos de una región en la cual la
metálicas cargadas, una positivamente y otra neintensidad del campo eléctrico es nula? ¿Qué relagativamente, es de 15 cm en el vacío. El campo
ción general existe entre el vector intensidad de
eléctrico entre las placas es uniforme y de módulo
campo eléctrico y el potencial eléctrico? Razona
3000 N/C. Un electrón se deja libre desde el relas respuestas. Madrid 97
poso en un punto P sobre la superficie de la placa
negativa. Determinar:
12.- Se tienen dos cargas eléctricas de 3 μC cada
a) La velocidad que llevará en el momento de couna, una positiva en el origen de coordenadas y la
lisionar, en un punto A, con la otra placa y la pootra negativa, a una distancia de 20 cm. En el sensición de dicho punto A con respecto al P .
tido positivo del eje de las X. Calcular la intensib) Supongamos que el electrón se lanza desde P
dad del campo eléctrico y el potencial eléctrico en
verticalmente hacia arriba con una velocidad de 5
los siguientes puntos:
10 6 m/s. A qué distancia del punto A, sobre la
a) En el punto medio del segmento que las une.
placa, golpea el electrón? ¿Por encima o por debab) En un punto equidistante 20 cm de ambas carjo de A?
gas.
Carga del electrón = 1,602 10 –19 C, masa del elecDatos. Medio en el vacío.
trón: 9,1 10 –31 kg.. Desprecie la fuerza de la graConstante de la ley de Coulomb, K= 9 10 9 N m 2
vedad.
C –2
7
Baleares Junio 1996. 1,26 10 m/s encima 0,12 m
Madrid. Junio, 1996
r
r N
r N
8.- En una región de espacio existe un campo
ET = 5,4 ⋅10 6 i
; 0V; 6,75 ⋅10 5 i
;0V S
C
C
eléctrico uniforme E = 1000 N/C. En un punto P
de esta región, donde supondremos que el poten13.- En la figura se representan algunas superficial eléctrico es nulo, V(P) = 0 , liberamos un
cies correspondientes
protón con velocidad inicial nula.
a una zona del espaCalcula su energía potencial y su velocidad cuancio donde existe un
do haya recorrido una distancia d = 10 cm.
campo electrostático.
–19
–27
Datos: e = 1,6.10 C, m p = 1.7 10 kg .
a) ¿Qué dirección y
Zaragoza Septiembre 98
sentido tendrán las
líneas de campo del
9.- Cuatro cargas, q 1 = 2 μC, q 2 = -3μC, q 3 = -4
citado campo eléctriμC y q 4 = 2 μC,
están situadas en
los vértices de
un rectángulo,
co?
como indica la
b) Si en el instante de tiempo
figura adjunta.
t = 0 situamos un electrón en
Halla la fuerza
el punto A y desde el reposo
total que ejercen
se deja en libertad, ¿cuáles
las cargas q l , q 2
serán la dirección y el sentiy q 3 sobre q 4 .
do de la trayectoria inicial
Dato: K = 9 10 9 unidades SI. Canarias 98
del mismo?
r
r
r
r
r
F1 = 2,25 ⋅10 −3 i ; F2 = −1,73 ⋅10 −3 i + 1,29 ⋅10 −3 j ;
c) Una carga eléctrica, ¿se
r
r
moverá siempre a lo largo de
−3
F3 = 8 ⋅10 j
una línea de campo? Justifir
r
r
Ftotal = 0,52 ⋅10 −3 i + 9,29 ⋅10 −3 j N
ca la respuesta. Cantabria 98
10.- A una distancia "r" de una carga puntual
"Q", fija en un punto O, el potencial eléctrico es V
= 400 V y la intensidad de campo eléctrico es E =
100 N/C. Si el medio considerado es el vacío, determinar:
a) Los valores de la carga "Q" y de la distancia "r"
b) El trabajo realizado por la fuerza del campo al
desplazarse una carga de 1 mC, desde la posición
que dista de O el valor "r" calculado, hasta una
posición que diste de O el doble de la distancia
anterior.
D:\2ºbachiller\caelectrico\caele09.doc
14.- En una región del espacio (0 ≤ x ≤ 1m ) existe un campo eléctrico. Sabiendo que el potencial
Luis Ortiz de Orruño
pg 2 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
eléctrico solamente varía a lo largo del eje X tal y
como se muestra en la figura. Se pide:
a) ¿Cuánto vale el campo eléctrico en dicha región?
b) ¿Qué trabajo realizará el campo eléctrico para
trasladar una carga eléctrica q = 0,1 10 -6 C desde
el punto (x 1 ,y 1 ) = (0,1, 0,3) hasta (x 2 ,y 2 )= (0,5,
0,8)? ¿Y si el punto final fuera (x 3 ,y 3 ) = (0,5, l)?
r
(Unidades en metros.) Cantabria 98. 20i NC –1 ; 8 10 –7 J
15.- Dos cargas positivas de 5 μC cada una, situadas en el eje de las X, una en el origen y la otra
a 10 cm en el sentido positivo del eje X
a) calcular el campo eléctrico en módulo, dirección y sentido, en x= 2 cm
b) calcular el potencial eléctrico en x = 15 cm
b) ¿En qué punto del eje de las X el campo es cero?
1
Datos: K =
= 9 ⋅ 10 9 N m 2 C − 2
4πε 0
r
r
105,47 i N / C ; 20 ⋅10 6 i N / C S
16.- Ley de Coulomb de la interacción electrostática. Explica el significado de cada una de las
magnitudes que intervienen en la expresión vectorial de la ley.
Canarias 98
17.- Si una carga eléctrica negativa se desplaza
en un campo eléctrico uniforme a lo largo de una
línea de fuerza bajo la acción de la fuerza del
campo:
a) ¿Cómo varía la energía potencial de la carga al
pasar ésta desde un punto A a un punto B del
campo?
b) ¿Dónde será mayor el potencial eléctrico del
campo en A o en B?
Razona las respuestas. Madrid 97
r
18.- Un electrón entra con velocidad v 0 =8 10 5
m/s en una zona del espacio donde hay un campo
r
eléctrico E =10 N/C vertical creado por las armaduras de un condensador, la distancia d vale 10
cm
D:\2ºbachiller\caelectrico\caele09.doc
la baldufa
http://baldufa.upc.es/index.htm
19.- Una vez que el electrón entra en el condensador:
a) Dibujar las fuerzas actúan sobre el electrón.
Hacer un cálculo e indicar si son despreciables los
efectos de la gravedad.
b) ¿Qué movimiento describirá el electrón. Describir su trayectoria, tomando como origen de coordenadas el punto A de entrada del electrón en el
condensador.
c) ¿Qué tiempo emplea el electrón en salir del espacio interior del condensador?
d) ¿Cuáles son las coordenadas x e y del punto de
salida?
q(electrón) = 1,6 10 -19 C ; masa(electrón) = 9,11
10 -31 kg .
Cataluña Septiembre 97; Si Felec/Fgrav=1,80
10 11 ; y = 1,37 x 2 ; 1,25 10 –7 s ; (0,1,0,0137) m
20.- Enuncia y comenta la expresión de la fuerza
de Coulomb entre cargas eléctricas en reposo. Asturias 2003
21.- Consideramos las superficies equipotenciales producidas por una carga puntual de valor q =
2 10 –6 C colocada en el origen de coordenadas.
a) Haz un esquema de las superficies equipotenciales.
b) Calcula la separación entre la superficie equipotencial de 6000 V y la de 2000 V.
e) Calcula el trabajo que tiene que realizar un
agente externo para mover una carga de prueba q 0
= 1,5 10 –3 C desde la superficie equipotencial de
6000 V hasta la de 2000 V sin variar su energía
cinética. Castilla la Mancha 98. 6 m ; 6 J.
22.- Dos cargas puntuales de 8 μC y –5 μC están
situadas, respectivamente, en los puntos (0, 0) y
(1, l). Calcula:
a) La fuerza que actúa sobre una tercera carga de
1 μC situada en el punto(2,2).
b) El trabajo necesario para llevar esta última carga desde el punto que ocupa hasta el punto (0, l).
Datos: K = 9,00 10 9 N. m 2 C –2 . Las coordenadas
Luis Ortiz de Orruño
pg 3 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
se dan en metros. Galicia 98. :
r
r
r
F = 0,0135 cos 45 − i + sen 45 − j ; 0,033 J S
(
( )
( ))
23.- Una esferita de 10 gramos de masa cuelga
de un hilo sujeto a la placa
superior como
se indica en la
figura. Si la
distancia entre las placas
es de 5 cm y
la diferencia de potencial es de 10 3 V.
a) Dibuja la dirección y sentido del campo eléctrico y calcula su módulo.
b) ¿Cuál es el signo y el valor de la carga eléctrica
que debe tener la esfera para que la tensión del
hilo sea nula? 2 10 4 N/C vertical hacia abajo 4,9
10 –6 C negativa S
24.- Supón que junto a la superficie de la Tierra
existe, además de su campo gravitatorio g = 10
N/kg un campo eléctrico uniforme dirigido en
vertical y hacia arriba E = 10 4 N/C. En esta región
soltamos una partícula de masa m = 0,01 kg. con
velocidad inicial nula.
a) Cuál debe ser su carga para que permanezca en
reposo?
b) Si la carga de la partícula es el doble de la que
acabas de calcular, realizará un movimiento ascendente. ¿Por qué? Calcula su velocidad cuando
haya ascendido 2 m respecto al punto inicial. Zaragoza Junio 97
positiva, 1 10 –5 C ; 6,3 m/s S
25.- Una carga puntual de –5 10 –6 C está localizada en el punto de coordenadas x = 4 m, y =–2
m. Una segunda carga puntual de 12 10 –6 C está
localizada en x = 1 m, y = 2 m.
a) Determina la magnitud y la dirección del campo
eléctrico en x=– 1 m y =0.
b) Calcula el potencial en el mismo punto del
apartado anterior. La Rioja 98.
r
r
r
E = −8105,19i − 10122,2 j N / C ; 29828 V
26.- Una pequeña esfera de 0,2 g cuelga de un
hilo de masa despreciable entre dos láminas verticales paralelas separadas 5 cm. La esfera tiene una
carga positiva de 6 10 –9 C.
a) ¿Qué diferencia de potencial entre las láminas
hará que el hilo forme un ángulo de 45º con la
vertical?
b) ¿Cuál será la intensidad del campo eléctrico entre las láminas?
c) Representa gráficamente las fuerzas que actúan
sobre la carga en la posición de equilibrio. País
Vasco 98. 1,6 10 4 V , 3,3 10 5 NC –1
27.- Dos partículas con cargas q 1 = 1 μC y q 2 =
2 μC están separadas una distancia d = 0,5 m.
a) Calcula la fuerza que actúa sobre la segunda y
su energía potencial electrostática.
D:\2ºbachiller\caelectrico\caele09.doc
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
b) Si q 2 puede moverse, partiendo del reposo,
¿hacia dónde lo hará? Calcula su energía cinética
cuando se haya desplazado 0,2 m respecto a su
posición inicial. ¿Cuánto trabajo habrá realizado
hasta entonces el campo eléctrico? Constante de
Coulomb: K =9 10 9 N.m 2 .C –2 . Zaragoza 98. 0,072
N de repulsión; 0,036 J ; 0,011 J ; 0,011J; hacia
pot decre. S
28.- Se tienen dos iones con carga 2 e y – e
separados una distancia de 3Å. Calcula:
a) Distancia del ion positivo a la que se anula el
campo eléctrico total.
b) Distancia del ion positivo a la que se anula el
potencial eléctrico total a lo largo del tramo recto
comprendido entre los dos iones.
c) Energía potencial eléctrica de los dos iones.
1
Datos:
= 9 ⋅10 9 Nm 2 C − 2 ; e = 1,6 10 -19 C.
4πε 0
Murcia 98. 10,24 10 –10 m ; 2 10 –10 y 6 10 –10 m ; –
1,54 10 –18 J
29.- Si el potencial eléctrico V es constante en
toda una región del espacio, ¿cómo es el campo
eléctrico en toda esa región? ¿Qué relación general existe entre el vector intensidad de campo
eléctrico y el potencial eléctrico? Razona las respuestas. Baleares. Junio, 1996
30.- Se sitúa en el origen de coordenadas del espacio tridimensional vacío un cuerpo puntual de
masa 10 kg y con una carga eléctrica -1 nC. En el
punto (1 m, 1 m, 1 m) se sitúa otro cuerpo puntual
de masa 20 kg y carga eléctrica - 100 pC. Determina:
a) La fuerza total que ejerce el primer cuerpo sobre el segundo.
b) ¿Cuál es el cociente entre la fuerza eléctrica y
la gravitatoria en este caso.
c) Si se separan las cargas a una distancia de 10 m
en la misma línea que antes, ¿el cociente entre las
fuerzas gravitatoria y eléctrica crece, decrece o se
mantiene?
Datos: ε 0 = 8,854 10 -12 C 2 m –2 N -1 , G = 6,67 l0 -11
r
r r r
N m 2 kg –2 Oviedo 98 Felec = 3 ⋅10 −10 i + j + k ;
r
r r r
Fgra v = 2,56 ⋅10 −9 − i − j − k ;
Luis Ortiz de Orruño
(
)
(
)
pg 4 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
I.E.S. Francisco Grande Covián
Campo Eléctrico
mailto:lortizdeo@hotmail.com
26 de septiembre de 2009
Física 2ªBachiller
r
r r r
35.- a) Escribe y comenta la ley de Coulomb (1
Ftotal = 2,39 ⋅10 −9 − i − j − k ; 0,0675 ; se mantiene
p.)
cte
b) Tres cargas puntuales q 1 = q 2 = 1μC y q3 = -1 μ C
31.- Dos pequeñas esferas iguales, de 5 N de peestán situadas en los
so cada una, cuelgan de un mismo punto fijo mevértices de un triándiante dos hilos idénticos, de 10 cm. de longitud y
gulo equilátero de
de masa despreciable. Si se suministra a cada una
lado L = 10 cm. Calde estas esferas una carga eléctrica positiva de
cula la fuerza elécigual cuantía se separan de manera que los hilos
trica (módulo y
forman entre si un ángulo de 60º en la posición de
orientación) que acequilibrio. Calcular:
túa sobre cada una
a) la tensión en el hilo.
de ellas. (1,5 p.).
b) El valor de la fuerza electrostática ejercida enConstante de Coutre las cargas de las esferas en la posición de equilomb: K = 1/(4πε 0 )=
librio.
9 10 9 N m 2 C –2
c) El valor de la carga de las esferas.
Zaragoza Septiembre 99
Datos: Constante de la ley de Coulomb K =
36.- Una carga puntual de 10 –9 C está situada en
9.10 9 N.m 2 .C -2 Madrid 97 S
el origen de coordenadas de un sistema cartesiano.
32.- En un punto situado a una distancia d de
Otra carga puntual de 20 10 –9 C está situada en el
una carga puntual fija q, medimos un potencial de
eje OY a 3 m del origen. Calcula:
500 V (con referencia en ∝) y un campo eléctrico
a) El valor del potencial electrostático en un punto
de intensidad 100 N/C. La constante de Coulomb
A situado en el eje OX a 4 m del origen.
1
b) La intensidad del campo eléctrico en dicho
9
2
−2
K=
= 9 ⋅ 10 N m C
punto.
4πε 0
es
c) El trabajo realizado para llevar una carga de 1
a) Determina los valores de la carga, q, y de la
C desde el punto A a otro B de coordenadas (4,3).
distancia, d.
(3 pto)
r
r
b) Cuánto trabajo tendríamos que realizar para
38,25 V ; 6,32i − 4,32 j N / C ; –8,55 J
trasladar, con velocidad constante. otra carga
(
)
idéntica desde el infinito hasta ese punto? Zaragoza Septiembre 97
5m; 2,8 10 –7 C ; –1,4 10 –4 J
33.- a) Explica el concepto de potencial eléctrico ¿Qué potencial eléctrico crea una carga puntual? Dibuja sus superficies equipotenciales. (1 p.)
b) Considera dos cargas puntuales fijas q 1 = 1 μC
y q 2 =–2 μC separadas una distancia L = 30 cm.
Determina la distancia a q 1 del punto sobre la recta que une ambas cargas donde el potencial eléctrico es nulo. ¿Es también nulo allí el campo eléctrico? (1,5 p.)
Zaragoza Junio 99; 0,1 m a la dcha de q 1
34.- Un electrón con energía cinética inicial
100 eV penetra en la región sombreada de la figura, de anchura d = 10 cm, donde se sabe que existe
un campo eléctrico uniforme. Se observa que el
electrón atraviesa dicha región sin desviarse de su
trayectoria rectilínea inicial, pero su velocidad a
la salida es la mitad de la inicial. Calcula:
a) La velocidad inicial v. del electrón. (1 p.)
b) El módulo y
orientación del
campo eléctrico
dentro de esa región. (1 p.)
e = 1,6 10 -19 C ;
me = 9,1 10 -31 kg.
Zaragoza Junio 99 S
D:\2ºbachiller\caelectrico\caele09.doc
37.- Dos cargas en reposo de 4 μC y 2 μC están
situadas, la primera en el origen de coordenadas, y
la segunda, a 200 cm de la primera, sobre el semieje positivo de eje OX. Calcula:
a) La intensidad del campo eléctrico en el punto
de coordenadas (1, 1) en el vacío (las coordenadas
están dadas en metros).
b) el potencial en dicho punto
c) El trabajo realizado para llevar una carga de –5
mC desde el punto (1,1) al (–3,5)
r
r
6364i + 19092 j N / C ; 38184 V; –147,3 J S
38.- Dadas dos cargas de –30 μC en (0,-1) y 20
μC en (0,2). Calcular, en la línea recta que une los
dos puntos, la posición de un punto P en el que:
a) La intensidad de campo sea cero.
b) El potencial sea cero. (0;15,35) ; S
Para visualizar líneas de campo eléctrico en:
Luis Ortiz de Orruño
pg 5 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
http://www.sc.ehu.es/sbweb/fisica/elecmagnet/ele
ctrico/cElectrico.html
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
ield/EField.html
39.- Entre las placas de un condensador plano
que están separadas 4 cm hay una partícula cargada de m = 5 miligramos y q = –3 μC. Si entre las
placas del condensador se establece una diferencia
de potencial de 240 V, calcula, sin tener en cuenta
los efectos de la gravedad:
a) La aceleración de la partícula.
b) La energía necesaria para llevar a la partícula
desde la placa positiva a la negativa. 36000 m/s 2 ;
+7,2 10 –4 J
40.- La figura representa las superficies equipotenciales de una zona del espacio donde existe un
campo eléctrico. Las superfícies están separadas
una de otra una distancia de 10 cm:
a) ¿Cuánto vale el campo eléctrico en dicha zona
del espacio?
b) Dibuja las líneas del campo eléctrico.
c) ¿Qué trabajo hay que realizar para trasladar un
electrón desde el punto 1 al punto 2? ¿Lo efectuará el propio campo eléctrico o deberemos aplicar
alguna fuerza externa? Dato: q e = –1,6 10 -19 C
Cantabria 99; 100 V/m; perpendiculares a las
sup. Equipotenciales, hacia pot decrecientes,
igualmente espaciadas; –64 10 –19 J Debemos aplicar fuerza externa.
41.- Dos esferas puntuales iguales están suspendidas, mediante hilos inextensibles y sin peso, de
un metro de longitud cada uno, de un mismo punto. Determina la carga eléctrica que han de poseer
cada una de ellas para que el hilo forme un ángulo
de 30º con la vertical.
Datos: masa de cada esfera, m = 10 g
K=9 10 9 N m 2 C -2 ; g=9,8 m s -2 Castilla-La Mancha
99; 2,5 10 –6 C
42.- Sea un campo eléctrico uniforme dado por
r
r
E = 500 i N / C . Se pide.
a) ¿Cómo serán las superficies equipotenciales en
dicho campo?
b) Calcula el trabajo necesario para trasladar una
carga de 2 μC desde el punto P (2, 3, 0) m hasta el
punto Q (6, 5, 0) m.
c) Calcula la distancia entre las superficies equipotenciales V 1 = 10 V y V 2 = 20 V. Comunidad
Valenciana 99
http://www.cco.caltech.edu/~phys1/java/phys1/EF
D:\2ºbachiller\caelectrico\caele09.doc
43.- Se libera desde el reposo un protón en un
campo eléctrico uniforme de intensidad 7 10 4 Vm –
1
dirigido a lo largo del eje X en sentido positivo.
El protón se desplaza una distancia de 0,2 m en la
dirección del campo. Calcula:
a) La diferencia de potencial que ha experimentado el protón en el desplazamiento indicado.
b) La variación de energía potencial.
c) La velocidad del protón al final de los 0,2 m recorridos.
Datos: Carga del protón 1,6 10 -19 C; Masa del
protón 1,67 10 -27 kg Extremadura 99
44.- Cuatro cargas eléctricas de 10,0 nC, -12,0
nC, 20,0 nC y 25,0 nC están colocadas en los vértices de un cuadrado de lado l = 1,2 m.
Encuentra el potencial eléctrico en el centro del
cuadrado.
Dato: Constante de Coulomb = 8,99 10 9 N m 2 C –2
Baleares 99
45.- Compara el papel que ocupa la masa en la
ley de la gravitación universal con la que ocupa la
carga en la ley de Coulomb. .¿En qué son semejantes y en qué diferentes? La Rioja 99
46.- ¿Cómo es el campo eléctrico en el interior
de una esfera metálica cargada? ¿Y el potencial?
Murcia 99
47.- En el espacio comprendido entre dos láminas planas y paralelas con cargas iguales y opuestas existe un campo eléctrico uniforme. Un electrón abandonado en reposo sobre la lámina cargada negativamente llega a la superficie de la lámina
opuesta, situada a 2 cm de distancia de la primera,
al cabo de 1,5 10 –8 s
Despreciando los efectos gravitatorios, calcula:
a) La intensidad del campo eléctrico entre las láminas.
b) La velocidad con que llega el electrón a la segunda lámina.
c) La diferencia de potencial entre las láminas.
Datos: Carga e 1,6 10 -19 C ; Masa del electrón:
me =9,10 10 –31 kg. País Vasco 99
Luis Ortiz de Orruño
pg 6 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
48.- a) Explica el concepto de energía potencial
eléctrica. ¿Qué energía potencial eléctrica tiene
una partícula de carga q 2 situada a una distancia r
de otra de carga q l? (1,5 p.)
b) Una partícula de carga q 1 = 0,1 μC está fija en
el vacío. Se sitúa una segunda partícula de carga
q 2 = 0,5 μC y masa m = 0,1 g a una distancia r =
10 cm de la primera. Si se suelta q 2 con velocidad
inicial nula, se moverá alejándose de q l . ¿Por qué?
Calcula su velocidad cuando pasa por un punto a
una distancia 3r de q l . (1,5 p.)
Constante de Coulomb: K
= l/(4 π 0 ) = 9 10 9 N m 2 C –2 .
Zaragoza Junio 2000; 7,75
m/s
49.- a) Explica el concepto de campo eléctrico.
¿Qué campo eléctrico crea
una carga puntual? (1 p.)
b) Tres partículas con cargas iguales q =1μC están
situadas en tres de los vértices de un cuadrado de
lado L = 10 cm. Calcula el campo eléctrico (módulo, dirección y sentido) en el vértice vacante, A.
(1,5 p.)
c) ¿Qué fuerza eléctrica actuaría sobre una carga
q' = -2 μC situada en este último punto? (0,5 p.)
1
= 9 ⋅ 109 Nm 2C − 2 Zaragoza Septiembre 2000
4πε 0
50.- En las proximidades de la superficie terrestre se aplica un campo eléctrico uniforme. Se observa que al soltar una partícula de 2 g cargada
con 510 –5 C permanece en reposo.
a) Determina razonadamente las características del
campo eléctrico (módulo, dirección y sentido).
b) Explica qué ocurriría si la carga fuera: i) 10 10 –
5
C ii) -5 10 –5 C Andalucía 2000; 392 N; Sube;
Baja.
51.- En una posición del espacio A, donde existe
un campo eléctrico uniforme dirigido a lo largo
del eje Z positivo, se coloca una partícula cargada
de carga q = 10 –6 C y masa m = 10 –6 kg con velocidad inicial nula.
Debido a la acción del campo eléctrico, esta partícula se acelerará hasta,, otra posición B donde llega con una velocidad cuyo módulo es 100 m/s tras
recorrer 1 m. Se pide:
a) ¿Cuál es la dirección y sentido de la velocidad
b) Dibuja las superficies equipotenciales de ese
campo eléctrico
c)¿Cuánto valdrá la diferencia de potencial entre
los dos puntos A y B
d) ¿Cuánto vale el campo eléctrico (dirección
módulo y sentido)
Nota: Desprecia la fuerza de la gravedad. Cantabria 2000; de A a B; VA–VB = 5000 V; supuesto
r
r
cte E = 5000 k
D:\2ºbachiller\caelectrico\caele09.doc
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
52.- Una carga eléctrica de 4 C es llevada desde
un punto, donde existe un potencial de 15 V, a
otro punto cuyo potencial es de 40 V. Indica sí
gana o pierde energía, y cuánta. Castilla La Mancha 2000;
53.- En los puntos A (4, 0), B (0, -4), C (-2, 0) y
D (2, 0) de un sistema de coordenadas expresadas
en metros, se encuentran, respectivamente, las
cargas eléctricas q 1 = 14 10 –5 C, q 2 = 23 10 –5 C, q 3
= –8 10 –5 C y q 4 = -6 10 –5 C. Calcula:
a) La intensidad del campo eléctrico en el punto
(0, 0).
b) El potencial eléctrico en el punto (0, 0).
c) La energía potencial eléctrica que adquiere una
carga de +25 10 –6 C al situarse en ese punto.
Datos k = 9 10 9 N m 2 /C 2 Castilla-La Mancha
r
r
2000; − 123750 i + 129375 j ; 202500 V; –5,1 J
54.- En tres vértices de un cuadrado de 2 m de
lado se disponen cargas de +10 μC. Calcula:
a) El vector intensidad de campo eléctrico en el
cuarto vértice.
b) El potencial eléctrico en dicho vértice.
c) El trabajo necesario para llevar una carga de
-5μ C desde el centro del cuadrado hasta el cuarto
vértice.
Dato: K = 9 10 9 N.m 2 C -2 Islas Canarias 2000
55.- Si un electrón se mueve en la misma dirección y sentido que las líneas de un campo eléctrico uniforme, su, energía potencial ¿aumentará,
disminuirá o permanecerá constante? ¿Y si se
mueve en la dirección perpendicular a las líneas
del campo eléctrico?. Justifica ambas respuestas
Islas Canarias 2000
56.- Dos cargas puntuales e iguales, de valor 2
μC cada una, se encuentran situadas en el plano
XY en los puntos (0, 5) y (0, -5), respectivamente,
estando las distancias expresadas en metros.
a) ¿En qué punto del plano el campo eléctrico es
nulo?
b) ¿Cuál es el trabajo necesario para llevar una
carga unidad desde el punto (1, 0) al punto (-1, 0)
Madrid 2000
57.- a) ¿Qué es una línea de campo eléctrico?
¿Qué es una superficie equipotencial?
b) ¿Qué importante relación geométrica existe entre las superficies equipotenciales y las líneas de
campo eléctrico, debidas a una distribución de
carga en reposo?
c) Se tienen dos cargas eléctricas puntuales opuestas situadas a una cierta distancia (dipolo eléctrico). En un plano cualquiera que contiene al segmento que une las cargas, dibuja las líneas de
campo eléctrico generado.
d) Dibuja también las líneas de intersección de las
superficies equipotenciales con el plano citado.
Oviedo 2000
Luis Ortiz de Orruño
pg 7 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
58.- Una partícula de polvo de 1,0 10 –11 g de
masa posee una carga equivalente a la de 20 electrones y se encuentra en equilibrio entre dos placas paralelas, horizontales, con una diferencia de
potencial de 153 V. Suponiendo el campo uniforme:
a) ¿Cuánto distan las placas?
b) ¿En qué sentido y con qué aceleración se moverá la partícula de polvo si se aumenta la diferencia
de potencial entre las placas en 2 V?
Datos: Carga del electrón, e 1,6 10 –19 C País
Vasco 2000 , 5,0 10 –3 m; hacia arriba(sentido
contrario al peso) 0,12 ms –2
59.- Un dipolo eléctrico está formado por dos
cargas puntuales de 2 μC y – 2 μC distantes entre
sí 6 cm. Calcula el campo y el potencial eléctrico:
a) En un punto de la mediatriz del segmento que
las une, distante 5 cm de cada carga
b) En un punto situado en la prolongación del
segmento que las une y a 2 cm de la carga positiva.
Dato: K = 9 10 9 S.I. Comunidad Valenciana 2000;
r
r
8,64 ⋅ 106 i N / C ; 0 V ; − 106 i ; 675000 V
60.- a) Explica el concepto de campo eléctrico
creado por una o varias partículas cargadas. (1 p.)
b) Dos partículas con
carga q = 0,8 μC, cada
una, están fijas en el vacío
y separadas una distancia d
= 5 m. Determina el vector
campo eléctrico que
producen estas cargas en el
punto A, que forma un
triángulo equilátero con
ambas. (1 p.)
c) Calcula el campo y el potencial eléctricos en el
punto medio entre las cargas, B. (1 p.)
Constante de Coulomb:
K= 1
= 9 ⋅10 9 N m 2 C −2 Zaragoza Junio
(4πε 0 )
r N
2001; 498,8 j
; 0; 5760 V
C
61.- ¿Qué son las líneas de campo y las superficies equipotenciales? ¿Pueden cortarse entre sí
b) Discute razonadamente la afirmación siguiente:
"Una carga o una masa en movimiento en presencia de un campo eléctrico o gravitatorio, respectivamente, se mueven siempre siguiendo la trayectoria de las líneas del campo” Cantabria 2001
62.- En una región del espacio existe un campo
eléctrico uniforme dirigido a lo largo del eje X. Si
trasladamos una carga q = +0,5 C desde un punto
del eje cuyo potencial es de 10 V a otro punto situado 10 cm a su derecha, el trabajo realizado por
la fuerza eléctrica es W =–100 J.
a) ¿Cuánto vale el potencial eléctrico en el segundo punto?
D:\2ºbachiller\caelectrico\caele09.doc
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
b) ¿Cuánto vale el campo eléctrico en dicha región?
c)¿Qué significado físico tiene que el trabajo que
realiza la fuerza eléctrica sea negativo? . Cantabria 2001
63.- Dos esferas conductoras aisladas y suficientemente alejadas entre sí, de 6 y 10 cm de radio,
están cargadas cada una con una carga de 5 10 –8
C. Las esferas se ponen en contacto mediante un
hilo conductor y se alcanza una situación de equilibrio. Calcula el potencial al que se encuentra cada una de las esferas, antes y después de ponerlas
en contacto, y la carga de cada esfera cuando se
establece el equilibrio. Dato: K = 9 10 9 N.m 2 C –2
Castilla La Mancha 2001;7500V; 4500V; 5625V;
3,75 10 –8 C; 6,25 10 –8 C
64.- Dos cargas puntuales de 2 y –2 μC cada una
están situadas respectivamente en (2,0) y en (–2,0)
( en metros). Calcula:
a) El campo eléctrico en (0,0) y en (0,10).
B) El trabajo necesario para transportar una carga
q’ de – 1 μC desde (1,0) a (–1,0)
Dato k = 9 10 9 N m 2 /C 2 Galicia 2001.
65.- Tres cargas positivas, de 5 nC cada una de
ellas, se encuentran en los vértices de un triángulo
equilátero de 12 cm de lado.
a) Halla el campo eléctrico en el punto medio de
uno de los lados de triángulo.
b) Halla el potencial eléctrico en el punto medio
de uno de los lados d triángulo.
c) Halla el punto en que el campo eléctrico es cero. Dato: K =9,0 10 9 n m 2 /C 2 Baleares 2001
66.- Un electrón, inicialmente en reposo, se pone en movimiento mediante la aplicación de un
campo eléctrico uniforme. ¿Se desplazará hacia
las regiones de mayor potencial electrostático o
hacia las de menor? ¿Qué ocurrirá si consideramos
un protón? Canarias 2001
67.- Se tienen tres cargas puntuales localizadas
como se indica en el dibujo
Calcula:
a) La intensidad del campo eléctrico en el punto
P1
b) El potencial eléctrico en el punto P 2
c ) El trabajo necesario para trasladar una cuarta
carga desde el infinito hasta el punto P 2
Datos: q 1 =q 2 =q 3 =+1 μC q 4 = –2 μC; K = 9 10 9 N
Luis Ortiz de Orruño
pg 8 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
r
m 2 C –2 Canarias 2001; 2152 j N / C ;7296 V;
+0,014 J
68.- Se disponen cuatro cargas en los vértices de
un cuadrado centrado en el
origen como se
indica a continuación: q en (-a, a), 2 q en (a, a), 3 q en (a, -a), y 6 q en (-a, -a). Calcula:
a) El campo eléctrico en el origen.
b) El potencial en el origen.
c) Se sitúa una quinta carga +q en el origen y se
libera desde el reposo. Calcula su velocidad cuando se encuentre a una gran distancia desde el origen. La Rioja 2001
69.- Tenemos una carga de –4 e en el origen,
r
una de 2 e en el punto –4 i nm y otra de 2 e en el
r
punto 4 i nm .Calcula:
r
a) El potencial eléctrico en el punto 3 j
b) El campo eléctrico en dicho punto.
c) La energía potencial eléctrica del conjunto de
las cargas.
1
Datos:
= 9 ⋅10 9 en unidades del SI. e =1,6
4πε 0
r
10 –19 C Murcia 2001; –0,768 V; − 5,0 108 j N / C ; –
8,05 10 –19 J
70.- Sean dos cargas puntuales a las que se mantiene en reposo y separadas una distancia dada. Si
el potencial en los puntos del espacio que equidistan de las dos cargas es nulo:
a) ¿Qué se puede afirmar acerca de las cargas?
(Razónalo utilizando el concepto de potencial y el
principio de superposición).
b) Dibuja las líneas del campo eléctrico y las superficies equipotenciales Oviedo 2001
71.- Sean dos cargas puntuales Q 1 = –q y Q 2 =
+4 q colocadas a una distancia d. Razona y obtén
en que punto de la línea indefinida por las dos
cargas, el campo es nulo. Oviedo 2001
72.- Explica el concepto de potencial eléctrico.¿Qué potencial eléctrico crea una carga puntual? Dibuja sus superficies equipotenciales(1p)
b) Dos partículas con igual carga, q = 3 μC , están
separadas una distancia L= 3 m. Calcula el potencial y el campo eléctricos en el punto medio entre
ambas(1,5 p)
Constante de Coulomb
1
K=
= 9 ⋅ 109 N m 2C − 2 Zaragoza Junio 2002;
4πε
36000 V; 0 N/C
73.- a) Escribe y comenta la Ley de Coulomb. (1
p.)
b) Cuatro partículas de igual carga, q = 2 μC, están situadas en los vértices de un cuadrado de lado
L=20 cm. Indica mediante una figura la dirección
y sentido de la fuerza eléctrica total que actúa so-
D:\2ºbachiller\caelectrico\caele09.doc
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
bre cada una de ellas.
Calcula el módulo de estas fuerzas. (1,5 p.)
Constante de Coulomb: K =
1
= 9 ⋅ 10 9 Nm 2 C − 2 Zaragoza Septiembre 2002;
4πε 0
1,72 N
74.- Dos cargas puntuales iguales, de –1,2 10 –6
C cada una, están situadas los puntos A (0,8) m y
B (6,0) m. Una tercera carga, de –1,5 10 –6 , se sitúa en el punto P (3,4) m.
a) Representa en un esquema las fuerzas que se
ejercen entre las cargas y calcula la resultante sobre la tercera carga.
b) Calcula la energía potencial de dicha carga.
r
Dato: K=910 9 N . m2. C –2 Andalucía 2002; R = 0 ;
6,48 10 –3 J
75.- Dos cargas puntuales positivas e iguales
( + Q ) se encuentran sobre el eje X. Una de ellas
está en x = -a y la otra en x = +a. Calcula la inten-
r
sidad del campo eléctrico, E .y el potencial electrostático, V, en el origen de coordenadas.
Si, además de las anteriores, se coloca una tercera
carga de valor –2Q en x = –2a, ¿cuáles serán los
r
r
nuevos valores de E y V? Asturias 2002; E = 0 ;
r
Q
Q
Q
18 ⋅ 10 9 V ; 4,5 ⋅ 10 9 2 − i N / C 9 ⋅ 10 9 V
a
a
a
( )
76.- Dos cargas puntuales positivas e iguales, de
valor q = 3 μC y de masa m = 5 10–3 kg se fijan
en los puntos A y B respectivamente, a una distancia d = 6 cm. Desde el punto O, situado a una
altura h = 4 cm, se lanza verticalmente hacia el
punto medio del segmento AB una tercera carga Q
= 1 μC, de masa igual a las anteriores, m.
Si al llegar al punto
M la velocidad de la partícula es cero, ¿con qué
velocidad inicial vo fue lanzada desde O?
b) Si cuando llega la tercera partícula a M con velocidad cero, se liberan simultáneamente las cargas situadas en A y B y la superficies es comple-
Luis Ortiz de Orruño
pg 9 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
tamente lisa, describe el movimiento de las tres
cargas. ¿Cuál sería la velocidad final de cada una
de ellas pasado un tiempo muy largo?
1
Datos:
= 9 ⋅ 10 9 Nm 2 C − 2 ; g= 9,8 m/s 2 Canta4πε 0
bria 2002; 16,97 m/s
77.- Una pequeña esfera de 0,2 g de masa pende
de un hilo entre dos láminas paralelas verticales
separadas 8 cm. La esfera tiene una carga de 510 –9
C y el hilo forma un ángulo de 30° con la vertical.
a) Realiza un diagrama con las fuerzas que actúan
sobre la esfera.
b) ¿Qué campo eléctrico actúa sobre la esfera?
¿Cuál es la diferencia de potencial entre las láminas? Castilla-La Mancha 2002; 2,28 10 5 N/C ;
18080 V
78.- Una bola de 0,2 g de masa y con una carga
de 5 10 -6 C está suspendida por un hilo en el interior de un campo eléctrico de intensidad
r
r
E = −200k N / C . Determina la tensión del hilo en
los siguientes casos
a) Si la carga es positiva.
b) Si la carga es negativa.
c) Si pierde la carga. Castilla-La Mancha 2002;
2,96 10–3 C; 9,6 10–4 N; 1,96 10–3 N
79.- ¿Pueden cortarse dos líneas de fuerza en un
campo eléctrico? ¿Y dos superficies equipotenciales? Razona la respuesta. Castilla v León. 2002
80.- Dadas dos cargas eléctricas, q 1 = 100 μC situada en A (-3,0) y q 2 = 50 μC situada en B (3,0)
(las coordenadas están expresadas en metros), calcula:
a) El campo eléctrico y el potencial en el punto O
(0, 0).
b) El trabajo que hay que realizar para trasladar
una carga de –2C desde el infinito hasta O.
Datos: K= 9 10 9 Nm2 C –2 Galicia 2002
81.- Una carga eléctrica se mueve en una región
en la cual tan solo hay un campo eléctrico variable:
a) Si pasa, con una determinada velocidad, por un
punto, P, en el cual el campo eléctrico es nulo, ¿se
detendrá?
b) Si se deja la carga, inicialmente en reposo, en
un punto, Q, en el cual el potencial eléctrico es
nulo, ¿continuará la carga en reposo?
Razona las respuestas I s las Ba leares. 2002
82.- En el átomo de hidrógeno, el electrón se
encuentra sometido al campo eléctrico y gravitatorio creado por el protón.
a) Dibuja las líneas del campo eléctrico creado
por el protón así como las superficies equipotenciales.
b) Calcula la fuerza electrostática con que se
atraen ambas partículas y compárala con la fuerza
gravitatoria entre ellas, suponiendo que ambas
partículas están separadas una distancia de 5,2 10 -
D:\2ºbachiller\caelectrico\caele09.doc
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
11
m.
c) Calcula el trabajo realizado por el campo eléctrico para llevar al electrón desde un punto P1 , situado a 5,2 10 -11 m del núcleo, a otro punto P2 , situado a 8 10 –11 m del núcleo. Comenta el signo del
trabajo.
Datos: K=9 10 9 N . m2 C –2 ; G=6,7 10 -11 N . m2 kg –2 ;
me = 9,1 10 –31 kg ; mp = 1,7 10 –27 kg; q e = –1,6 10 –
19
C ; q p = 1,6 10 –19 C. Islas Canarias.2002; 3,82
10–47 N despreciable en comparación con la FelécF
trica elec = 2,23 ⋅ 10 39 ; –1,55 10–18 J
Fgrav
83.- Una bola de caucho de 2 g de masa está
suspendida de una cuerda de 20 cm de longitud y
de masa despreciable en un campo eléctrico cuyo
r
r
valor es E = 10 i N / C . Si la bola está en equilibrio cuando la cuerda forma un ángulo de 15º
con la vertical, ¿cuál es la carga neta de la bola?
La Rioja 2002; 5,25 10 –6 C
3
84.- Se tienen tres cargas situadas en los vértices de un triángulo equilátero cuyas coordenadas
(expresadas en cm) son:
(
) (
)
A(0,2), B − 3 ,−1 , C 3 ,−1 . Sabiendo que las cargas situadas en los puntos B y C son idénticas e
iguales a 2 μC y que el campo eléctrico en el origen de coordenadas (centro del triángulo) es nulo,
determina:
a) El valor y el signo de la carga situada en el
punto A.
b) El potencial en el origen de coordenadas
dato: Constante de Coulomb k = 9 10 9 N m 2 C –2
Madrid.2002; +2μC; 27000 V
85.- a) Explica el concepto de campo eléctrico.
¿Qué campo eléctrico crea una partícula con carga
q? (1 p.)
b) Dos partículas con cargas q 1 = 1 μC y q 2 = 2 μC
están separadas una distancia d= 0,6 m. determina
el campo eléctrico(módulo, dirección y sentido)
en el punto medio entre las dos cargas, P. ¿Cuál es
el potencial eléctrico en este punto? (1,5p)
1
k=
= 9 ⋅ 109 Nm 2C − 2 Zaragoza Junio 2003;
4πε 0
r
− 10 5 i N / C , 9 10 4 V
86.- a) Explica el concepto de energía potencial
eléctrica. ¿Qué energía potencial eléctrica tiene
Luis Ortiz de Orruño
pg 10 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
una partícula con carga q situada a una distancia r
de otra partícula con carga q'? (1,5 p.)
b) Una partícula de masa m = 1 mg y con carga q
= 0,1 μC es acelerada mediante un campo eléctrico entre dos electrodos, partiendo del reposo, hasta que alcanza una velocidad v o = 30 m/s. Calcula
la diferencia de potencial entre los electrodos.
Con la velocidad v o indicada, la partícula se dirige
en línea recta hacia otra partícula con la misma
carga q, fija en el espacio e inicialmente muy alejada. Calcula la distancia de máxima aproximación entre ambas partículas. (1,5 p.)
1
K=
= 9 ⋅ 10 9 N m 2 C -2 . Zaragoza Septiembre
4πε 0
2003; 4500 V; 0,2 m
87.- Se tienen tres cargas situadas cada una de
ellas en tres de los vértices de un cuadrado de 8 m
de lado, tal como indica la figura. Calcula:
a) La fuerza resultante (en modulo, dirección y
sentido) que se ejerce sobre la carga situada en el
vértice A.
b) El trabajo necesario para trasladar la carga situada en el vértice A hasta el punto B. Interpreta
el signo del resultado obtenido
Nota: Resulta imprescindible incluir los diagramas y esquemas oportunos. Castilla y León 2003
r
r
; − 1,5 ⋅ 10 −4 i − 4,1 ⋅ 10 −4 j N ;VA =-2113,5 V; VB =
189V; –2,3 10–3 J, Las cargas positivas van solas de
mayores a menores potenciales, al revés habrá que
realizar un trabajo sobre ella.
88.- En el rectángulo mostrado en la figura los
lados tienen una longitud de 5 cm y 15 cm, y las
cargas son q 1 =–μC y q 2 = + 2,0 μC
a) Calcula el módulo, la dirección y el sentido del
campo eléctrico en los vértices A y B.
D:\2ºbachiller\caelectrico\caele09.doc
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
b) Calcula el potencial eléctrico en los vértices A
y B.
c) Determina el trabajo que realiza la fuerza del
campo eléctrico para trasladar a una tercera carga
de +3μC desde el punto A hasta el punto B. Dato:
K = 9 l0 9 Nm 2 /C 2 Comunidad Valenciana 2003
89.- Dos cargas puntuales q 1 = –2 μC y q 2 = +
1 μC están fijas y separadas una distancia de 60
cm. Calcula:
El campo eléctrico en el punto A, que se encuentra en el punto medio entre las cargas.
b) El potencial eléctrico en los puntos A y B.
c) El trabajo realizado por el campo cuando una
carga, q’ de +3 μC , se desplaza desde el punto B
hasta el punto A.
Datos: AB = 40cm; K=9 109 Nm 2 /C 2 ; l μC = 10 –6 C
r
Castilla-La Mancha 2003 ; –3 105 i N/C; VA= –
30000 V ; VB= –18000 V; 3,6 10–2 J ; como la carga
es positiva se moverá sola de mayor a menor potencial, realizando un trabajo
90.- Dos pequeñas bolitas, de 20g cada una, están sujetas por hilos de 2,0 m de longitud suspendidas de un punto común. Cuando ambas se cargan con la misma carga eléctrica, los hilos se separan hasta formar un ángulo de 15º. Suponiendo
que se encuentran en el vacío, próximas a la superficie de la Tierra:
a) Calcula la carga eléctrica comunicada a cada
bolita.
b) Se duplica la carga eléctrica de la bolita de la derecha. Dibuja en un esquema las dos situaciones (antes
y después de duplicar la carga de una de las bolitas)
e indica todas las fuerzas que actúan sobre ambas
bolitas en la nueva situación de equilibrio.
Datos: K = 9 10 9 N m 2 C –2 ; g= 10 m s –2 Andalucía 2003; 8,9 10 –7 C
91.- Tres cargas iguales, de 1 C cada una, se colocan en tres de los vértices de un cuadrado de lado 10 cm. Calcula.
a) El campo y el potencial eléctricos existentes en
el centro del cuadrado
b) ¿Qué carga hay que poner en el cuarto vértice
del cuadrado para que el campo sea nulo en el
centro? ¿Es nulo el potencial total en ese caso?
Luis Ortiz de Orruño
pg 11 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
c) La fuerza que actúa sobre una cualquiera de las
tres cargas en la situación inicial. (Elige una de
las tres).
1
Dato:
= 9 ⋅ 10 9 Nm 2 C –2 Cantabria 2003
4πε 0
que se anula el potencial eléctrico.
c) La fuerza eléctrica que experimenta la carga en
el origen debido ala otra.
1
= 9 ⋅ 10 9 en unidades del 5.1. Murcia 2003
4πε 0
92.- Una carga puntual q = 1/3 10 -8 C esta situada en el origen de coordenadas. Dibuja las superficies equipotenciales a intervalos de 25 V desde
50 V hasta 100 V ¿están igualmente espaciadas?
Dato: K = 9 10 9 N m 2 /C 2 Castilla-La Mancha
2003; no están igualmente espaciadas, 0,3 0,4 y
0,6 m
97.- Un objeto que tiene una carga neta de 24
μC se coloca en un campo eléctrico uniforme de
610 N/C dirigido verticalmente. ¿Cuál es la masa
de este objeto si «flota» en el campo? La Rioja 2003
93.- Un cuerpo tiene una masa de 0,1 kg y está
cargado con l0 –6 C ¿A qué distancia por encima de
él se debe colocar otro cuerpo cargado con –10 –5 C
para que el primero esté en equilibrio? Toma g =
10 m/s Extremadura 2003; 0,3 m
94.- Una partícula de 5 g de masa y una carga de
–2μC se deja en libertad en reposo a 0,5 m de dos
cargas fijas de 5 μC cada una y separadas 0,6 m. Suponiendo que solo intervienen las fuerzas eléctricas. Determina:
a) El campo eléctrico en el punto en que hemos
dejado la partícula.
b) El potencial en este punto.
c) La velocidad que tendrá la partícula cuando llegue
al punto medio entre las dos cargas Islas Baleares
r
2003; 288 000 j N / C ; 180000 V; 9,8 m/s
95.- Un protón se encuentra situado en el origen
de coordenadas del plano XY Un electrón, inicialmente en reposo, está situado en el punto (2, 0). Por
efecto del campo eléctrico creado por el protón (supuesto inmóvil). el electrón se acelera. Estando todas las
coordenadas expresadas en μm, calcula:
a) El campo eléctrico y el potencial creado por el
protón en el punto (2, 0).
b) La energía cinética del electrón cuando se encuentra en el punto ( 1 , 0 ).
c) La velocidad y el momento lineal del electrón en
la posición (1, 0).
d) La longitud de onda de De Broglie asociada al
electrón en el punto (1, 0).
Datos: Constante de la ley de Coulomb: K = 9 109 N
m2 C-2
Valor absoluto de la carga del electrón: e = 1,6 1019
C
Masa del electrón: me = 9,1 10 -3I kg
Constante de Planck: h = 6,63 10-34 J s Madrid
r
2003 ; 360 i N/C; 7,2 10 –4 V ; 1,15 10 –22 J ; 15898
r
m/s; –1,44 10 –26 i Kgm/s; 4,58 10 –8 m
96.- Tenemos una carga de – 4 10 -6 C en el ori-
r
gen y otra de 2 10 -6 C en el punto 6 i i cm. Determina:
a) El campo eléctrico en el punto medio entre ambas cargas.
b) El punto del segmento que une dichas cargas en
D:\2ºbachiller\caelectrico\caele09.doc
98.- a) Escribe y comenta la Ley
de Coulomb. (1 p.)
b) Las cuatro partículas de la figura están fijas en los vértices de un
cuadrado de lado L = 30 cm. Sus
cargas son q 1 = q 3 = 1 μC y q 2 = q 4
= –1 μC. Determina la fuerza eléctrica total (módulo, dirección y sentido) que actúa
1
sobre q 1 . (1,5 p.) k =
= 9 ⋅ 10 9 Zaragoza Ju4πε 0
r
r
nio 2004; 0,06i − 0.06 j N / C
99.- En un punto P exterior a una esfera fija y
uniformemente cargada, el potencial eléctrico
(con referencia en ∞) es V = 900 V y el campo
eléctrico tiene una intensidad E = 90 N/C .
a) Determina la carga Q de la esfera y la distancia
d entre su centro y el punto P. (1,5 p.)
b) Se abandona una partícula de carga q = -1 µC
en el punto P. Calcula su energía cinética cuando choc a con la superfi-
cie de la esfera, de radio R = 10 cm.
(1 p.)
K=
1
4πε 0
= 9 . 10 9 N m 2 C -2 Zaragoza
Septiembre 2004
100.- Una partícula de masa
despreciable y carga Q = +2 . 10 –8 C se
sujeta del extremo de un muelle que a su vez se
cuelga del techo. A continuación se crea un campo
eléctrico uniforme, de intensidad E = 2,5 10 8 V/m
cuyas líneas de campo son verticales, bajo la acción del cual se observa que el muelle se alarga en
1 cm. Calcula la constante elástica del muelle Asturias 2004
101.- Considera las cargas puntuales q 1 = +100 μC,
q 2 = –50 μC y q 3 = –100. μC, situadas en los puntos
A(-3,0), B (3, 0) y C (0, 2 ), respectivamente.
Calcula, sabiendo que las coordenadas están expresadas en metros, lo siguiente:
a) El vector intensidad de campo eléctrico en el punto
(0, 0).
b) El potencial eléctrico en el punto (0. 0) .
c) El trabajo realizado por el campo para llevar una
carga de +1 μC desde el infinito hasta el punto (0,
Luis Ortiz de Orruño
pg 12 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
0).
Datos: K=9 109N m2 C–2 1μC=10–6 C Canarias 2004
102.- Dos placas paralelas horizontales están
igualmente cargadas con distinta polaridad; la diferencia de potencial entre las placas es 6000 V y
la distancia entre ellas es 3 cm.
a) Determina la intensidad del campo eléctrico
que hay entre las placas.
b) Introducimos una bolita cargada con una carga
de +2,5 10 –7 C que cuelga verticalmente de un
hilo. Determina la masa de la bolita si la tensión
del hilo es igual a cero.
c) Si invertimos ahora la polaridad de las placas,
¿cuál será el valor de la tensión del hilo?.
Las siguientes figuras representan la situación
descrita en cada apartado: g= 9,81 m/s 2 . CastillaLa Mancha 2004
103.- Dos cargas puntuales negativas e iguales,
de –10 –3 μC , se encuentran sobre el eje de abcisas, separadas una distancia de 20 cm. A una distancia de 50 cm sobre la vertical que pasa por el
punto medio de la línea que las une, se coloca una
tercera partícula(puntual) de +10 –3 μC de carga y
1 g de masa, inicialmente en reposo. Calcula:
a) El campo y el potencial eléctrico creado por las
dos primeras cargas en la posición inicial de la
tercera.
b) la velocidad de la tercera carga al llegar al punto medio de la línea de unión de las primeras.
Datos: K=9 109N m2 C–2 1μC=10–6 Solo se considera la interacción electrostática. Galicia 2004;
r
− 67,89 j ;–35,30 V; 0,017 m/s
104.- a) Explica el concepto de energía potencial
eléctrica. ¿Qué energía potencial eléctrica tiene
una partícula con carga q situada a una distancia r
de otra partícula con carga q'? (1,5 p.)
b) Tres partículas con cargas q 1 = q 2 = 3 μC y q 3 =
–3 μC están situadas, respectivamente, en los puntos de coordenadas (a, 0), (-a, 0) y (0, a), con a =
0,1 m. Calcula las energías potenciales eléctricas
de cada una de las tres partículas. (1 p.)
9
2 −2
K= 1
(4πε 0 ) = 9 ⋅10 Nm C Zaragoza Junio 2005
–1,157; –0,17; –0,17 J
105.- a) Explica qué son las líneas de fuerza de
un campo eléctrico. ¿Cómo están relacionadas con
las superficies equipotenciales? (1 p.)
b) Explica cómo son y dibuja las líneas de fuerza
y las superficies equipotenciales del campo creado
por una esfera cargada positivamente y por una
placa plana indefinida cargada negativamente. Supón que, en ambos casos, las densidades de carga
son uniformes. (1 p.) Zaragoza Septiembre 2005
D:\2ºbachiller\caelectrico\caele09.doc
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
106.- En el punto A (0, –1) se encuentra situada
una carga eléctrica q 1 = –10 μC, y en el punto B
(0, 1), otra carga eléctrica q 2 = –10 μC. Sabiendo
que las coordenadas se expresan en metros, calcula:
a) El vector intensidad de campo eléctrico en el
punto C (1, 0). Además, representa las líneas de
campo eléctrico asociado a estas dos cargas.
b) El potencial eléctrico en el punto O (0, 0).
c) El trabajo realizado por el campo eléctrico para
trasladar una carga de 10 μC desde el punto O
hasta el punto C.
Datos: K = 9 10 9 N m2 C –2 , 1 μC=10 –6 C Canav
r
rias 2005; ET = −45000 2 ⋅ i ; –18000 V; –0,53 J
la carga no se desplaza espontáneamente.
107.- Se quiere medir g a partir del periodo de
oscilación de un péndulo formado por una esfera
de cierta masa suspendida de un hilo. La esfera
tiene una carga q positiva y el péndulo se encuentra en una región con un campo eléctrico dirigido
hacia abajo: sin embargo, el experimentador no
conoce estos hechos y no los tiene en cuenta. Responde justificando tu respuesta, si el valor de la
gravedad que obtiene es mayor o menor que el real. Murcia 2006
108.- Una partícula con carga q 1 =10 –6 C se fija
en el origen de coordenadas
a) ¿Qué trabajo será necesario realizar para colocar una segunda partícula, con carga q 2 = 10 –8 C,
que está inicialmente en el infinito, en punto, P,
situado en la parte positiva del eje Y a una distancia 30 cm del origen de coordenadas?
b) La partícula de carga q 2 tiene una masa de 2
mg. Si esta partícula deja libre en el punto P, ¿qué
velocidad tendrá cuando se encuentren a 1,5 m de
distancia de q 1? (Supón despreciables los efectos
gravitatorios).
Dato Ke = 9 10 9 N m 2 C –2 Comunidad Valenciana
2005; –3 10 4 J; 15,5 m/s
109.- Dos cargas puntuales, de 3 10 –6 C, están localizadas en los puntos (0,2) y (0,–2), respectivamente. Otras dos cargas, Q, están localizadas en
(4,2) y (4,–2). Sabiendo que el campo eléctrico en
r
el origen de coordenadas es 3 10 –6 i N/C, determina el valor de Q. La Rioja 2005; 3,72 10 –15 J
110.- Un electrón y un positrón (partícula de masa igual a la del electrón y con una carga de igual
valor pero de signo positivo) se encuentran separados inicialmente una distancia de 10 –6 m; el positrón está en el origen de coordenadas y el electrón a su derecha:
Calcula:
a) El campo eléctrico en el punto medio entre ambas partículas, antes de; que empiecen a moverse
atraídas entre sí.
b) El módulo de la aceleración inicial del electrón
(o del positrón) en el momento en que empieza a
Luis Ortiz de Orruño
pg 13 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
moverse hacia la otra partícula.
c) La energía potencial eléctrica del conjunto de
las dos partículas cuando se han aproximado hasta
una distancia de 10 -7 m.
Datos: ; m e =9,1 10 –31 kg;
1
= 9 ⋅ 10 9 N ⋅ m 2 ⋅ C − 2 e = 1,6 ⋅ 10 −19 C Murcia
4πε
r
2006; 11520 i N / C ; –2,3 10 –21 J
111.- Si en un punto, A, el potencial eléctrico es
+10 V y en otro punto, B, es +6 V, razona si una
carga positiva se moverá espontáneamente de A
hacia B o de B hacia A. Castilla La Mancha 2005
W AB = −ΔE p = −q(V B − V A ) > 0
112.- Una pequeña esfera de masa m = 2 g pende
de un hilo entre dos láminas verticales cargadas
paralelas separadas 5 cm. La esfera tiene una carga de +6μC. Si el hilo forma un ángulo de 30° con
la vertical, como se indica en la figura:
a) ¿Cuál es el valor de la tensión en el hilo?
b) ¿Cuál es el valor del campo eléctrico entré las
placas?
c) ¿Cuál es la diferencia de potencial entre las
placas? ¿Cuál es la placa positiva y cuál la negativa?
Datos: g= 9,81 m/s 2 ; Castilla La Mancha 2005;
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
Datos: Carga del protón: q p = 1,60 10 –19 C. Masa
del protón: m p = 1,67 10 –27 kg. ) Navarra 2005;
1,56 10 –7 s; 2,34 10 –4 m
114.- Sean dos cargas, Q 1 y Q 2 , colocadas en los
puntos del plano XY dados por las coordenadas (d, 0) y (d, 0), respectivamente. Si Q 1t >0 y Q 2 < 0,
y se cumple que Q1 = 4 ⋅ Q2 averigua en qué pun-
tos del plano XY el campo eléctrico es nulo. Asturias 2005
115.- Dos pequeñas esferas de igual masa m y
cargas eléctricas +q y -q, respectivamente, cuelgan de sendos hilos de igual longitud. Debido a la
atracción electrostática, los hilos forman un ángulo a = 30° con la vertical, y la distancia de equilibrio entre ambas esferas vale d = 1 m.
a) Dibuja las fuerzas que actúan sobre cada esfera.
b) Calcula el valor de q.
c) Calcula los valores de las fuerzas.
Datos: m= 1 g; g = 10 m/s 2 ;
1
K=
= 9 ⋅ 10 9 N m 2 C − 2 País Vasco 2005
4π ε 0
8 10 –7 C; 0,015N 5,76 10 –3 ; 10 –2 N
116.- a) Explica el concepto de potencial eléctrico. ¿Qué potencial eléctrico crea en su entorno
una partícula con carga q? Dibuja sus superficies
equipotenciales. (1,5 p)
b) Las tres partículas de la figura, con cargas ql =
q2 = 1 μC y q3 = –1 μC, están fijas en tres vértices
de un cuadrado de lado L = 0,9 m. Determina el
potencial eléctrico en el punto P, vértice vacante
del cuadrado. (1 p.) Zaragoza Junio 2006; 7071 V
2,26 10 –2 N;1886 N/C; 94,3 Vla de la izda es positiva
113.- Considera una región del espacio en la que
r
r
hay un campo eléctrico uniforme, E = −200 j V / m
Un protón penetra en esa región con una velocir
r
r
dad: v = 3000i + 3000 j m / s
a) Dibuja la trayectoria que seguirá el protón.
b) Calcula el tiempo que transcurre desde que penetra en esa región hasta que deja de subir,
c) Calcula la altura máxima alcanzada.
D:\2ºbachiller\caelectrico\caele09.doc
117.- a) Una partícula con carga q se mueve con
r
velocidad v por una región del espacio donde
Luis Ortiz de Orruño
pg 14 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
r
existe un campo magnético B . ¿Qué fuerza actúa
sobre la partícula? Explica las características de
esta fuerza. ¿En qué circunstancias es nula? (1,5
p.)
b) En la región sombreada de la figura existe un
campo magnético de intensidad B = 5 mT, perpendicular al plano de la figura y dirigido hacia
adentro. En esta región penetra un protón, p, que
viaja con velocidad v = 3 · 10 6 m/s en dirección
r
perpendicular a las líneas de B , tal y como se indica en la figura. Describe detalladamente la trayectoria del protón en la región con campo magnético. (1 p.)
Relación carga/masa del protón: qp /mp =
9,6 · 10 7 C/kg. Zaragoza septiembre 2006
118.- a) Explica el concepto de energía potencial
eléctrica. ¿Qué energía potencial eléctrica tiene
una partícula con carga q 1 situada a una distancia
r de otra partícula con carga q 2? (1,5 p.)
b) La esfera de la figura, de radio R = 5 cm, está
fija en el espacio y tiene una carga uniformemente
distribuida Q = 10 μC. Se libera con velocidad
inicial nula una partícula con carga q = − 1 μC y
masa m = 10 g a una distancia d = 3R del centro
de la esfera. Calcula la velocidad de la partícula
cuando choca con la superficie de la esfera. (1 p.)
1
K=
= 9 ⋅ 10 9 N m 2 C − 2 .
4πε 0
Zaragoza septiembre 2006; 15,49 m/s
119.- Una carga de 2 µC está en reposo en el punto (0, 0). Se aplica un campo eléctrico uniforme
de 500 N C –1 en el sentido positivo del eje OY.
a) Describe el movimiento seguido por la partícula y la transformación de energía que tiene lugar a
lo largo del mismo.
b) Calcula la diferencia de potencial entre los
puntos (0, 0) y (0, 2) m y el trabajo realizado para
desplazar la partícula entre dichos puntos. Andalucía. Junio, 2006
120.- Una carga puntual de valor Q ocupa la posición (0, 0) del plano XY en el vacío. En un punto A del eje X el potencial es V=–120 V y el camr
r
r
po eléctrico es E = −80 i siendo i el vector unitario en el sentido positivo del eje X. Si las coorde-
D:\2ºbachiller\caelectrico\caele09.doc
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
nadas están dadas en metros, calcula:
a) La posición del punto A y el valor de Q.
b) El trabajo necesario para llevar un electrón
desde el punto B (2, 2) hasta el punto A.
Datos: Valor absoluto de la carga del electrón: e
= 1,6 10 –19 C. Constante de la ley de Coulomb en
el vacío: K= 9 10 9 N m 2 C –2 Madrid 2006; 1,5 m; –
2 10 –8 C; –9,02 10 –18 J
121.- Tres pequeñas esferas conductoras, A, B y
C, todas ellas de igual radio y con cargas q A =1µC
; q B =4µC ; q C =7µC , se disponen horizontalmente.
Las bolitas A y B están fijas a una distancia de 60
cm entre sí, mientras que la C puede desplazarse
libremente a lo largo de la línea que une A y B
a) Calcula la posición de equilibrio de la bolita C.
b) Si con unas pinzas aislantes se coge la esfera C
y se le pone en contacto con la A dejándola posteriormente libre, ¿cuál será ahora la posición de
equilibrio de esta esfera C? (1,5 puntos)
Nota: Es imprescindible incluir en la resolución
los diagramas de fuerzas oportunos. Castilla y
León 2006; a 0,2 m de A; a 0,3 m
122.- Una carga de 2 µC está en reposo en el punto (0, 0). Se aplica un campo eléctrico uniforme
de 500 N C –1 en el sentido positivo del eje OY.
a) Describe el movimiento seguido por la partícula
y la transformación de energía que tiene lugar a lo
largo del mismo.
b) Calcula la diferencia de potencial entre los puntos (0, 0) y (0, 2) m y el trabajo realizado para desplazar la partícula entre dichos puntos. Andalucía.
Junio, 2006; mov unif acelerado recto en eje Y; la
energía potencial se transforma en energía cinética;
–1000 V; +2 10–3 J
123.- Sea una partícula de masa l g, cargada positivamente y que se mueve en el seno de un campo
eléctrico uniforme E = 1 10 4 N/C cuyas líneas de
campo son perpendiculares al suelo. Inicialmente
la partícula está en reposo y a una altura de 5 metros del suelo. Si se la deja libre, la partícula toca
el suelo con la velocidad de 20 m/s. Determina el
sentido de las líneas del campo eléctrico y la carga de la partícula. Dato: toma g = 10 m/s 2 Asturias
2006
124.- Dos placas paralelas separadas una distancia de 0,03 m están conectadas a los bornes de una
batería de 900 voltios. Si suponemos que el campo
eléctrico entre ambas placas es uniforme, calcula
la intensidad de campo entre ellas.
Si se abandona un electrón en reposo en la placa
negativa, ¿cuál será su velocidad al llegar a la
placa positiva? Y si se abandona un protón en la
placa positiva, ¿cuál será su velocidad al llegar a
la placa negativa? ¿Qué relación existe entre las
energías cinéticas finales de ambas partículas?
Datos: Carga del electrón = carga del protón =
1,6 10 –19 C.; Masa del electrón: 9,1 10 –31 kg.; Ma-
Luis Ortiz de Orruño
pg 15 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
sa del protón: 1,67 10 –21 kg. País Vasco 2006;
1,78 10 7 m/s; 4,15 10 5 m/s; iguales
125.- Una carga puntual de 1 C está situada en el
punto A (0, 3) de un sistema cartesiano. Otra carga puntual de –1 C está situada en B (0, -3). Las
coordenadas están expresadas en metros. Calcula:
a) El valor del potencial electrostático en un punto C (4, 0).
b) El vector intensidad de campo eléctrico en un
punto C (4, 0). Además, dibuja las líneas del campo eléctrico asociado a las dos cargas.
c) El trabajo realizado para llevar una carga puntual de 1 C desde el infinito al punto D (1, 3).
Dato: K = 9 10 9 N m 2 C –2 J Canarias 2006; 0
r
V; − 4,32 ⋅ 10 8 j ; –7,5 10 9 J
126.- Dos cargas puntuales q, = + 2,0 nC y q 2 =1,0 nC, están fijas y separadas una distancia de 8
cm. Calcula:
a) El campo eléctrico en el punto medio entre las
cargas, T.
b) El potencial eléctrico en los puntos S y T.
c) El trabajo necesario para trasladar otra carga,
q', de 3,0 nC desde el punto S hasta el punto T.
Datos: K = 9,00 10 9 N m2 /C 2 ; 1 nC = 10 -9 C.
mp =1,7 10 –27 kg ; e=1,6 10 –19 C. Zaragoza junio
F
2007; 4.05 10 –17 J; 0,206 m; elec = 1010
Fmag
128.- Dos pequeñas esferas, de masa m = 5 g y
con carga q, cada una, se suspenden del mismo
punto mediante hilos iguales, de masa despreciable y longitud L = 0,5 m, en presencia del campo
gravitatorio terrestre. ¿Cuál debe ser el valor de la
carga q para que, en equilibrio, los hilos formen
un ángulo α= 60°? (2 p)
Considera g =10 N/kg ;
k= 1
= 9 ⋅ 10 9 Nm 2 C −2
4πε 0
Castilla La Mancha 2006
127.- Una placa horizontal cargada negativamente
crea en sus proximidades un campo eléctrico uniforme orientado tal y como se indica en la figura,
con intensidad E = 10 3 V/m. Un protón, p, penetra
en esta región, con velocidad v o = 10 5 m/s perpenr
dicular a las líneas de E y a una distancia d = 0,2
m de la placa, de forma que describe una trayectoria como la indicada en la figura.
a) Durante esta trayectoria, ¿se conserva la energía mecánica de p?
Razona tu contestación. Calcula la energía cinética de p cuando choca con la placa. (1,5 p.)
Supón que la única fuerza que actúa sobre p es la
eléctrica.
b) Calcula la distancia L al punto de impacto. (1
p)
c) Comprueba que, si el movimiento se realiza en
las proximidades de la superficie terrestre, el peso
del protón es despreciable frente a la fuerza eléctrica que actúa sobre él. (0, 5 p)
D:\2ºbachiller\caelectrico\caele09.doc
Zaragoza junio 2007; 8,95 10 –7 C
129.- a) Explica el concepto de potencial eléctrico. ¿Tiene sentido este concepto si la fuerza electrostática no fuese conservativa? (1, 3 p.)
b) Dos cargas eléctricas puntuales de valor Q 1 =–
9μC y Q 2 =+16μC están fijas en el espacio ocupando dos vértices de un triángulo rectángulo
(Ver figura).
Calcula el potencial eléctrico en los puntos A y B.
¿qué trabajo realizará el campo eléctrico para llevar una carga puntual de 2μC desde el punto B al
punto A? (1,2
Luis Ortiz de Orruño
pg 16 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
encuentra a 500 m sobre el suelo:
b) ¿Cuánta energía se libera?
c) Calcula el valor del campo eléctrico. Cantabria. Junio, 2007
p.)
= 9 ⋅10 9 Nm 2 C −2 ; 1μC=10 –6 C Zarago4πε 0
za septiembre 2007; 90000 V; 252000 V; +0,324 J
k= 1
130.- Una partícula de masa m y carga –10 -6 C se
encuentra en reposo al estar sometida al campo
gravitatorio terrestre y a un campo eléctrico uniforme E = 100 N C -1 de la misma dirección:
a) Haz un esquema de las fuerzas que actúan sobre
la partícula y calcula su masa.
b) Analiza el movimiento de la partícula si el
campo eléctrico aumentara a 120 N C -1 , y determina su aceleración.
Dato: g= l0 m s –2 . Andalucía 2007
131.- La diferencia de potencial, V B - V A , entre
dos puntos, A y B, de una región en la que hay un
campo eléctrico, vale 3 kV. ¿Qué trabajo mínimo
se ha de hacer para llevar una carga de 6 mC desde A hasta B? Baleares 2007
132.- Tres cargas positivas, de 5 nC cada una, se
encuentran en los vértices de un triángulo equilátero de 12 cm de lado:
a) Calcula el campo eléctrico en el punto medio
de uno de los lados del triángulo.
b) Calcula el potencial eléctrico en el punto medio
de uno de los lados del triángulo.
Dato: K = 9,0 10 9 N m2 /C 2 . Baleares 2007
133.- Define:
a) Intensidad de campo eléctrico.
b) Superficie equipotencial. Canarias. Junio ,
2007
134.- En el átomo de hidrógeno el electrón se encuentra a una distancia aproximada de 5,2 10 -11 m
del núcleo, donde está localizado el protón. Calcula la fuerza electrostática con que se atraen ambas
partículas y compárala con la fuerza gravitatoria
entre ellas.
Datos: G = 6,67 10 -11 N m2 kg -2 ; mp = 1,67 10 -27
kg; me = 9, 1 10 -31 kg; K= 9 10 9 N m2 . C -2 ; q p =
1,6 10 -19 C; q e = –1,6 10 -19 C. Canarias 2007
135.- a) Enuncia y comenta la expresión de la
fuerza de Coulomb entre cargas eléctricas en reposo.
En un relámpago típico, la diferencia de potencial
entre la nube y la tie rra es 10 9 V, y la cantidad de
carga transferida vale 30 C. Suponemos que el
campo eléctrico entre la nube y la tierra es uniforme y perpendicular a la tierra, y que la nube se
D:\2ºbachiller\caelectrico\caele09.doc
136.- Dos esferas conductoras aisladas, de 12 y
20 cm de radio, que se encuentran en una zona del
espacio vacío y con sus centros separados 10 m,
están cargadas cada una con una carga de 25 10 -9
C. Las cargas se ponen en contacto mediante un
hilo conductor y se alcanza una situación de equilibrio.Calcula:
a) ¿Qué fuerza se ejercen entre sí ambas esferas
cuando están aisladas'
b) El potencial al que se encuentra cada una de las
esferas antes de ponerlas en contacto.
c) La carga y el potencial de cada esfera cuando,
una vez conectadas, se establece el equilibrio.
Dato: K = 9,00 10 9 N m2 . C -2 . Castilla-La Mancha. Junio 2007
137.- En un televisor convencional de tubo de rayos catódicos, un haz de electrones es acelerado
mediante un campo eléctrico. Estima la velocidad,
de los electrones si parten desde el reposo y la diferencia de potencial entre el ánodo y el cátodo es
de 1 kilovoltio.
Datos: me = 9, 11 10 -31 kg; e = 1,602 10 -19 C. Castilla-La Mancha. Junio 2007
138.- Dos cargas, q 1 = 2 10 -6 C y q 2 = -4 10 -6 C,
están fijas en los puntos P 1 (0, 2) y P 2 (11 0), respectivamente:
a) Dibuja el campo electrostático producido por
cada una de las cargas en el punto P (1, 2), y calcula el campo total en ese punto.
b) Calcula el trabajo necesario para desplazar una
carga q = -3 10 --6 C desde el punto O(0, 0) hasta el
punto P, y explica el significado del signo de dicho Castilla y León junio 2007
139.- Define la magnitud flujo del vector campo
eléctrico. Enuncia el teorema de Gauss.
Considera las dos situaciones de la figura:
el flujo que atraviesa la esfera ¿es el mismo en
ambas situaciones?
El campo eléctrico en el mismo punto P ¿es igual
en ambas situaciones? (0,5 puntos). Razona en todo caso tu respuesta.
Castilla y León junio 2007
140.- Una carga q > 0 se encuentra bajo la acción
de un campo eléctrico uniforme. Si la carga se
desplaza en la misma dirección y sentido que el
Luis Ortiz de Orruño
pg 17 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
campo eléctrico, qué ocurre con su energía potencial eléctrica? ¿Y si movemos la carga en dirección perpendicular al campo? Justifica ambas respuestas. Comunidad Valenciana. Junio, 2007
141.- Una carga de 20 C crea un campo eléctrico.
Calcula:
a) El potencial eléctrico en un punto situado a 3 m
de la carga creadora.
b) El trabajo que hay que realizar para trasladar
una carga de -2 C desde este punto hasta otro punto situado a 4 m de la carga creadora. Extremadura. Junio, 2007
142.- Tres cargas puntuales de 2 μC se sitúan,
respectivamente, en A (0, 0) B (1, 0) y C
(1/2, 3 ) Calcula:
2
a) El campo eléctrico en los puntos D (1/2, 0) y
⎛1 1 ⎞
⎟⎟
F ⎜⎜ ,
⎝2 2 3⎠
b) El trabajo para trasladar una carga q'= 1 μC de
D a F.
c) Con este trabajo, ¿aumenta o disminuye la
energía electrostática del sistema?
Datos: Las coordenadas se dan en metros; K = 9
10 9 N m2 C –2 ; 1 μC = 10 -6 C. Galicia. Junio, 2007
143.- Cuatro partículas cargadas están colocadas
en las esquinas de un cuadrado de lado a (ver figura), de forma que las partículas que ocupan esquinas opuestas tienen la misma carga:
a) Encuentra la relación entre q y q' para que la
fuerza sobre cada partícula q' sea nula.
b) Con esta relación, determina el valor de la
fuerza que actúa sobre cada carga q, en función de
q.
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
penetra en dicha región con una velocidad
r
r
v = 1 105 i m / s Calcula:
a) Su posición 1 μs después de haber penetrado en
esa región.
b) Su velocidad en ese instante de tiempo.
Datos: Carga del protón: e = 1, 60 10 -19 C; Masa
del protón: m p = 1,67 10 -11 kg Navarra 2007
146.- a) ¿Qué potencial electrostático crea una
carga puntual q' en cualquier punto de su entorno?
Explica el significado físico del potencial. (1 p.)
b) Dos partículas puntuales de cargas q 1 = 30 μC
y q 2 = –20 μC están situadas respectivamente en
los puntos de coordenadas (-a, 0) y (a, 0) con a =
r
10 cm. Determina el campo electrostático E (módulo, dirección y sentido) en el punto (0, 0). (1 p.)
c) ¿Qué trabajo tendremos que realizar para, en
presencia de las cargas citadas, trasladar una carga
puntual q = 0,2 μC desde el punto (0, 0) al punto
(a, a)? (1 p)
K= 1
= 9 ⋅ 10 9 N m 2 C −2 Zaragoza septiem4πε 0
bre 2008
147.- a) Explica el concepto de campo electrostático creado por una o más cargas eléctricas. ¿Es
conservativo dicho campo? Justifica la respuesta.
(1,5 puntos).
b) Tres partículas cargadas, q 1 = q 3 = 2 μC y q 2 =
-4 μC, están situadas, como indica la figura, en los
puntos (0,0), (4, 0) y (2,0). Determina el vector
r
campo electrostático E (módulo, dirección y sentido) en el punto A (2, 2). ¿Cuánto vale el potencial electrostático en dicho punto?
Las coordenadas están expresadas en metros. (1,5
puntos).
–6
9
2 −2
K= 1
(4πε 0 ) = 9 ⋅10 N m C ; 1 μC = 10 C
La Rioja junio 2007
144.- Dos partículas con cargas de +l μC y de -1
μC están situadas en lo puntos del plano XY de
coordenadas (-1,0) y (1,0), respectivamente. Sabiendo que las coordenadas están expresadas en
metros, calcula:
a) El campo eléctrico en el punto (0, 3).
b) El potencial eléctrico en los puntos del eje Y.
c) El campo eléctrico en el punto (3, 0).
d) El potencial eléctrico en el punto (3, 0).
Dato: Constante de la ley de Coulomb: K = 9 10 9
N m2 C -2 . Madrid. Junio, 2007
145.- En una región del espacio existe un campo
r
r
eléctrico uniforme E = − 1 103 i N / C Un protón
D:\2ºbachiller\caelectrico\caele09.doc
Zaragoza junio 2009
148.- a ) Enuncia y comenta la Ley de Coulomb. A
partir de ella determina el trabajo necesario para
traer una carga q’, en presencia de otra carga q,
desde el infinito hasta un punto genérico. (1,5
puntos)
b ) Dos partículas cargadas, q 1 = q 2 = 2 μC están situadas, como indica la figura, en los puntos (0,0)
y (4, 0). Determina el valor del potencial electros-
Luis Ortiz de Orruño
pg 18 de 33
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.htm
mailto:lortizdeo@hotmail.com
tático en el punto A (2,2). ¿Qué trabajo tendríamos que realizar para trasladar, desde el punto A
(2,2) al punto B (2,0), una carga q 3 = 4 μC? (1,5
puntos).
I.E.S. Francisco Grande Covián
26 de septiembre de 2009
Campo Eléctrico
Física 2ªBachiller
Las coordenadas están expresadas en metros.
1
K=
= 9 ⋅ 10 9 Nm2 C –2 ; 1 C = 10 –6 C
4πε
Zaragoza septiembre 2009
S Problemas resueltos, localizables en la página web
http://www.educa.aragob.es/iesfgcza/depart/depfiqui.ht
m
D:\2ºbachiller\caelectrico\caele09.doc
Luis Ortiz de Orruño
pg 19 de 33