Cuadricas
Anuncio
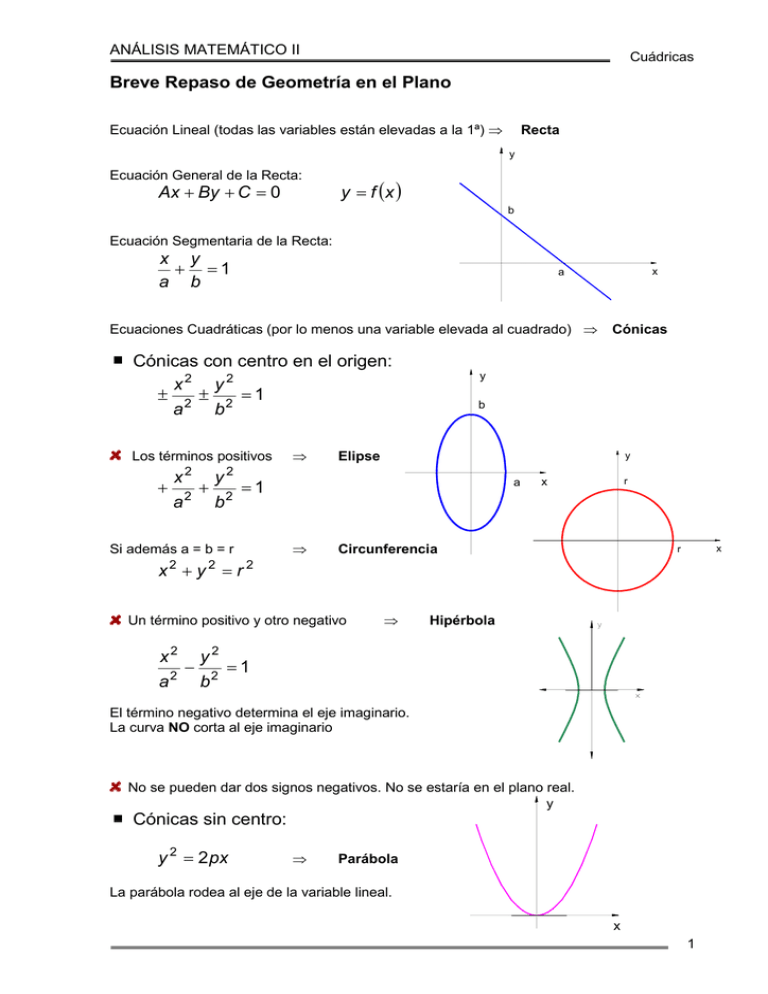
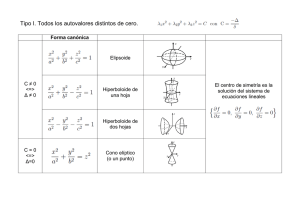
ANÁLISIS MATEMÁTICO II Cuádricas Breve Repaso de Geometría en el Plano Ecuación Lineal (todas las variables están elevadas a la 1ª) ⇒ Recta y Ecuación General de la Recta: Ax + By + C = 0 y = f (x ) b Ecuación Segmentaria de la Recta: x y + =1 a b Ecuaciones Cuadráticas (por lo menos una variable elevada al cuadrado) ⇒ Cónicas con centro en el origen: x2 y 2 ± 2 ± 2 =1 a b Los términos positivos + x 2 a2 + y 2 b2 x a ⇒ y b Elipse y =1 Si además a = b = r a ⇒ Cónicas r x Circunferencia x r x2 + y 2 = r 2 Un término positivo y otro negativo x2 a2 − y2 b2 ⇒ Hipérbola =1 El término negativo determina el eje imaginario. La curva NO corta al eje imaginario No se pueden dar dos signos negativos. No se estaría en el plano real. y Cónicas sin centro: y 2 = 2 px ⇒ Parábola La parábola rodea al eje de la variable lineal. x 1 ANÁLISIS MATEMÁTICO II Cuádricas Funciones de dos Variables Una función de dos variables en geometría representa una superficie en el espacio de tres dimensiones (R3). z = f (x, y ) ⇒ Dominio formado por dos variables independientes. z z0 y0 y z0 = posición de la imagen que corresponde al punto del dominio (x0 , y0) x0 x Ecuación Lineal (todas las variables están elevadas a la 1ª) ⇒ Plano z c Ecuación General del plano: Ax + By + Cz + D = 0 Ecuación Segmentaria del Plano: x y z + + =1 a b c b y a x Ecuaciones Cuadráticas (por lo menos una variable elevada al cuadrado) ⇒ Cuádricas Superficies Cuádricas: Cuádricas con centro en el origen: ± x2 a2 ± y2 b2 ± z2 c2 =1 Variando los signos positivos y negativos se obtienen los distintos tipos de superficies. En este tipo de superficies existe una triple simetría, por lo tanto son simétricas respecto al punto de intersección entre las superficies. Entonces podemos decir que son simétricas respecto a un centro. 2 ANÁLISIS MATEMÁTICO II Cuádricas Los tres términos cuadráticos positivos: ELIPSOIDE x2 a2 + y2 b2 + z2 c2 =1 Trazas de un elipsoide: Traza con el plano “xy”, z = 0 x2 a2 + y2 b2 =1 elipse a b c Traza con el plano “xz”, y = 0 x2 a2 + z2 c2 =1 a elipse Traza con el plano “yz”, x = 0 y2 b2 + z2 c2 =1 c elipse b Si una de las trazas es una circunferencia, se llama elipsoide de revolución. De acuerdo a los valores de los parámetros el elipsoide puede tomar distintas posiciones. 3 ANÁLISIS MATEMÁTICO II Cuádricas En el caso de que todos los parámetros sean iguales, es decir, a = b = c = r, se tiene una esfera. x 2 + y 2 + z2 = r 2 Dos términos cuadráticos positivos y uno negativo: HIPERBOLOIDE DE UNA HOJA − x2 a 2 + y2 b 2 + z2 c 2 =1 El hiperboloide NO corta al eje de la variable que está en el término negativo. 4 ANÁLISIS MATEMÁTICO II Cuádricas Trazas del hiperboloide de una hoja: Traza con el plano “xy”, z = 0 − x2 a2 + y2 b2 -b =1 b hipérbola eje real en “y”, eje imaginario en “x”. Traza con el plano “xz”, y = 0 − x2 a2 + z2 c2 =1 c -c hipérbola eje real en “z”, eje imaginario en “x”. Traza con el plano “yz”, x = 0 y2 b2 + z2 c2 c =1 elipse b La elipse más pequeña, se llama elipse de garganta. Si en vez de tener como traza una elipse se tiene una circunferencia, la superficie se llama Hiperboloide de una hoja de revolución. Esta es una superficie reglada, es decir, que se la puede obtener mediante rectas. 5 ANÁLISIS MATEMÁTICO II Cuádricas De acuerdo a los valores de los parámetros el hiperboloide de una hoja puede tomar distintas posiciones. Un término cuadrático positivo y dos negativos: HIPERBOLOIDE DE DOS HOJAS − x2 a2 − y2 z2 + b2 c2 =1 El hiperboloide NO corta al plano formado por los ejes de las variables que están en los términos negativos. Trazas del hiperboloide de dos hojas: Traza con el plano “xy”, z = 0 − x2 a2 − y2 =1 b2 No existe traza. Traza con un plano paralelo al “xy”, z = d con − Como x2 a2 − d >c x2 2 a1 + , y2 b2 d2 c2 y2 2 b1 + d2 c2 =1 x2 a2 + y2 b2 d >c = d2 c2 −1 > 1. Entonces se puede llegar a: =1 elipse 6 ANÁLISIS MATEMÁTICO II Traza con el plano “xz”, y = 0 − x 2 a2 + z 2 c2 =1 Cuádricas c -c hipérbola eje real en “z”, eje imaginario en “x”. Traza con el plano “yz”, x = 0 − y2 z2 =1 c hipérbola eje real en “z”, eje imaginario en “y”. -c b 2 + c 2 Si los dos parámetros negativos tienen el mismo valor el Hiperboloide de dos hojas se dice de revolución. (se llega a a1 = b1) 7 ANÁLISIS MATEMÁTICO II Cuádricas sin centro: x2 y 2 2⋅z = ± ± p q Cuádricas PARABOLOIDES Los dos términos cuadráticos con el mismo signo: PARABOLOIDE ELÍPTICO 2⋅z = x2 y 2 + p q El paraboloide rodea al eje de la variable lineal Trazas del paraboloide elíptico: Traza con el plano “xy”, z = 0 x2 y 2 + =0 p q Punto (0,0) vértice del paraboloide. Traza con un plano paralelo al “xy”, z = d con 2⋅d = 2 d >0 2 x y + p q Entonces se puede llegar a: x2 2 p1 + y2 2 q1 =1 elipse Traza con el plano “xz”, y = 0 2⋅z = x2 p parábola que abraza al eje “z”. 8 ANÁLISIS MATEMÁTICO II Cuádricas Traza con el plano “yz”, x = 0 2⋅z = y2 q parábola que abraza al eje “z”. Si la sección normal al eje al que rodea el paraboloide es una circunferencia, es decir p = q, el paraboloide se llama de revolución. Si el vértice está desplazado sobre el eje al que rodea el paraboloide, se tiene: x2 y 2 2⋅z = + +k p q Variando los parámetros ya mencionados y sus signos se pueden tener los siguientes paraboloides: Los dos términos cuadráticos con distinto signo: PARABOLOIDE HIPERBÓLICO x2 y 2 2⋅z = − + p q Z Y X 9 ANÁLISIS MATEMÁTICO II Cuádricas Trazas del paraboloide hiperbólico: Traza con el plano “xy”, z = 0 − x2 2 p1 + y2 2 q1 =0 x y x y − + ⋅ + + = 0 p1 q1 p1 q1 Dos rectas que pasan por el origen. Traza con el plano “xz”, y = 0 x2 2⋅z = − p parábola que abraza al eje “z”, con ramas de concavidad negativas. Traza con el plano “yz”, x = 0 2⋅z = y2 q2 parábola que abraza al eje “z”, con ramas de concavidad positivas. 10 ANÁLISIS MATEMÁTICO II Cuádricas Si marcamos la intersección del paraboloide hiperbólico con planos paralelos al “xy” tenemos: z = ±d x2 y 2 2⋅d = − + p q x2 y2 − + =1 2⋅d ⋅ p 2⋅d ⋅q Que dependiendo del signo de d son hipérbolas con eje imaginario x o y. El paraboloide hiperbólico es una superficie reglada. 11 ANÁLISIS MATEMÁTICO II Cuádricas Superficies Cilíndricas: Se llama superficie cilíndrica a una superficie generada por una recta que se desplaza paralela a si misma siguiendo una curva C llamada directriz. Z O Z P(x,y,z ) Y C R(x,y,0) X Y X Si la directriz de una superficie cilíndrica es una circunferencia, la superficie se llama circular. Análogamente, tenemos superficies cilíndricas parabólicas, elípticas e hiperbólicas. 12