ejercicios
Anuncio

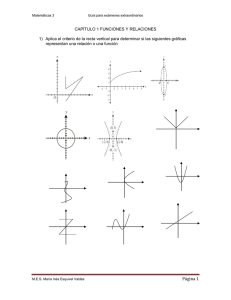
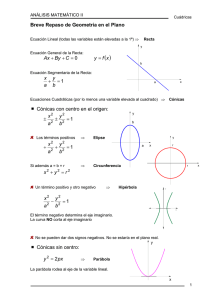
Cuádricas 1. Analizar, en cada caso, cuál es la gráfica de las superficies de ecuación Si, indicando de qué superficie se trata. S1) x2 + y2 = z S2) x2 + 4 y2 + z2 = 1 S3) – 2 x2 + y2 = z S4) x2 – y2 + z2 = 1 2. Escribir la ecuación de la traza de la superficie S) 9 x2 + 4 y2 = z en los planos π1) x = 0, π2) y = 2 y π3) z = 4 e identificar las curvas, indicando en cada caso las coordenadas de los vértices. Cuádricas 3. Encontrar la ecuación de la traza de la superficie S) 9 x2 – 4 y2 + 4 z2 = 9 en los planos π1) x = 2, π2) y = 4 y π3) z = 0 e identificar las curvas, indicando en cada caso las coordenadas de los vértices. 4. Analizar en cada caso la superficie de ecuación Si, indicando de qué superficie se trata y dando las coordenadas del centro. Graficar. S1) x2 + 2 y2 + 3 z2 – 2 x + 4 y – 12 z + 14 = 0 S2) 9 x2 + y2 + 4 z2 – 18 x + 2 y + 16 z – 10 = 0 S3) z = 4 – x2 – y2 – 2 y S4) y = x2 + z2 5. Escribir la ecuación de la superficie formada por los puntos P(x, y, z) tales que la distancia entre P y el plano π) z = – 1 sea igual a la distancia entre P y el punto R de coordenadas (0, 0, 1). Identificar la superficie. 6. Hallar la ecuación de la proyección sobre el plano x-y de la curva de intersección de los siguientes pares de superficies e identificar las curvas. el paraboloide S) x2 + y2 = z y el plano π) z = 2 x los paraboloides S1) x2 + y2 = z y S2) z = 4 – x2 – y2 el elipsoide S) x2 + 2 y2 + z2 = 2 y el plano π) z = x 7. Escribir la ecuación de la superficie formada por los puntos P(x, y, z) tales que la distancia entre P y el plano π) z = – 1 sea el doble de la distancia entre P y el punto R (0, 0, 1). Identificar la superficie. Página 2