Taller de Cálculo II 16 de octubre de 2013 UNIVERSIDAD DEL

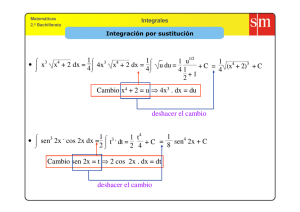
Taller de Cálculo II
16 de octubre de 2013
UNIVERSIDAD DEL CAUCA
FACULTAD DE CIENCIAS NATURALES, EXACTAS Y DE LA EDUCACION
DEPARTAMENTO DE MATEMATICAS
Taller de Cálculo II (Mat 201)
16 de octubre de 2013
Profesor: Tulio Emiro López Erazo
Oficina: Departamento de Matemáticas, Of. 307.
Email:tele2607@gmail.com
Calcule
Z
1.
Z
2.
Z
3.
Z
4.
Z
5.
Z
6.
Z
7.
Z
8.
Z
9.
Z
10.
Z
11.
Z
12.
Z
13.
Z
14.
Z
15.
Z
16.
Z
17.
cada una de las siguientes integrales indefinidas (potencias trigonométricas).
Z
sec4 (5x) dx.
18.
sen4 x dx.
√
Z
tan x
1
√
dx.
dx.
19.
x
sen4 x
Z
sen (log x)
1
dx.
20.
dx.
x
sen2 x cos4 x
Z
sen2 x dx.
21.
sec5 4x dx.
Z
sen3 6x cos 6x dx.
22.
tan2 5x dx.
sen 3x
Z
dx.
3 + cos 3x
23.
cot3 x dx.
tan x
Z
dx.
cos2 x
24.
cot4 x dx.
1 + sen 3x
Z dx.
x
x
cos2 3x
25.
dx.
tan3 + tan4
3
4
1 − sen x
dx.
Z
x + cos x
26.
x sen2 x2 dx.
sen3 x
√
dx.
Z
cos x
√
27.
sen5 x 3 cos x dx.
sen x cos x
√
dx.
Z
cos2 x − sen2 x
28.
sen 3x cos 5x dx.
p
1 + 3 cos2 x sen 2x dx.
Z
29.
sen 10x sen 15x dx.
cos3 x dx.
Z
x
x
30.
cos
cos
dx.
5
sen x dx.
2
3
Z
x
2x
31.
sen
cos
dx.
t sen2 x cos3 x dx.
3
3
Z
x
x
32.
cos(ax + b) cos(ax − b) dx.
sen3 cos5 dx.
2
2
Z
cos5 x
dx.
33.
sen ax sen(ax + b) dx.
sen3 x
Sea n ∈ N. Encontrar una fórmula de reducción para cada una de las siguientes integrales
1
Taller de Cálculo II
Z
1.
Z
2.
16 de octubre de 2013
Z
n
sen x dx.
3.
cosn x dx.
4.
Z
1
dx.
senn x
1
dx.
cosn x
Sea n ∈ N. Probar cada una de las siguientes fórmulas de reducción. Suponga n, m ∈ N.
Z
Z
n
n−1
1.
sen x dx = − sen
x cos x + (n − 1) senn−2 x cos2 x dx.
Z
Z
senn−1 x cos x n − 1
2.
senn x dx = −
+
senn−2 x dx.
n
n
Z
Z
cosn−1 x sen x n − 1
cosn−2 x dx.
3.
cosn x dx =
+
n
n
Z
Z
1 senn x
n
senn−1 x
senn+1 x
4.
dx
=
−
dx.
m+1
m
cos
x
m cos x m
cosm−1 x
Z
Z
cosm+1 x
1 cosm x m
cosm−1 x
5.
dx
=
−
dx.
n+1
n
sen
x
n sen x
n
senn−1 x
Calcule cada una de las siguientes integrales indefinidas. Use fórmulas de reducción.
Z
Z
1.
sen4 x dx.
3.
cos5 x dx.
Z
Z
1
1
2.
dx.
4.
dx.
5
sen x
cos6 x
2