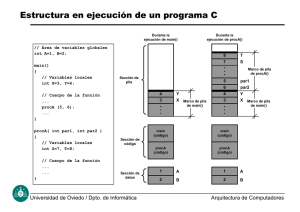
Teoría de la Demostración: Deducción Natural
Anuncio

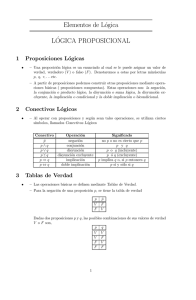
Teorı́a de la Demostración: Deducción Natural TAII(I) Axiomas, Reglas de Inferencia y Reglas derivadas para el Método de Deducción Natural (DN). 1. Deducción Natural Axiomas X-DN: 1. ` A1(α → α). Reglas de Inferencia RI-DN: Nombre Regla de Sustitución (RS) Regla Dada una tesis (axioma o teorema), el resultado de sustituir una, algunas, o todas sus variables proposicionales por fbf es también una tesis del sistema. Regla de Introducción de la Conjunción (RI ∧) Regla de Eliminación de la Conjunción (RE∧) Regla de Introducción de la Disyunción (RI∨) Regla de Eliminación de la Disyunción (RE∨) (Prueba por casos) 1 α β α∧β α∧β α α∧β β α α∨β β α∨β α ⇒ γ, β ⇒ γ α∨β ⇒γ Nombre Regla de Introducción de la Negación (RI¬) (Reducción al absurdo) Regla α ⇒ β, α ⇒ ¬β ¬α Regla de Eliminación de la Doble Negación (RE¬¬) ¬¬α α Regla de Introducción de la Implicación (RI→) (Modus Ponens) α→β α β Regla de Eliminación de la Doble Negación (RE→) (Teorema de la Deducción) α⇒β α→β Reglas derivadas de la implicación Nombre Silogismo Hipotético Regla α→β β→γ α→γ Mutación de Premisas α → (β → γ) β → (α → γ) α→γ Identidad α α 2 Nombre Introducción del Antecedente (Carga de Premisa) Regla α β→α Reglas derivadas de la conjunción1 Nombre Propiedad conmutativa Regla α∧β β∧α Propiedad asociativa (α ∧ β) ∧ γ α ∧ (β ∧ γ) Idempotencia α∧α α Recı́proca de la Idempotencia de la Conjunción α α∧α Propiedad distributiva α ∧ (β ∨ γ) (α ∧ β) ∨ (α ∧ γ) Recı́proca de la Propiedad distributiva (α ∧ β) ∨ (α ∧ γ) α ∧ (β ∨ γ) 1 La lı́nea horizontal doble significa que la inferencia puede realizarse en ambos sentidos: premisas a conclusión, o conclusión a premisas 3 Nombre Absorcion Regla α ∧ (α ∨ β) α Recı́proca de la Absorcion α α ∧ (α ∨ β) Reglas derivadas de la disyunción Nombre Propiedad conmutativa Regla α∨β β∨α Propiedad asociativa (α ∨ β) ∨ γ α ∨ (β ∨ γ) Idempotencia α∨α α Recı́proca de la Idempotencia de la Disyunción α α∨α Propiedad distributiva α ∨ (β ∧ γ) (α ∨ β) ∧ (α ∨ γ) Recı́proca de la Propiedad distributiva (α ∨ β) ∧ (α ∨ γ) α ∨ (β ∧ γ) 4 Nombre Absorcion Regla α ∨ (α ∧ β) α Recı́proca de la Absorcion α α ∨ (α ∧ β) Reglas derivadas de la negación Nombre Modus Tollens Regla α→β ¬β ¬α Contraposición α→β ¬β → ¬α Doble Negación α ¬¬α Excontradictione Quodlibet α ∧ ¬α β Tollendo Ponens α∨β ¬β α 5 Reglas de interdefinición entre conectivas Nombre Importación/Exportación Regla α → (β → γ) α∧β →γ Recı́proca de portación/Exportación la Imα∧β →γ α → (β → γ) Interdefinición Implicación/Disyunción ¬α ∨ β α→β Recı́proca de la Interdefinición Implicación/Disyunción α→β ¬α ∨ β Interdefinición Implicación/Conjunción ¬(α ∧ ¬β) α→β Recı́proca de la Interdefinición Implicación/Conjunción α→β ¬(α ∧ ¬β) Leyes de De Morgan ¬(α ∧ β) ¬α ∨ ¬β 6 Nombre Dilema Constructivo Simple Regla α∨β α→γ β→γ γ Dilema Constructivo Complejo α∨β α→γ β→η γ∨η Dilema Constructivo Simple con Negación de los Consecuentes ¬α ∨ ¬β γ→α γ→β ¬γ Dilema Constructivo Complejo con Negación de los Consecuentes ¬α ∨ ¬β γ→α η→β ¬γ ∨ ¬η Reglas derivadas de la doble implicación Nombre Introducción de la Doble Implicación Regla α→β β→α α↔β Eliminación de la Doble Implicación α↔β α→β 7 α↔β β→α