Ayudantía Nº 19 1. Una masa M se parte en dos fragmentos m y m
Anuncio
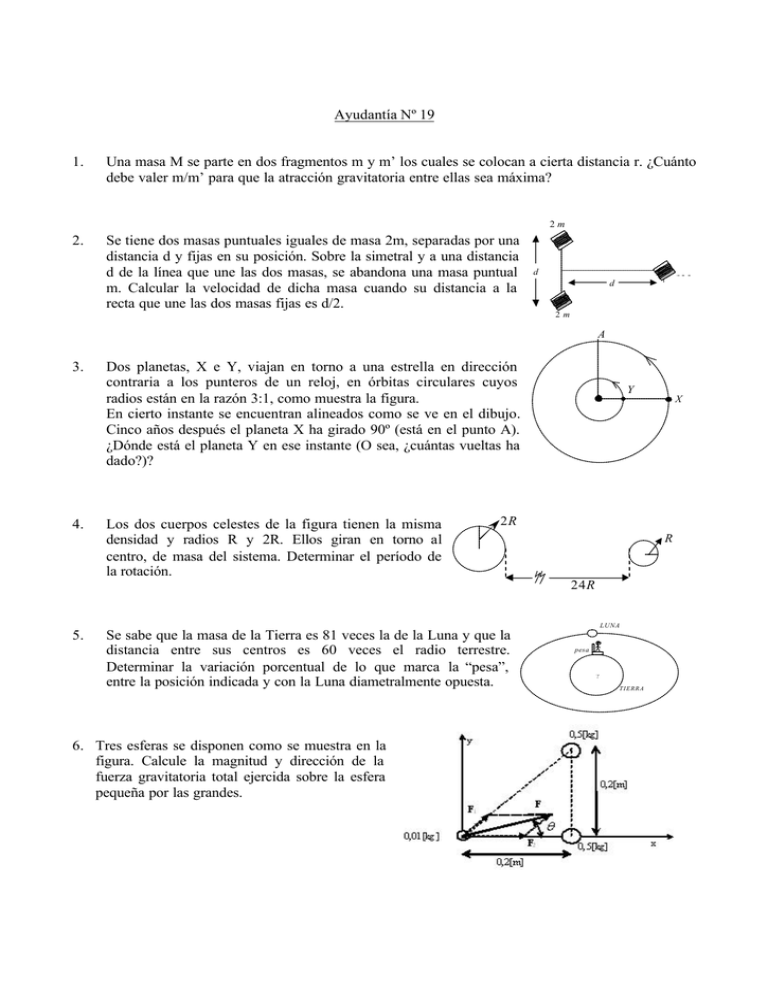
Ayudantía Nº 19 1. Una masa M se parte en dos fragmentos m y m’ los cuales se colocan a cierta distancia r. ¿Cuánto debe valer m/m’ para que la atracción gravitatoria entre ellas sea máxima? 2. Se tiene dos masas puntuales iguales de masa 2m, separadas por una distancia d y fijas en su posición. Sobre la simetral y a una distancia d de la línea que une las dos masas, se abandona una masa puntual m. Calcular la velocidad de dicha masa cuando su distancia a la recta que une las dos masas fijas es d/2. 2m d m d 2m A 3. 4. Dos planetas, X e Y, viajan en torno a una estrella en dirección contraria a los punteros de un reloj, en órbitas circulares cuyos radios están en la razón 3:1, como muestra la figura. En cierto instante se encuentran alineados como se ve en el dibujo. Cinco años después el planeta X ha girado 90º (está en el punto A). ¿Dónde está el planeta Y en ese instante (O sea, ¿cuántas vueltas ha dado?)? Los dos cuerpos celestes de la figura tienen la misma densidad y radios R y 2R. Ellos giran en torno al centro, de masa del sistema. Determinar el período de la rotación. Y 2R R 24R LUNA 5. Se sabe que la masa de la Tierra es 81 veces la de la Luna y que la distancia entre sus centros es 60 veces el radio terrestre. Determinar la variación porcentual de lo que marca la “pesa”, entre la posición indicada y con la Luna diametralmente opuesta. 6. Tres esferas se disponen como se muestra en la figura. Calcule la magnitud y dirección de la fuerza gravitatoria total ejercida sobre la esfera pequeña por las grandes. X pesa ? TIERRA 7. Se tiene un cuerpo de masa m. a) Calcular a qué altura sobre la superficie terrestre el cuerpo pesa la mitad de lo que pesa en la Tierra. b) Sabiendo que el radio de la Tierra es RT ? 6370[km] estima la masa de la Tierra. 8. La NASA quiere enviar una nave a la Luna desde la superficie terrestre, pero deben saber: a) la rapidez inicial necesaria para disparar la nave verticalmente hasta una altura sobre la Tierra igual al radio de ésta. b) la rapidez de escape, es decir, la rapidez inicial que permitiría a la nave escapar de la Tierra. Ignore la resistencia del aire y la atracción gravitatoria de la Luna. El radio de la Tierra es RE ? 6380[Km] y su masa es mE ? 5,97 ?1024 [kg] . 9. El cometa Halley se mueve en una órbita elíptica alargada alrededor del Sol. En el perihelio el cometa está a 8,75·107 [km] del Sol. En el afelio está a 5,26·109 [km]. a) ¿En qué punto tiene el cometa la máxima rapidez? b) Calcule el semieje mayor, la excentricidad y el período de la órbita. 10. Suponga que hace un agujero que atraviesa la Tierra (radio RT , masa mT ) siguiendo un diámetro y deja caer una bolsa de basura (de masa m) por él. Deduzca una expresión para la fuerza gravitatoria sobre la bolsa en función de su distancia r al centro. Suponga que la densidad de la Tierra es uniforme.








