2ωR ← ¿?
Anuncio

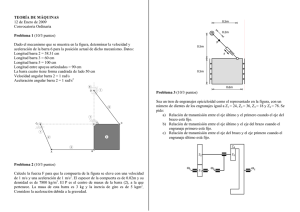
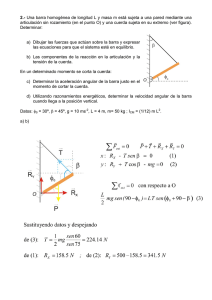
Resolución del examen de Diciembre 2009 – Problema 1 PROBLEMA 1 - RESOLUCIÓN. Para resolver la velocidad y aceleración angular de la barra A el procedimiento más directo consiste en acudir al centro del disco (C) y descomponer su velocidad y aceleración en arrastre y relativo con la barra AB: G G G vC = varrastre + vrel/barra AB G G G G aC = aarrastre + arel/barra AB + acoriolis • Movimiento de arrastre con barra AB: en el arrastre se considera que el punto C está rígidamente unido a la barra AB. Se plantean campos de velocidades y aceleraciones: JJJG JJJG JJJG G G G G G G vC = v A + ωAB ∧ AB ; aC = aA + α AB ∧ AB − ω2AB AB Tanto la velocidad como la aceleración del punto A son conocidas, por ser A punto de la barra O’A y tener ésta velocidad angular y aceleración angular conocidas (ω constante y α nula). Las incógnitas serán la velocidad angular y la aceleración angular de la barra AB. • Movimiento relativo: el movimiento relativo es cómo ve un espectador que se mueve con la barra AB el movimiento del punto C. Al estar el disco permanentemente en contacto con la barra AB, en el movimiento relativo el punto C sólo puede describir una trayectoria rectilínea paralela a la barra AB. La velocidad y aceleración relativas serán, por lo tanto, paralelas a la barra AB y de módulo desconocido. • Coriolis: la descomposición por arrastre y relativo debe incluir, en aceleraciones, el G G G G término de Coriolis: 2ωarrastre ∧ vrelativa = 2ωAB ∧ vrelativa . Siendo la velocidad relativa paralela a la barra AB, la aceleración de Coriolis será perpendicular a dicha barra; su módulo y sentido podrán determinarse una vez se hayan obtenido, del cinema de velocidades, tanto la velocidad angular de la barra AB (con su sentido) como la velocidad relativa (en módulo y sentido). Se presentan, a continuación, los cinemas de velocidad y aceleración, así como los resultados numéricos extraídos de dichas construcciones gráficas: VELOCIDADES G vC G vA JJJG G ωAB ∧ AC G v rel / AB © TECNUN, 2009 Módulo Dirección/sentido 2ωR ← ωR 3 ωAB 2R ⊥ AC (30º con vertic) ¿? // AB (60º con horiz) Resolución del examen de Diciembre 2009 – Problema 1 AB G vC ωR 3 + 2ωABR G vA AC G v rel / AB 3 3 = vrel 2 2 1 1 2ωABR + vrel = 2ωR 2 2 La resolución de estas ecuaciones conduce a: JJJG ωAB ∧ AC vrel = 3ωR (sentido indicado en la figura) ωAB = ω (saliente) 2 ACELERACIONES G aC G aA JJJG G α AB ∧ AC JJJG −ω2AB AC G arel/AB G acor © TECNUN, 2009 Módulo Dirección/sentido 2Rω2 ω2R 3 α AB 2R ⊥ AC (30º con vertic) ω2R/2 // AC (30º con horiz) hacia C ¿? 3ω2R // AB (60º con horiz) ⊥ AB (30º con horiz.) hacia abajo Resolución del examen de Diciembre 2009 – Problema 1 AC ω2R 3 + ω2R JJJG G α AB ∧ AC 2ω2R = − G aC 3 ω2R 3 2 − ω R + arel + α ABR 3 4 2 2 La resolución conduce a: AC AB 3 3 3 arel − ω2R − + α ABR = 0 4 2 2 G aA JJJG −ω2AB AC α AB = de estas ecuaciones 3 3 2 ω (entrante) 4 G acor G arel/AB AB La resolución de la velocidad angular y aceleración angular del disco de centro C pasa por el punto de rodadura (F) entre disco y barra AB. Al haber rodadura puede afirmarse que: G G vF (disco) = vF (barra) Æ JJJG G JJJG G G G vC + ωdisco ∧ CF = v A + ωAB ∧ AF G vC Siendo distancia CF = R y la distancia AF = R 3 . G vA JJJG G ωdisco ∧ CF la Resolviendo el cinema: AB JJJG G ωAB ∧ AF ωdisco = 5 ω (entrante) 2 AB En cuanto a las aceleraciones, sólo pueden igualarse las componentes de las aceleraciones en la dirección tangente al contacto (es decir en la dirección de la barra AB): JJJG JJJG G G G comp. tangente aF (disco) = aC + αdisco ∧ CF − ω2disco CF ⎯⎯⎯⎯⎯⎯⎯⎯ → (aF )t = ω2R 3 + αdiscoR JJJG JJJG G G G 3 2 3 2 comp. tangente aF (barra) = aA + α AB ∧ AF − ω2AB AF ⎯⎯⎯⎯⎯⎯⎯⎯ → (aF )t = − ωR− ωR 2 4 Igualando las componentes tangentes: αdisco = © TECNUN, 2009 7 3 2 ω (entrante) 4