operaciones y propiedades de los números enteros (conjunto z)
Anuncio
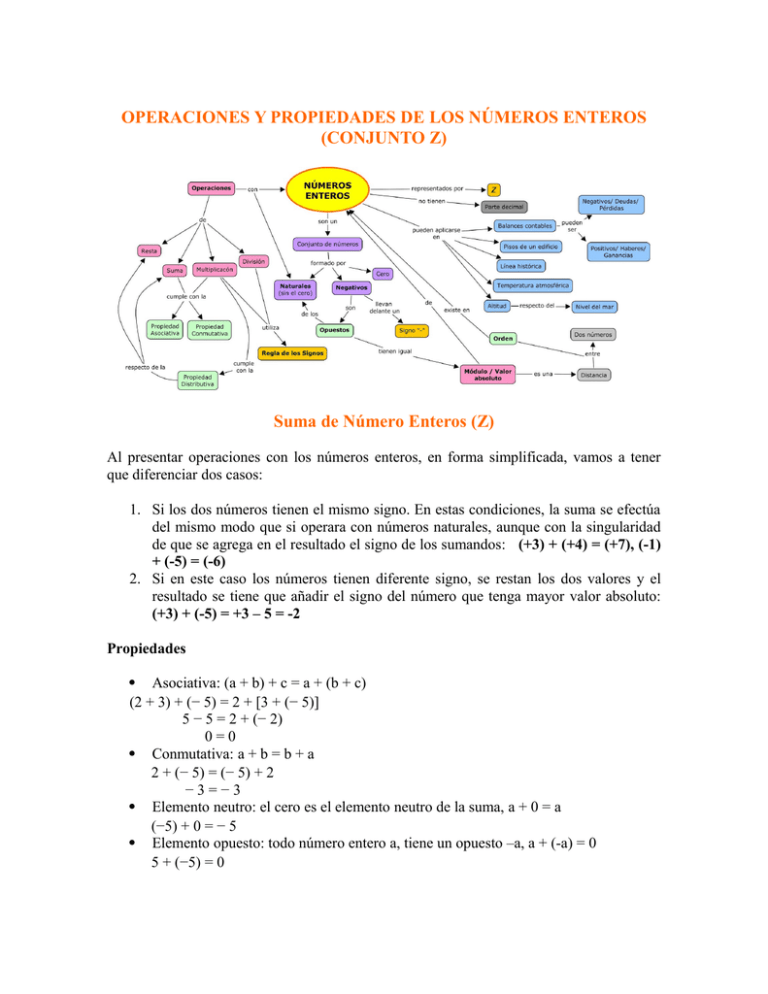
OPERACIONES Y PROPIEDADES DE LOS NÚMEROS ENTEROS
(CONJUNTO Z)
Suma de Número Enteros (Z)
Al presentar operaciones con los números enteros, en forma simplificada, vamos a tener
que diferenciar dos casos:
1. Si los dos números tienen el mismo signo. En estas condiciones, la suma se efectúa
del mismo modo que si operara con números naturales, aunque con la singularidad
de que se agrega en el resultado el signo de los sumandos: (+3) + (+4) = (+7), (-1)
+ (-5) = (-6)
2. Si en este caso los números tienen diferente signo, se restan los dos valores y el
resultado se tiene que añadir el signo del número que tenga mayor valor absoluto:
(+3) + (-5) = +3 – 5 = -2
Propiedades
Asociativa: (a + b) + c = a + (b + c)
(2 + 3) + (− 5) = 2 + [3 + (− 5)]
5 − 5 = 2 + (− 2)
0=0
Conmutativa: a + b = b + a
2 + (− 5) = (− 5) + 2
−3=−3
Elemento neutro: el cero es el elemento neutro de la suma, a + 0 = a
(−5) + 0 = − 5
Elemento opuesto: todo número entero a, tiene un opuesto –a, a + (-a) = 0
5 + (−5) = 0
Resta de Números Enteros (Z)
Multiplicación de Números Enteros (Z)
Propiedades
Interna: a · b
2 · (−5)
Asociativa: (a · b) · c = a · (b · c)
(2 · 3) · (−5) = 2· [(3 · (−5)]
6 · (−5) = 2 · (−15)
-30 = -30
Conmutativa: a · b = b · a
2 · (−5) = (−5) · 2
-10 = -10
Elemento neutro: a ·1 = a
(−5)· 1 = (−5)
Distributiva: a · (b + c) = a · b + a · c
(−2)· (3 + 5) = (−2) · 3 + (−2) · 5
(−2)· 8 = - 6 - 10
-16 = -16
Sacar factor común: a · b + a · c = a · (b + c)
(−2) · 3 + (−2) · 5 = (−2) · (3 + 5)
División de Números Enteros (Z)
La división de dos números enteros es igual al valor absoluto del cociente de los valores
absolutos entre el dividendo y el divisor, y tiene de signo, el que se obtiene de la aplicación
de la regla de los signos.
10 : 5 = 2
(−10) : (−5) = 2
10 : (−5) = − 2
(−10) : 5 = − 2
Propiedades:
No es una operación interna:
(−2) : 6
No es Conmutativo:
a:b≠b:a
6 : (−2) ≠ (−2) : 6
Potenciación en Z
1. Las potencias de exponente par son siempre positivas.
26 = 64
(−2)6 = 64
2. Las potencias de exponente impar tiene el mismo signo de la base.
23 = 8
(−2)3 = −8
Propiedades
a0 = 1
a1 = a
am · a n = am+n Ejm: (−2)5 ·(−2)2 = (−2)5+2 = (−2)7 = −128
am : a n = am - n Ejm: (−2)5 : (−2)2 = (−2)5 - 2 = (−2)3 = −8
(am)n = am · n Ejm: [(−2)3]2 = (−2)6 = 64
an · b n = (a · b) n Ejm: (−2)3 · (3)3 = (−6) 3 = −216
an : b n = (a : b) n Ejm: (−6)3 : 3 3 = (−2)3 = −8
Potencias de exponente entero negativo
Operaciones combinadas en Z
12 − {7 + 4 · 3 − [(−2)2 · 2 − 6)]}+ (22 + 6 − 5 · 3) + 3 − (5 − 23 : 2) =
Paso 1: Primero operamos con las potencias, productos y cocientes de los paréntesis.
Ejemplo:
= 12 − [7 + 4 · 3 −(4 · 2 − 6)] + (4 + 6 − 5 · 3) + 3 − (5 − 8 : 2) =
Paso 2: Operamos con los productos y cocientes de los paréntesis.
Ejemplo:
= 12 − [7 +12 − (8 − 6)] + (4 + 6 − 15) + 3 − (5 − 4) =
Paso 3: Realizamos las sumas y diferencias de los paréntesis.
Ejemplo:
= 12 − (7 + 12 − 2) + (−5) + 3 − (1) =
= 12 − (17) + (−5) + 3 − (1) =
Paso 4: La supresión de paréntesis ha de realizarse considerando que:
-Si el paréntesis va precedido del signo +, se suprimirá manteniendo su signo los términos
que contenga.
-Si el paréntesis va precedido del signo −, al suprimir el paréntesis hay que cambiar de
signo a todo los términos que contenga.
Ejemplo:
= 12 − 17 − 5 + 3 − 1 = −8
Problemas en Z
Pueden complementar este material con los siguientes links:
http://www.youtube.com/watch?v=ZgWjZUI5CH0
http://www.youtube.com/watch?v=9ie9wdb6nXY
www.amolasmates.es/.../05_Ecuaciones%20e%20inecuaciones.pdf
http://www.vadenumeros.es/tercero/ejercicios-con-parentesis.htm







