SEMANA 2 TRIGONOMETRIA
Anuncio
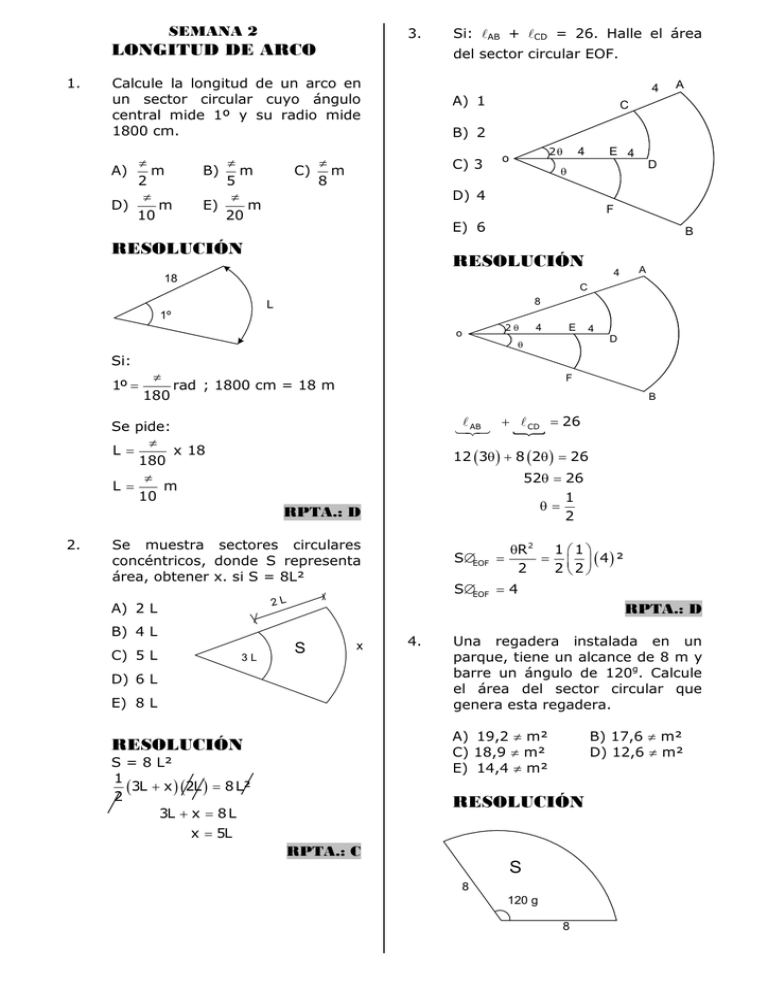
SEMANA 2 3. LONGITUD DE ARCO 1. del sector circular EOF. Calcule la longitud de un arco en un sector circular cuyo ángulo central mide 1º y su radio mide 1800 cm. π A) m 2 π D) m 10 π B) m 5 π E) m 20 Si: ℓAB + ℓCD = 26. Halle el área 4 A) 1 A C B) 2 π C) m 8 C) 3 E 4 4 2θ o D θ D) 4 F E) 6 RESOLUCIÓN B RESOLUCIÓN 4 18 A C 8 L 1º 2θ o 4 E 4 D θ Si: 1º = π rad ; 1800 cm = 18 m 180 F B ℓ AB Se pide: π L = x 18 180 π L = m 10 + ℓ CD = 26 12 (3θ ) + 8 (2θ ) = 26 52θ = 26 θ= RPTA.: D 2. Se muestra sectores circulares concéntricos, donde S representa área, obtener x. si S = 8L² S∆EOF = RPTA.: D B) 4 L C) 5 L 3L θR 2 1 1 = ( 4) ² 2 2 2 S∆EOF = 4 2L A) 2 L 1 2 S x D) 6 L E) 8 L 4. Una regadera instalada en un parque, tiene un alcance de 8 m y barre un ángulo de 120g. Calcule el área del sector circular que genera esta regadera. A) 19,2 π m² C) 18,9 π m² E) 14,4 π m² RESOLUCIÓN S = 8 L² 1 (3L + x ) (2L ) = 8 L² 2 3L + x = 8 L B) 17,6 π m² D) 12,6 π m² RESOLUCIÓN x = 5L RPTA.: C S 8 120 g 8 Si: 120g = 3π rad 5 RESOLUCIÓN Inicialmente: Se pide: 1 3π S= i i 8² 2 5 S = 19,2 π m² θrad S S= θR² 2 RPTA.: A Finalmente: 5. Si CAE es un sector circular y ED AB = BC. Halle : V = DC R + 5m= ? 4 θrad A 49 S A) 2 E B) 3 C) 4 B 49 S = 20º D) 5 ( 4θ ) (R + 5) ² 2 ↓ E) 6 D 49 i C θ R² 4θ (R + 5) ² = 2 2 RESOLUCIÓN 7R = 2 (R + 5) A R B R = 2m 60º 20º E R 20º ∴R + 5m = 7m RPTA.: D 80º D 80º C 7. Se pide: π iR V= 3 π iR 9 V=3 Halle el área sombreada: A A) π C B) 2 π C) 3 π RPTA.: B o 6 30º D) 4 π E) 5 π 6. Si a un sector circular le cuadruplicamos su ángulo central y aumentamos 5 m a su radio, se obtendrá un nuevo sector circular que tiene un área que es 49 veces el área del sector circular inicial. Determine el radio del nuevo sector. A) 2 m D) 7 m B) 3 m E) 9 m C) 5 m D B RESOLUCIÓN A a o C 6 30º b D B Sx = S∆AOB − S∆COD θ θ a² − b² 2 2 θ Sx = a² − b² 2 1π Sx = 6² 2 6 9. Sx = En la figura, el trapecio circular ABCD y el sector circular COD m tienen igual área. Halle: n A) 36π 12 Sx = 3π Sx = B) RPTA.: C C) Calcule: E = x³ − x² − 1, si: 8. A 2 2 D 1 2 2 C D) 2 A n m o B E) 1 x² C RESOLUCIÓN 5 x (x + 1) o x (x - 1) D A) 5 D) 8 B) 6 E) 9 B θrad C) 7 S S m n RESOLUCIÓN m² 2θ n² mayor : 2S = 2θ 1 m² = 2 n² menor : S = x² 5 θ x (x + 1) x (x - 1) 1 5θ = x ( x − 1) → θ = x ( x − 1) 5 2 = m → n ÷ m 2 = n 2 .........(1) RPTA.: A Luego : x − 1 x ( x + 1) = ( x² + 5 ) ( x ) 5 5(x+1) = (x²+5)(x−1) 5x + 5 = x³ − x² + 5x − 5 10 = x³ − x² ∴ E = x³ − x² − 1 E=9 RPTA.: E 10. Se tiene un sector circular y un cuadrado, con equivalente área e igual perímetro; luego la medida, en radianes, de su ángulo central correspondiente resulta ser: A) 1 rad B) 2 rad D) 4 rad E) 1 rad 4 C) 1 rad 2 RESOLUCIÓN RESOLUCIÓN R a C θ rad S o L θ x i) ii) S =S E Perímetro = Perímetro → → → 2R + L = 4a a y−x z−y = a 2a 2y − 2x = z − y 3y = 2x + z RPTA.: C a 12. a → → → → → F Luego: M = (3y) . y−1 ∴M=3 S a 2a De la figura: θ= z a Condiciones: L iR → = a² 2 → R.L = 2a² A y D R 2a B (2R+L)²=16a²→(2R+L)² = 8(2a²) 4R² + 4R.L + L² = 8(R.L) 4R² − 4R.L +L² = 0 (2R−L)² = 0 → 2R − L = 0 2R = L → 2R = θ R → θ = 2 RPTA.: B S2 + S3 S1 Donde S1, S2 y S3 son las áreas de las regiones sombreadas Calcule: M = S2 θ 2θ S1 S3 11. De la figura mostrada, AOF, BOE y COD son sectores circulares, además: 12 7 D) 5π + 2 13 2 E) 5π − 2 BC = DE = a, AB = EF = 2a, L CD = x, L BE = y, L AF = Z A) Calcule: M = (2x + z) y−1 RESOLUCIÓN E) 5 1 12 B C B) 2 D) 4 C) A A) 1 C) 3 B) o θ 2 θ S1 = 2S D S2 = 3S 6S S3. = 10S E F S1 = 2S S2 = 3S S3 = 10S M= S2 + S3 13 = S1 2 RPTA.: B 13. Dos postulantes de la UNAC, observan un reloj eléctrico cuyas agujas están detenidas, luego de la falla eléctrica en el Callao, uno de los estudiantes dice que el área que hacen las agujas es de 7,2 m² y si el reloj tiene un radio de 6 m. ¿Cuál será el arco entre las agujas? 22 Considere π = 7 12 11 A) mts B) mts 5 5 5 12 C) D) mts mts 12 7 5 E) mts 11 θ1 R 1 = θ2 R 2 αºR1 = (αg)R2 9 αºR1 = ( αº ) R2 10 R1 9 = R 2 10 RPTA.: C 15. Se tienen dos ruedas conectadas por una faja; si hacemos girar la faja, se observa que las ruedas giran ángulos que suman 144º. Determine la diferencia de los números de vueltas que dan estas ruedas si sus radios miden 3 m y 5m 1 1 1 B) C) A) 3 8 9 1 1 D) E) 4 10 RESOLUCIÓN S= 1 1 L R ⇒ 7,2 = L(6) 2 2 24 144 ⇒ = L(6) 10 L = RESOLUCIÓN θ1 + θ2 = 144º 5 12 mts 5 3 RPTA.: A 14. Se tiene una bicicleta cuyas ruedas tienen por radios R1 y R2 (R1 < R2); cuando la rueda menor gira αº la mayor gira αg. ¿En qué relación se encuentra los radios? 3 7 3 D) 10 A) 8 13 9 E) 4 B) C) 9 10 RESOLUCIÓN Si θ1 y θ2 son los ángulos que giran la rueda menor y mayor respectivamente. αg αº R2 R1 En una bicicleta se cumple que: → L1 = L2 → θ 1R 1 = θ 2R 2 θ1 R 2 V 5 = ⇒ 1 = θ2 R1 V2 3 θ1 θ 144π 1 + 2 = i 2π 2π 180 2π 2 2 V1 + V2 = ⇒ 8k = ⇒ V1 − V2 = 2k 5 5 1 1 k = V1 − V2 = 2i 20 20 1 = 10 RPTA.: E 16. En el sistema mostrado, si la 3 de vuelta, entonces rueda A da 4 la longitud recorrida por la rueda C es: 17. Determine el área de la región sombreada, sabiendo que las áreas de los sectores AOB y COD son iguales (α y θ en radianes) o α θ B R 8 2 6 A B A C D M A) 3,6 π B) 36 π 9π E) 4 D) 18 π C) 1,8 π C 1 R² ( α − θ ) 2 1 C) R² ( α² − θ²) 2 1 E) R² ( α − θ²) 2 RESOLUCIÓN A B 8 1 R² ( α + θ ) 2 1 D) R² ( α² − θ ) 2 B) A) 2 6 RESOLUCIÓN C 3 V 4 3 3π ⇒ θA = (2π rad) = rad 4 2 # VA = * 1 α r12 2 ⇒ αr12 = θR 22 R2 r1 S S S= 1 θR² 2 A − B: LA = LB θA RA = θBRB 3π 2 ( 6 ) = θB (2 ) θB = * S= α θ SX S + Sx = ST Sx = ST − S 1 1 Sx = αR² − αr12 Re emplazando 2 2 1 1 Sx = αR² − θR² 2 2 1 Sx = R² ( α − θ ) 2 9π 2 B − C: 9π 2 9π ∴ L C = θCR C = (8) = 36π 2 θB = θC = RPTA.: A RPTA.: B 18. Del gráfico, halle el número de vueltas que dará una ruedita de radio 1, al ir de A hasta B si CB = 8π y AOC es un sector circular. A o 5 RPTA.: D 20. De la figura mostrada, la rueda de radio r, gira sin resbalar sobre la superficie de radio 240 r. ¿Cuál es la longitud recorrida por el centro de la rueda hasta que el punto B este en contacto con la superficie de la curva, si: m ∢ AOB = 120º, r = 18u? B B C A) 2 D) 5 B) 3 E) 6 C) 4 r A RESOLUCIÓN A o B 4 L1 L2 C 8π 240 r B L1 + L2 = 2π (1) . N π i4 + 8π = 2πiN 2 10π = 2πiN N=5 A) 24 π B) 24,1π D) 24,3π E) 24,4π C) 24,2π RESOLUCIÓN RPTA.: D 19. A L AB = 240º π (18u) = 24π 180 Halle el número de vueltas que da la rueda de radio (r = 1) al ir de la posición A hasta la posición B. B r A 0 r L 24 20 o r A o B B r De la figura: A) 85 D) 10,5 B) 9 E) 11 C) 10 RESOLUCIÓN ℓ # V = RECORRIDA 2π r Sabemos: ℓr = (π) (21) = 21π ⇒ # vueltas = #v = 10,5 21 π 2 π (1) L 24π = 241r 240 r L = 24,1 π RPTA.: B 21. Sobre una superficie curva de radio “R” gira una rueda cuyo radio es “r” (ver figura). Si dicha rueda da una vuelta al ir de “M” a “N”. Calcule la longitud del arco MN. ( O y O′ son centros). la velocidad de A es a la velocidad de B como 3 es a 7. Calcule cuando mide “α” si se encuentran por 1era. vez en el punto R. A) B) r N o C) M R D) E) O′ A) R +r πRr E) πRr R +r 2πRr D) R +r R +r 2πRr P α Q RESOLUCIÓN Espacio recorrido por el móvil A será PR y del móvil B es el arco QR . eA = VAtA y eB = VBtB B) C) 2πRr (R + r ) π rad 5 R π rad 4 π rad 10 π rad 20 7π rad 10 Pero ambos parten tiempo tA = tB P al mismo RESOLUCIÓN π −α 2 R r α r θR r r Q r N r M ⇒ θRAD Reemplazando: Del gráfico: L 2πr n= ii) ℓ MN = θiR ∴ ℓ MN = →1= θ (R + r ) 2πr 2πr →θ= R +r 2πRr R +r RPTA.: D 22. 7eA = 3eB π eA = L PR = − α r y eB = L QR = ( π + α ) r 2 o i) eA V 3 = A = ⇒ eB VB 7 Dos móviles mismo tiempo indicadas en puntos P y Q A y B parten al y en las direcciones la figura de los respectivamente, si π 7 − α r = 3 (π + α)r 2 7π π − 7α = 3π + 3α ⇒ 10α = 2 2 π ⇒α= rad 20 RPTA.: D



